超滤法浓缩鳀鱼蒸煮液的数学模型

杨贤庆，周晓蕾,2，李来好，岑剑伟，郝淑贤，刁石强，魏 涯，石 红

超滤法浓缩鳀鱼蒸煮液的数学模型

杨贤庆1，周晓蕾1,2，李来好1，岑剑伟1，郝淑贤1，刁石强1，魏 涯1，石 红1

(1.中国水产科学研究院南海水产研究所，广东 广州 510300；2.上海海洋大学食品学院，上海 201306)

采用切向流超滤技术浓缩鳀鱼蒸煮废弃液中蛋白质，在前期对超滤压力、进样流速、样品pH值、操作温度等操作条件研究的基础上，建立超滤数学模型，通过实验获得拟合参数。结果表明：模型理论值曲线与实验值曲线拟合良好，各曲线的相关系数均在0.99左右，且膜通量理论值和实验值之间的误差较小，范围在0.44%～10.00%之间。在工业化设计和实践中，可以根据该数学模型预测超滤条件的变化对超滤过程的影响，根据该模型选择最佳的操作条件，有效地控制浓差极化和膜污染。

超滤；鳀；膜通量；数学模型

目前，世界水产品总产量已经超过1亿t，其中约30%的低值鱼类和下脚料被加工成低值产品，甚至部分被作为废物直接丢弃，这不仅造成资源浪费、降低产品附加值，而且还会对环境造成严重污染[1-3]。鳀(Engraulis japonicus)是一种高蛋白、高脂肪，集群性低值鱼类[4]。由于在蒸煮鳀鱼过程中，有大量的蛋白质、游离氨基酸等营养成分和风味物质会溶解在蒸煮液中。对这部分蒸煮液进行深加工，制成蛋白强化剂、调味品等具有很好的市场应用前景[5-6]。

超滤法具有多种优点，因此被广泛应用于食品、制药等领域，被普遍认为是生产食品级产品最具工业化前景的方法之一。在超滤过程中，影响分离效果的主要因素是浓差极化和膜的污染，它们会导致膜通量下降，无法进行长时间稳定操作。由于超滤的通量模型能够定量描述浓差极化及膜污染与各个操作因素之间的联系，以优化操作条件，获得长期稳定的膜通量，因此对其进行研究意义重大。目前，人们在超滤通量模型方面已经展开了全面的研究[7-11]。本实验在考察操作压力、温度等操作条件对超滤通量影响的实验基础上，建立描述鳀鱼蒸煮液超滤过程的数学模型。以期使用该模型预测鳀鱼蒸煮液在特定操作条件下的膜通量，从而有效地控制浓差极化和膜污染。

1 材料与方法

1.1 材料与试剂

鳀鱼加工蒸煮液由浙江瑞安市华盛水产品加工厂提供。浓硫酸、硼酸、氢氧化钠均为国产分析纯。

1.2 仪器与设备

Millipore LabscaleTMTFF System膜超滤装置、Pellicon XL Biomax 30超滤膜 美国密理博中国有限公司；kjeltecTM2300凯式定氮仪 瑞士福斯公司。

1.3 方法

1.3.1 鳀鱼加工蒸煮液超滤过程的控制

鳀鱼加工蒸煮液过0.2μm的微滤膜进行预处理，防止超滤膜的堵塞。在室温(30±1)℃条件下，控制超滤压力和进样流速，采用浓缩式操作方法对鳀鱼蒸煮液进行超滤浓缩，过程示意图如图1所示。当操作压力达到规定要求并稳定后，开始计时(t)，同时记录透过液的体积(V)。

图1 浓缩式超滤过程示意图Fig.1 Schematic diagram of ultrafiltration of Engraulis japonicus cooking soup

1.3.2 纯水膜通量的测定

在室温(30±1)℃条件下，进样流速为9.0L/h，控制操作压力，采用浓缩式操作方法对纯水进行超滤，过程示意图如图1所示。当操作压力达到规定要求并稳定后，开始计时(t)，同时记录透过纯水的体积V。

1.3.3 超滤压力的计算[12]

式中：ΔP为膜透压/MPa；Pin为物料进口压力/ MPa；Pout为回流液出口压力/MPa；Pp为透过液出口压力/MPa。

在该实验中，未在透过液出口设置阀门，因此Pp=0，故

1.3.4 超滤膜通量的计算[13]

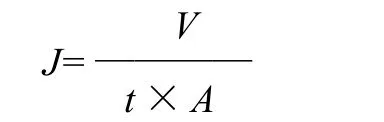
式中：J为超滤膜通量/(L/(m2·h))；t为取样时间/h；V为透过液体积/L；A为膜面积/m2。

1.3.5 蒸煮液中蛋白质含量的测定

采用凯式定氮法[14]。蛋白质的含量直接影响到膜表面的凝胶极化层和边界层的阻力，影响膜通量，因此实验前需对样品中蛋白质的含量进行准确测定。取样品液10.0～25.0mL(仪器检测限为0.1～200mg氮)至干净的消化管中，加入一片催化剂及20mL硫酸后，放于消化炉在420℃条件下消化50min。待消化完毕，温度降至200℃以下后取出消化管，放在室温中冷却至不烫手后拿到凯式定氮仪上进行测定，每组样品测3个平行。

1.3.6 模型参数计算

采用Matlab 7.1.0 Release 14 软件计算模型参数。

2 结果与分析

2.1 超滤模型的建立

该实验在较低的操作压力和蛋白质浓度下进行，且根据前期实验结果发现膜通量随操作压力的升高而增加[15]，故该实验采用阻力叠加模型[16]描述鳀鱼蒸煮液超滤过程中各个因素之间的关系。膜通量J可表示为：

式中：J为膜通量/(m3/(m2·s))；ΔP表示膜透压/ Pa；μ表示黏度/Pa·s；rm表示膜的阻力/m-1，它只与膜本身的性质有关；rg表示由于凝胶极化层产生的阻力/m-1，即凝胶层的渗透阻力；rbl表示由黏性-非凝胶的边界层产生的阻力/m-1。

各种阻力存在的形式见图2。

图2 超滤过程中的各种阻力存在形式Fig.2 Resistances during ultrafiltration

在建立模型时，作如下几点假设：

1)Rm=μrm，Rg=μrg，Rbl=μrbl，则：

2)在操作过程中温度保持恒定，温度变化对膜通量的影响忽略不计。

3)在操作过程中进样流速保持恒定，忽略进样流速变化对膜通量的影响。

4)当超滤纯水时，不产生浓差极化，不影响凝胶层，故Rg=Rbl=0。

5)当凝胶层存在时，随着超滤压力ΔP的增加，相应的凝胶层厚度也增加，导致凝胶层阻力也增大，故认为Rg与ΔP成正比， Rg=αΔP。故：

6)超滤过程中，Rg和Rbl受到进样流速v和鳀加工蒸煮液中蛋白质质量分数c影响，关系为α=Avacb，Rbl=Bvccd。故：

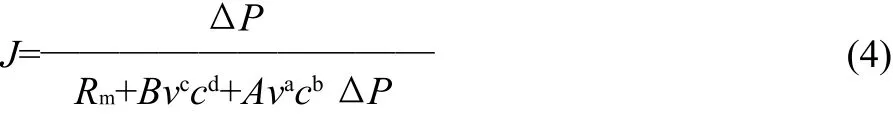
2.2 模型求解与参数估算

2.2.1 Rm的求解

Rm是膜本身的阻力，与物料的性质和操作条件无关，故在超滤纯水时，Rg=Rbl=0，即：

通过式(5)可以看出，通过测定不同压力下的纯水的膜通量可以求得Rm。以膜通量(J)为纵坐标，操作压力(ΔP)为横坐标，得到直线的斜率即为1/Rm，通过图3计算得Rm=0.000361m-1。

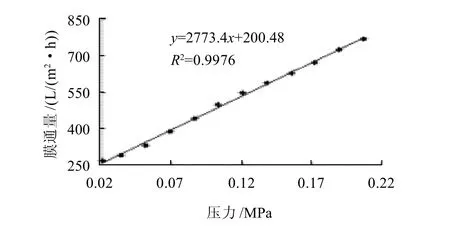
图3 超滤纯水时操作压力对膜通量的关系(T=30℃)Fig.3 Relationship between operating pressure and pure water flux

2.2.2 Rbl和Rg的求解

将Rm=0.000361m-1代入式(4)得式(6)：

将式(6)两边取倒数得：

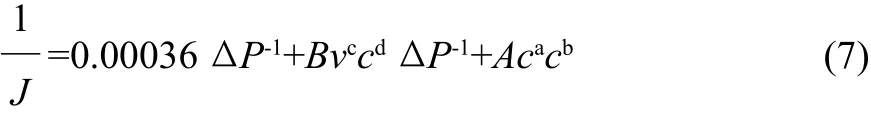
令J＇=1/J得：

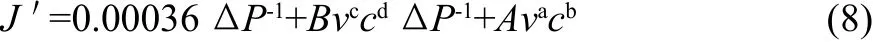
式中：J＇为函数；ΔP、v和c为自变量。采用Matlab 7.1.0 Release 14应用软件，根据实验测得的数据对方程(8)进行拟合，解出参数A、B、a、b、c、d，实验数据见表1。

表1 不同操作条件下的膜通量实验值和拟合值Table1 Experimental and predicted membrane flux under different operating conditions (varying permeate pressure and constant protein concentration and sample flow rate)

求解得到：A=0.0672，B=0.0225，a=－0.7564，b=0.4056，c=－0.7565，d=0.4055。将求得的参数代入式(6)，得到从鳀鱼蒸煮废弃液中浓缩蛋白质的超滤数学模型，即：

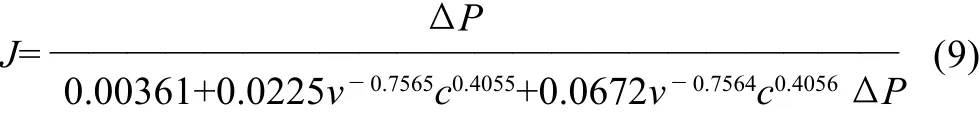
2.3 模型的检验

采用Matlab 7.1.0 Release统计软件，画出实验值曲线和拟合值曲线的图形，并计算其相关系数，对模型进行检验，结果见图4和表2。将实验值的拟合数据进行相对误差分析，以此对模型进行进一步检验，结果见表1。

图4 模型理论值和实验值的拟合Fig.4 Experimental and predicted relationships between membrane flux and permeate pressure at three constant levels of protein concentration and sample flow rate

表2 模型理论值和实验值的相关系数Table 2 Correlation coefficients between experimental and predicted membrane flux at three constant levels of protein concentration and sample flow rate

从图4可以看出，模型的拟合值和实验测量值具有良好的相关性，各条曲线的相关系数均在0.99左右。同时，从表1可以看出，膜通量的实验值和拟合值的相对误差为0.44%～10.00%，小于建模允许的误差15%，说明拟合值曲线和实验值曲线拟合程度较好。

2.4 模型的讨论

从模型中可以看出，Rm=0.000361m-1，较小，几乎可以忽略不计，说明改良的聚醚砜超滤膜表面性质良好，对蛋白质具有较弱的吸附力，有利于防止膜表面形成凝胶极化和污染。

Rg和Rbl均与进样流速v成反比，v越大越有利于切割掉膜表面的沉积层，以此减轻浓差极化和膜的污染程度；Rg和Rbl与样品中蛋白质质量分数成正比，样品中蛋白质浓度较高时容易在膜表面形成凝胶层，导致浓差极化现象。此结果与程坷伟等[17]得到的甘薯淀粉中糖蛋白的超滤数学模型结果一致。

当ΔP较小时，Rg可以忽略不计，膜通量就与ΔP成正比；当ΔP较大时，Rbl可以忽略不计，膜通量趋近于一个常数，此时的压力即为临界压力[18]。

由于在实验过程中，随着操作时间的延长，泵会产生热量，导致样品溶液的温度变化，并且由于仪器的限制，进样流速会有波动，这些原因都导致了膜通量的实验值与拟合值之间的轻微误差。

3 结 论

采用Matlab 7.1.0 Release统计软件，通过多元非线性回归的方法，建立了超滤法浓缩鳀鱼蒸煮液的数学模型为：

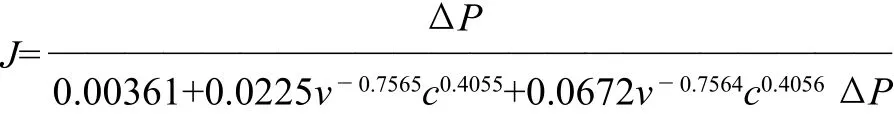
经检验，此模型的拟合值与实验值相对误差较小，在0.44%～10.00%范围内；拟合值和实验值具有较好的相关性，相关系数均在0.99左右，因此基本能准确估计不同操作条件下的膜通量。

此模型的建立，可以预测在不同的操作压力、进样流速、样品蛋白质质量分数下膜通量的变化，预测膜表面的污染和浓差极化程度，以此来获得稳定且较高的膜通量水平，为工业化规模生产提供有效的工艺参数，同时可对采用聚醚砜超滤膜设备提取蛋白质大分子物质提供一定的参考。

[1]白福玉, 郑华, 蒋爱民. 低值水产品及水产副产品的加工和综合利用[J]. 农产品加工, 2007(4): 76-79.

[2]齐凤生, 程秀荣, 张海莲. 海洋功能食品的开发与利用[J]. 水利渔业, 2002, 22(5): 28-30.

[3]黄东雨, 陈海光, KOW F. 海洋鱼类分割加工废弃物的综合利用[J].广东农业科学, 2009(9): 144-148.

[4]朱碧英, 冯旭文, 毋瑾超. 鳀鱼可溶性蛋白质及鱼油的开发[J]. 东海海洋, 2001, 19(2): 60-62.

[5]王文彬. 鱼类废弃物的加工与综合利用[J]. 渔业致富指南, 2006(19): 47-48.

[6]孙晓莲. 低值水产品及加工废弃物的综合利用[J]. 食品研究与开发, 2009, 30(3): 158-161.

[7]MONDOR M, GIRARD B, MORESOLI C. Modeling flux behavior for membrane filtration of apple juice[J]. Food Research International, 2000, 33(7): 539-548.

[8]MARCOS B, MORESOLI C, SKOREPOVA J, et al. CFD modeling of a transient hollow fiber ultrafiltration system for protein concentration[J]. Journal of Membrane Science, 2009, 337(1/2): 136-144.

[9]LUO Mingliang, PU Chunsheng, ZHAO Jianqing. Modeling on dynamic process of membrane fouling during finite crossflow ultrafiltration in charged system[J]. 水动力学研究与进展: B辑, 2006, 18(2): 206-210.

[10]MOHAMMADI T, KOHPEYMA A, SADRZADEH M. Mathematical modeling of flux decline in ultrafiltration[J]. Desalination, 2005, 184(1/ 3): 367-375.

[11]崔彦杰, 刘美, 王湛, 等. 超滤通量模型的研究进展[J]. 膜科学与技术, 2008, 28(6): 93-98.

[12]时钧, 袁权, 高从楷. 膜技术手册[M]. 北京: 化学工业出版社, 2001: 350-351.

[13]刘茉娥. 膜分离技术[M]. 北京: 化学工业出版社, 1998: 54-58.

[14]GB/T 5009.5—2003食品中蛋白质的测定[S].

[15]周晓蕾, 杨贤庆, 李来好, 等. 超滤法浓缩鳀加工蒸煮液的工艺研究[J]. 南方水产, 2010, 6(4): 26-31.

[16]王湛. 膜分离技术基础[M]. 北京: 化学工业出版社, 2006: 193-195; 198.

[17]程坷伟, 许时婴, 王璋. 甘薯淀粉生产废弃液中糖蛋白提取的超滤数学模型[J]. 无锡轻工大学学报, 2004, 23(6): 59-61.

[18]NOBLE R D, STERN S A. Membrane separation technology principles＆ applications[M]. Netherlands: Elsevier Science BV, 1995: 45-48.

Modeling for the Ultrafiltration Concentration of Engraulis japonicus Cooking Soup

YANG Xian-qing1，ZHOU Xiao-lei1,2，LI Lai-hao1，CEN Jian-wei1，HAO Shu-xian1，DIAO Shi-qiang1，WEI Ya1，SHI Hong1
(1. South China Sea Fisheries Research Institute, Chinese Academy of Fishery Sciences, Guangzhou 510300, China；2. College of Food Science and Technology, Shanghai Ocean University, Shanghai 201306, China)

In this work, tangential flow ultrafiltration was used to concentrate proteins in the cooking soup of Engraulis japonicus. Based on the studies on operating pressure and sample flow rate and pH, a mathematic model describing membrane flux as a function of permeate pressure, protein concentration and sample flow rate was established. The results showed that the predicted results of membrane flux as a function of permeate pressure at three constant levels of protein concentration and sample flow rate were in good agreement with the experimental results well, with a relative error varying between 0.44% and 10.00%, and the correlation coefficients were all around 0.99. Using this model in industrial design and practice, flux change can be predicted and optimal operating conditions can also be selected for solving the problems of concentration polarization and membrane pollution.

ultrafiltration；Engraulis japonicus；membrane flux；mathematical model

TS254.9

A

1002-6630(2010)19-0153-04

2010-06-30

国家“863”计划重点项目(2007AA091801)；“十一五”国家科技支撑计划项目(2008BAD94B08)

杨贤庆(1963—)，男，研究员，本科，主要从事水产品加工和质量安全研究。E-mail：yxqgd@163.com