一种化学气相淀积过程温度控制的新算法
2010-09-14袁德成
张 慧, 袁德成
(沈阳化工大学信息工程学院,辽宁沈阳 110142)
一种化学气相淀积过程温度控制的新算法
张 慧, 袁德成
(沈阳化工大学信息工程学院,辽宁沈阳 110142)
以化学气相淀积过程中晶圆表面温度分布为研究对象,分析反应过程中的工艺特点及动态特性,针对传统机理建模难以准确预测、控制晶圆表面温度的发展变化,提出基于线性二次优化的控制算法,由系统给定的输入及初始条件,计算出系统的响应来预测未来轨迹,通过仿真演示了控制器的控制性能.
化学气相淀积 ; 温度控制; 线性二次优化; 预测轨迹
集成电路是由多层被精细刻画过的薄膜组成,每层都用化学的方法改变其构造以达到期望的电子特性.尽管集成电路的设计一般由电子工程师来完成,但这些设计的制造要经过一系列的物理和化学操作单元来实现.主要的操作单元有清洗、光刻、离子注入、刻蚀、热处理、化学气相淀积(CVD),物理气相淀积、分子束外延、电镀、化学机械研磨、晶圆测试等,其中的一些过程都是在原子或分子级进行操作,任何一个环节出错,都会影响产品的质量.在芯片制造过程中,大部分所需的薄膜材料,不论是导体、半导体、或是介电材料,都可以用化学气相淀积来制备,它具有淀积温度低,薄膜成分和厚度易控,均匀性与重复性好,阶梯覆盖好,操作方便等优点.其中淀积温度低和覆盖性好对超大规模集成电路的制造十分有利,因此它是目前集成电路生产过程中最重要的薄膜淀积方法.目前最常用的方法有常压化学气相淀积、低压化学气相淀积以及等离子体增强化学气相淀积等.
化学气相淀积过程是一个非常复杂的非线性过程,其实质是指含有薄膜所需的原子或分子的化学物质在反应室内混合并在气态下发生反应,其原子或分子淀积在晶圆表面聚集,形成薄膜.淀积过程中反应炉内将发生 4种类型的化学反应,并伴随着低压,超真空,化学反应与传递现象同时发生等特点,反应炉内部的复杂性导致对其有效控制十分困难.长期以来,国内外研究人员针对化学气相淀积过程中的化学反应和传递现象,建立了多种数学模型及控制方法,其中主要有Middleman与 Hochberg从化学工程角度提出的不同建模方法[1];Badgwell等概括了 CVD过程的建模和控制问题[2];Edgar提出了基于模型的 run-to-run控制[3];以上提出的控制算法都是基于模型的控制算法,这些模型在理论上对于揭示反应炉内部的现象起到一定的积极作用,然而化学气相淀积过程参数多且过程复杂,很难建立精确的机理模型,在控制上呈现出一定的局限性.本文针对化学气相淀积过程中控制的难点,在分析CVD工艺和动态特性的基础上,求解温度分布动态模型,构造出数据平台,结合线性二次优化的控制算法,根据系统温度分布的真实输入及初始值,计算出系统的响应来预测系统的轨迹,取得了良好的控制效果.
1 CVD工艺简介及其数学模型
化学气相淀积是一个由气相物质传递 (通过对流和分子扩散)、均相或非均相化学反应以及热量传递组成的复杂系统.要获得具有一定化学组成、纯度高、结构完整、物理性能优良和均匀的薄膜,必须对淀积过程中的机理、特性及相互影响作深入研究.
化学气相淀积过程系统如图 1所示.以 H2与WF6发生的卤化还原反应为例,描述其工艺:晶圆被水平放置在石英托盘上,WF6通过墙上的狭缝中注入反应室,卤素灯在反应室的顶部透过石英窗给晶圆加热,H2与WF6在反应室内混合并在气态下发生反应,其原子或分子晶圆表面聚集,形成薄膜沉积在晶圆表面.其中温度是影响薄膜淀积速率,均匀性及平整性的重要参数,实验重点研究反应炉内的温度分布.

图1 CVD过程系统框图Fig.1 The schematic diagram of the CVD reactor chamber
为充分了解化学气相淀积特点,合理设计反应器结构,正确选择操作条件,研究人员对化学气相淀积过程的数学模型进行了大量研究.文献[4]中给出了化学气相淀积过程的模型推导过程,传热参数的选择以及反应堆的相关介绍.用能量守恒方程来描述 CVD过程的动态特性:

公式(1)中右边第一项代表位置方向上的热量传导,第二项表示晶圆表面与环境之间的热量传递,它的初始值为零.符号R表示保护环的半径,Rw表示晶圆半径.Qother表示所有热量传递的总和,它包括灯的热量Ql,晶圆和反应室温度交换Qc,以及晶圆和反应气体之间的热传递Qg,即

其中,加热灯的热量控制器u(t):0≤u(t)≤1.为获得晶圆表面温度的动态解,假设晶圆表面的初始温度为 300 K,加热灯的热量为 5 000 W/ m2,用MATLAB的 pdepe指令编写微分方程函数文件,初始条件函数文件,边界条件函数文件,求解(1)式中的偏微分方程,得到晶圆表面温度随时间t及位置x的分布情况,如图 2,图 3所示.采集 500组数据,构建数据平台,为控制器设计提供数据wd及初始条件.
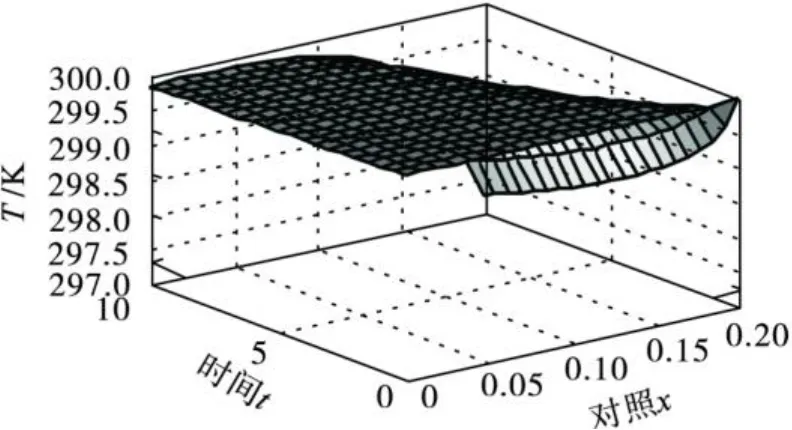
图 2 晶圆表面温度分布Fig.2 The temperature distribution at the wafer surface
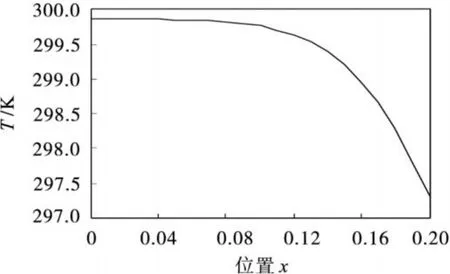
图 3 当u(t)从 1变为 0时温度与位置的关系Fig.3 Relationship of temperature and position whenu(t)changes from 1 to 0.
2 基于线性二次数据驱动的控制器设计
2.1 线性二次轨迹问题
首先介绍线性二次轨迹问题[5]:线性二次轨迹问题的目标是选择控制的输入,使对象B的最优轨迹服从二次误差准则:
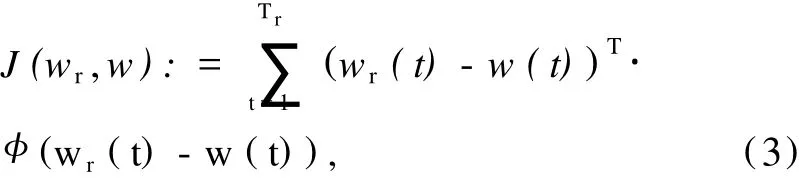
式中给定参考轨迹 wr∈,Φ∈,是一个正定加权矩阵,Tr是轨迹的范围.
给定条件如下:
(1)线性时不变系统 B的轨迹 wd= (wd(1),…,wd(T));
(2)参考轨迹 wr=(wr(1),…,wr(Tr));
(3) 初始轨迹 wini= (wint(1),…, wini(Tini))∈B;
找到对象 B的最优轨迹 w*∈B,使目标函数‖wr-w‖最小,即解决问题:

2.2 基于线性二次优化的温度控制
由采集的温度输入输出数据 wd=[u y],通过实现计算系统状态空间表达式的算法[5],辨识出系统的状态空间表达式参数 (A,B,C, D).计算系统的状态空间表达式[6]为:
输入:ud,yd,lmax,nmax.
1.计算出样本 nmax,lmax+1的自由响应 Y0;
2.将 Y0解为:Y0=ΓXd;
3.解出系统方程的状态空间表达式参数(A, B,C,D),其中[xd(1)…xd(nmax+m+1)]:=Xd.
输出:状态空间表达式参数 (A,B,C,D).一旦系统输入输出表达式的参数 (A,B,C, D)被确定,则由

两式可计算出系统的初始条件:

如果状态空间表达式及初始状态确定了,那么线性二次轨迹演变为解决如下的问题:


式(6)的解为

由式 (7)可计算出优化系统的温度:
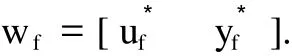
3 仿真结果与验证
被控对象晶圆温度系统阶次 n=2,输入m=1,输出 p=1,样本大小 N=200,参考轨迹wr=0,针对扰动大小为 ±25%的情况进行仿真.仿真结果如图 4所示,此时加热灯能量控制器u(t)=1.

图 4 晶圆表面温度分布(u(t)由 0变为 1)Fig.4 The temperature distribution on the w afer surface(u(t),from0to1)
将反应器内加热灯的能量控制器 u(t)由 1变为 0,仿真结果如图 5所示.

图 5 晶圆表面温度分布(u(t)由 1变为 0)Fig.5 The temperature distribution on the w afer surface(u(t),from1to0)
在时间 t=50s时,对系统加阶跃响应,仿真结果如图 6所示.由以上仿真结果可以看出,当系统存在扰动时,使用数据驱动控制算法计算出wf能够及时地控制及预测系统的未来轨迹,并能够计算出预测值 wf与真实数据 wd的误差仅为 0.019 4.针对以上分析可以看出,在系统存在扰动的情况下,基于数据驱动算法对于控制非常有效,同时具有很好的鲁棒性.

图 6 晶圆表面温度分布Fig.6 The temperature distribution on the wafer surface
4 结 论
基于线性二次优化的温度控制算法能够很好地反映晶圆表面温度分布的变化,能够及时跟踪温度的变化,具有很好的鲁棒性.针对化学气相淀积过程中控制的复杂性,传统的机理建模难以准确预测、控制晶圆表面温度的发展变化,基于线性二次优化的控制方法具有精度高,鲁棒性强等优点.目前研究的基于数据驱动的控制方法都是基于被控对象的轨迹是精确的,以及被控对象是低阶线性时不变系统的假设之下,而在实际生产中,系统是时变且有噪声的,因此获得数据驱动控制的优化算法是以后要研究的目标.
[1] H itchm an M L,Jensen K F.Chem ical Vapor Deposition—Principles and Application[M].N ew York: A cadem ic Press Inc.,1993:1300-1320.
[2] Badgwell T A,B reedijk T,Bushm an S G,et al. M odeling and Control of M icroelectronics M aterials Processing[J].Computers and Chem ical Engineering,1995:19(1):1-41.
[3] Edgar T F,CampbellW J,BodeC.M odel-based Control in M icroelectronics M anufacturing[J].Proceedings of the IEEE Conference on Decision and Control,2000,4:4185-4191.
[4] Chen J,Adomaitis R A.An Object-oriented Framework forM odular Chem ical Process Simulation with Sem iconductor Processing Applications[J].Computers and Chem ical Engineering,2006,30:1354-1380.
[5] M arkovsky Ivan,Rapisarda Paolo.On the L inear Quadratic Data-driven Control[C]//Proceedings of the European Control Conference.Kos:[s.n.],2007:5313-5318.
[6] M arkovsky Ivan,W illem s Jan C, Huffel Sanine V an,et al.Exact and Approx im ateM odeling of L inear System s:A Behavioral Approach[M].Leuven: M onographs onM athem aticalM odeling and Computation,2006:113-138.
[7] O verschee P V an,M oor Bart De.Subspace Identification for L inear System s:Theory,Implem entation, Applications[M].Boston:Kluw er academ ic publishers,1996:110-118.
[8] M arkovsky Ivan,W illem s Jan C,M oor Bart D e,A lgorithm s for Determ inistic Balanced Subspace Identification[J].A utom atica,2005,41(5):755-766.
A New Algorithm of Temperature Control for the Chem ical VaporDeposition Processes
ZHANG Hui, YUAN De-cheng
(Shenyang U niversity of Chem ical Technology,Shenyang110142,China)
The dynam ic characteristics of the chem ical vapor deposition process on affection of w afer’s temperature distributions are analyzed in this paper.It is difficult to predict and control the temperature of the w afer by the traditional m odeling approach.A linear quadratic optim al algorithm is presented,and the response of the temperature system is calculated by the given inputs and the initial condition in order to find the optim al trajectory of the system.The control perform ance is dem onstrated through s im ulation.
chem ical vapor deposition; temperature control; linear quadratic; optim al trajectory
TP273
A
1004-4639(2010)03-0275-04
2009-09-14
张慧(1985-),女,安徽黄山人,硕士研究生在读,主要从事基于统计的质量反馈控制系统的研究.
袁德成(1960-),男,内蒙古人,教授,博士,主要从事计算机辅助过程工程,生化过程建模与优化控制等方面的研究.
