自由边界条件下的温度梯度铁电薄膜的极化性质研究

陈 辉, 成泰民, 陈思群

(沈阳化工大学数理系,辽宁沈阳 110142)

自由边界条件下的温度梯度铁电薄膜的极化性质研究

陈 辉, 成泰民, 陈思群

(沈阳化工大学数理系,辽宁沈阳 110142)

在平均场近似下,采用横场 Ising模型研究自由边界条件下的温度梯度铁电薄膜的极化性质.当温度梯度铁电薄膜采用自由边界条件时,薄膜受热导致晶格沿极化方向膨胀使得赝自旋相互作用系数发生变化,因此,赝自旋相互作用系数应作为坐标的函数.研究表明:考虑赝自旋相互作用系数的变化后,温度梯度铁电薄膜的极化强度和相变温度都较不考虑赝自旋相互作用系数变化的情况有所增加.薄膜始末两赝自旋层的温度比以及薄膜固定端的温度是影响温度梯度铁电薄膜极化性质的两个重要因素.

温度梯度; 自发极化; 相变温度

梯度铁电薄膜材料是指铁电薄膜材料的某些特性参数(如组分、温度、应力等)沿与薄膜表面相垂直的方向呈连续变化或阶梯变化.由于梯度铁电材料的特性不同于非梯度铁电薄膜材料,以及它们在热释电探测器、传感器等方面的应用,关于梯度铁电材料的极化性能研究近年来引起了广泛关注[1-5].在这些研究当中,关于温度梯度铁电薄膜性质的研究很多,它们与极化偏移的“本源”问题[3],以及梯度铁电薄膜的热还原特性等有重要关联.

制备薄膜时,其性质很大程度上受外部因素的影响(电极、边界条件以及温度等),在不同的应用中铁电薄膜制备需要采用不同的边界条件.在实验研究中,温度梯度铁电薄膜可以采用不同的方法来制备.文献〔1〕中加热时采用紧密夹持在薄膜两侧的电极来制备温度梯度铁电薄膜,这种情况下为夹持边界条件,在这种边界条件下,铁电畸变引起的赝自旋相互作用系数的变化可以忽略[6].在文献〔5〕中,采用白炽灯照明加热的方法制备温度梯度膜,此时采用的是自由边界条件,薄膜受热膨胀导致的赝自旋相互作用的变化不能忽略[6].

理论上研究温度梯度铁电薄膜的方法主要有 GLD(Ginzburg-Landau-Devonshire)唯象理论和横场 Ising模型.而采用横场 Ising模型进行的研究中,理论模型大多为夹持边界条件[2-3],因为采用自由边界条件时,需要考虑赝自旋相互作用系数的变化,在计算上比较复杂.本文将建立自由边界条件的温度梯度铁电薄膜模型,引入分布函数描述赝自旋相互作用系数的变化,研究温度梯度铁电薄膜的极化性质.

1 理论模型

横场 Ising模型的哈密顿量可写为:

这里Ωi为横向场;和是坐标i处赝自旋的x和z分量;Jij是坐标i和j坐标两处两赝自旋相互作用系数,求和取遍所有坐标.

图 1为自由边界条件下,二级相变温度梯度铁电薄膜的理论模型.在薄膜内部存在着温度梯度,T1,T2,…,TN为每一赝自旋层的温度,假定薄膜的极化方向沿z方向,并垂直于薄膜表面,为了简化,假定横向场Ω在薄膜内部均匀分布,且只考虑相邻两赝自旋间相互作用.

图 1 自由边界条件下温度梯度铁电薄膜理论模型Fig.1 Model of temperature-graded ferroelectric film under free boundary condition

温度梯度铁电薄膜内部的赝自旋相互作用系数的变化十分复杂,它受到温度、热通量密度、热传导系数和样品厚度等诸多因素的影响.基于实验数据的参考,其分布函数可以写为[6]:

这里m是层序列号;N是薄膜的总层数;Fi(i= 2,4,6,…)是表征铁电畸变贡献的参数,在自由边界条件下,根据实验数据,可以取为F2=1.0 m4/C2,F4=10 m8/C4,F6=-100 m12/C6.计算中,忽略了Pm6次方以上的项,并且取Ω=J0.

参数a为薄膜内部第N层温度和第 1层温度之比,即:a=TN/T1,这里取均匀的温度梯度,

第m层的极化强度可以表示为:

n是单位体积内含有赝自旋的个数,μ是极化偶极矩的大小.

平均极化强度可以表示为:

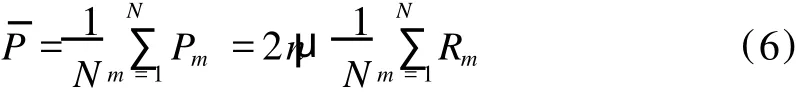
2 数值计算结果与讨论

下面就自由边界条件下温度梯度铁电薄膜的极化性质进行理论研究.图 2为考虑与不考虑赝自旋相互作用系数变化两种情况下,薄膜内部的极化强度分布曲线.参数N=10,a=0.2.对比图 2中两曲线,可以看到考虑了赝自旋相互作用系数变化后,薄膜极化强度增大.这是因为薄膜内部受热膨胀后,沿着自发极化方向晶格常数增加,导致赝自旋相互作用系数增加,这是极化强度增大的原因.

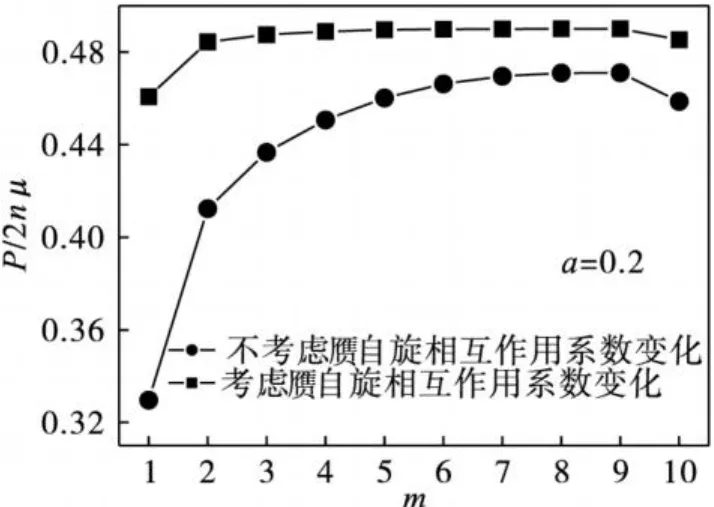
图 2 对比赝自旋相互作用系数是否变化两种情况下,温度梯度铁电薄膜内部的极化分布曲线Fig.2 Polarization distribution in temperature-graded ferroelectric film in cases of considering or non-considering the variation of pseudo-spin interaction couplings

参数a为薄膜内部第N层与第 1层温度的比值,当a<1时,第N层的温度低于第 1层的温度;当a>1时,第N层的温度高于第 1层的温度.在制备温度梯度铁电薄膜的过程中,通常固定薄膜一端的温度,改变另 1端的温度,以此在薄膜内部产生温度梯度.在此固定薄膜第 1层温度t1=KBT1/J0=1.0,由此,作出了图 3和图4,分别为a<1和a>1两种情况.在图中可以看到,由于温度梯度以及赝自旋相互作用系数梯度的存在,极化梯度的大小和方向与施加在温度梯度薄膜上的温度梯度及赝自旋相互作用梯度的大小和方向有关.对于表征薄膜内部温度梯度的参数a,尽管温度梯度是均匀的,但极化梯度是不均匀的.如图 3所示,a<1,整个薄膜的极化分布随层数的增加而连续增加 (第 10层突然降低是由于赝自旋配位数为 5,小于第 9层赝自旋配位数 6,故突然降低);并且随着参数a的增加,极化变化得越陡峭.图 4对应a>1的情况,呈现了与图 3相反的趋势,随着层数的增加,极化强度逐渐减小.当温度梯度较大时 (a=1.8),温度梯度膜的最外层即将变为顺电相,当温度梯度进一步增大,变为顺电相的层数将越来越多.

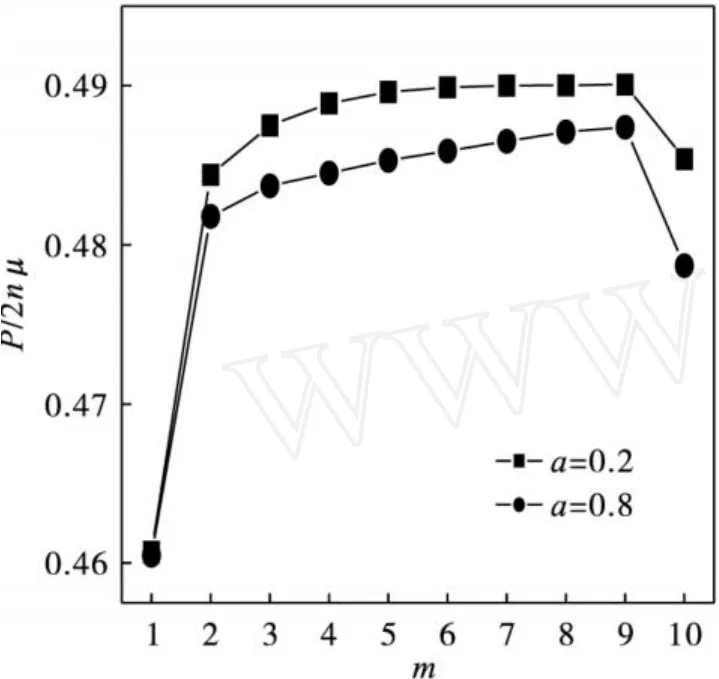
图 3a<1时薄膜内部极化分布曲线Fig.3 Polarization distribution in fi lm in case ofa<1

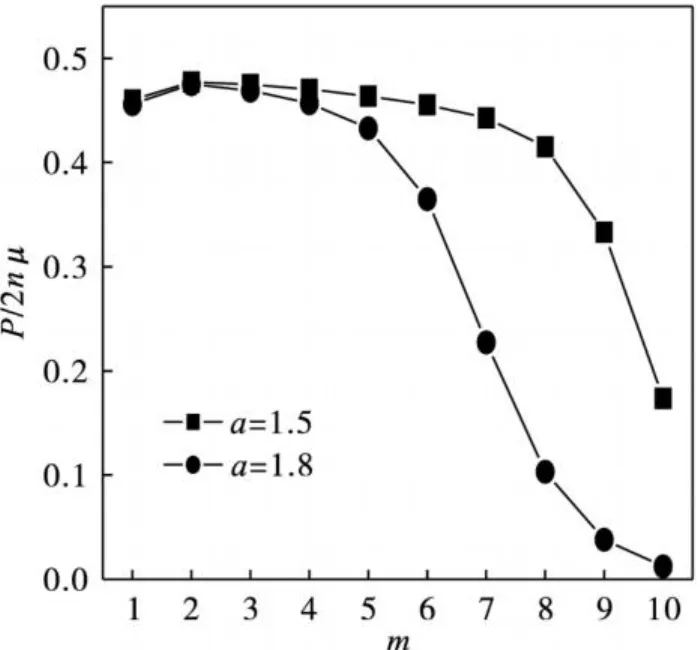
图 4a>1时薄膜内部极化分布曲线Fig.4 Polarization distribution in fi lm in case ofa>1

图 5和图 6分别为平均极化强度与第 1层温度T1及参数a的关系曲线.从图 5中可以看到:增加薄膜固定端的温度T1,平均极化强度逐渐降低,随着参数a的逐渐增加,平均极化强度和相变温度都在逐渐降低.图 6中,变化参数a的取值,对于给定的温度T1,当a<1时,随着a值的增大,温度梯度减小;当a>1时,随着a值的增大,温度梯度也增大,也就是参数a单调增加过程中,经历了温度梯度的减小和增大两个过程,而薄膜的平均极化强度却是随着参数a的增加而单调降低的.

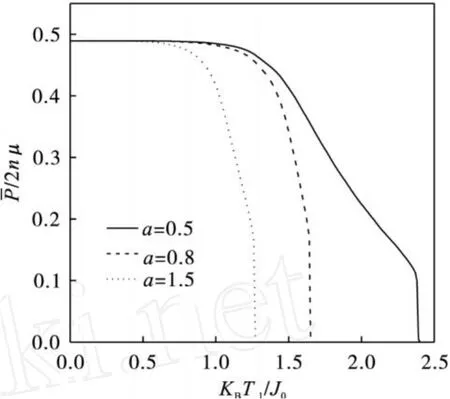
图 5 平均极化强度与温度T1之间关系曲线Fig.5 Mean polarization as a function ofT1

图 6 平均极化强度与参数a关系曲线Fig.6 Mean polarization as a function ofa

3 结 论

在平均场近似下,采用横场 Ising模型理论,研究了自由边界条件下的温度梯度铁电薄膜的极化性质.引入分布函数描述赝自旋相互作用系数的变化.研究表明:自由边界条件下的温度梯度铁电薄膜,考虑赝自旋相互作用系数的变化后,极化强度和相变温度都较不考虑赝自旋相互作用系数变化的情况有所增加.参数a和薄膜固定端的温度T1是影响薄膜极化性质的两个重要参数,它们的增加将降低薄膜的平均极化强度.

[1] Fellberg W,M antese J,Schubring N,et al.O rigin of the“up”,“down”Hysteresis O ffsets O bserved from Polarization-graded Ferroelectric M aterials[J].Appl.Phys.Lett.,2001,78(4):524-526.

[2] A lpay A P,Ban Z G,M antese J V.Therm odynam ic analysis of temperature-graded Ferroelectrics[J]. Appl.Phys.Lett.,2003,82(8):1269-1271.

[3] W ang X S,W ang C L,Zhong W L,et al.Polarization and dielectric Properties of Temperature-raded Ferroelectric Structure from theTransverse Ising M odel[J].M ater.Sci.Eng.B,2003,99:576-579.

[4] Cao H X,Lo V C,L i Z Y.D ielectric Response of Temperature-graded Ferroelectric Film s[J].J.Appl.Phys.,2005,98:114105-1-114105-6.

[5] Bogom olov A A,M alyshkina O V,Solnyshkin A V. Effects of Temperature Gradient on Surface Dom ain Structure in DTGS Crystals[J].Ferroelectrics, 1997,191:313-317.

[6] Zhang L,Zhong W L,Kleem ann W.A Study of the Q uantum Effect in BaT iO3[J].Phys.Lett.A,2000, 276:162-166.

Plarization Properties of Temperature-graded Ferroelectric Fi lm s under Free Boundary Condition

CHEN Hui, CHENG Tai-m in, CHEN Si-qun
(Shenyang U niversity of Chem ical Technology,Shenyang110142,China)

In the fram ew ork of the m ean field approxim ation,a transverse Ising m odel(T IM)is adopted to analyze the polarization properties of temperature-graded ferroelectric film s under free boundary condition.W hen temperature-graded ferroelectric film s are under free boundary condition,due to the expansion along the polarization aroused by heating,pseudo-spins interaction couplings get changing.Hence,the interaction couplings should be considered as a function of coordinate.The results show that considering the variation of pseudo-spins interaction couplings,polarization and phase-transition temperature becom e larger.The temperature of top layer and the ratio betw een the top-layer temperature and bottom-layer temperature are the tw o important factors that influence the polarization properties of temperature-graded ferroelectric film s.

temperature gradient; spontaneous polarization; phase-transition temperature

O482.4

A

1004-4639(2010)03-0279-04

2009-12-23

国家自然科学基金资助项目(10647138);辽宁省科研基金资助项目(20060667)

陈辉(1979-),女,吉林吉林人,讲师,博士,主要从事低维凝聚态体系的研究.