三次B样条反求控制点
2010-09-14王凌云
王凌云
(山东服装职业学院科研所,山东泰安 271000)
三次B样条反求控制点
王凌云
(山东服装职业学院科研所,山东泰安 271000)
反求工程作为复杂工业产品设计与制造的重要技术手段之一,深受CAD/CAM领域的广泛重视,特别是自由曲面重构技术作为复杂曲面产品反求工程中的“瓶颈”问题,是今后一个时期的研究热点.反求工程中最为关键的技术就是曲面重构技术.目前主要有两大重构方法:NURBS曲面重构和三角Bezier曲面重构.本文围绕NURBS曲面重构展开研究,提出一种反算三次B样条曲线、曲面控制顶点的简便算法.该算法适用于准均匀和非均匀B样条曲线、曲面的反算.算法采用非节点边界条件,不需要由用户提供,从而使反算过程得以简化.
反求工程;非均匀有理B样条;型值点;控制点
0 引言
在CACG实践中,常遇到要求构造插值曲线和插值曲面,以用于已有曲线曲面的形状表示.NURBS方法为标准解析形式的初等曲线曲面和自由型曲线曲面的精确表示和设计提供了一个公共的数学表示,有操纵控制顶点及权因子,为各种形状设计提供了充分的灵活性,由于非均匀有理B样条(NURBS)可以精确表示解析形状和自由曲线曲面,国际标准组织于1991年把NURBS作为表示工业产品几何形状的工业标准.
NURBS曲线曲面在实际应用中可以分为两种形式:一种是已知控制点求解曲线曲面上的点,称为正算问题.另一种情况是已知曲线曲面上的型值点,求解曲线曲面的控制点,称为反算问题.在实际应用中,常常是给出一组离散的型值点,要求构造通过该型值点的曲线曲面,即所谓的曲线曲面插值.文中只讨论三次NURBS曲线问题,给出反算控制点的方法.
1 反算三次B样条插值曲线的控制顶点
1.1 B样条基础知识
B样条方法是以距离加权插值法为基础,以数据点为型值点反求其控制点,然后将B样条曲面看作是两个不同方向的B样条曲线的直积,避免复杂的矩阵运算.B条曲面由于其本身具有的跨界曲率自连续性使得曲面片间的光顺性问题得以简化.
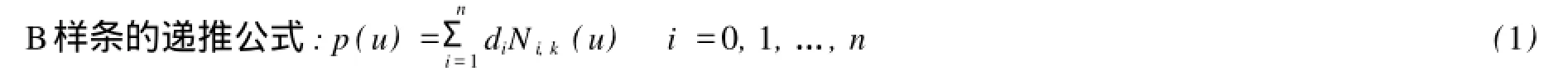
其中di(i=0,1,…,n)为控制顶点,又成为德布尔点,顺序连成的折线又称为B样条控制多边形, Ni,k(u)(i=0,1,…,n)称为规范k次B样条基函数,是由节点矢量U=[u0,u1,…,un+k+1]按Cox-De Boor递推公式定义的k次规范B样条基函数,表示如下:
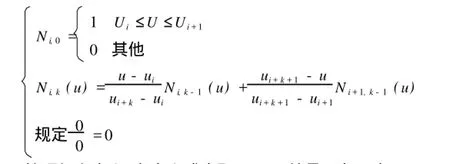
按照如上定义,在定义式中取k=3就是一条三次NURBS曲线的数学表达式.一般常用的是非均匀有理B样条,它采用非均匀节点矢量,并在两端点处采用重节点技术,使得曲线严格地插值于首末端点,工程中,一般三次B样条曲线曲面己经能满足实际的需求了.
1.2 B样条曲线反算的一般过程
a)根据型值点的分布趋势,构造非均匀节点矢量. b)应用计算得到的节点矢量构造非均匀B样条基. c)构建控制点反算的系数矩阵.
d)建立控制点反算方程组,求解控制点列.其中,B样条基函数的求值是关键.
1.2.1 假设规定
为使一k次B样条曲线通过一组数据点qi(i=0,1,…,m),反算过程一般地使曲线的首末端点分别和首末数据点一致,使曲线的分段连接点分别依次与B样条曲线定义域内的节点一一对应.即qi点有节点值uk+i(i=0,1,…,m).
1.2.2 三次B样条插值曲线节点矢量的确定
曲线控制点反算时一般使曲线的首末端点分别与首末型值点一致,型值点pi(i=0,1,…,n)将依次与三次NURBS曲线定义域内的节点一一对应.三次NURBS插值曲线将由n+3个控制点di(i= 0,1,…,n+2)定义,相应的节点矢量为U=[u0,u1,…,un+6].为确定与型值点相对应的参数值ui+3(i=0,1,…,n),需对型值点进行参数化处理.选择ui一般采取以下方法:
(1)均匀参数化法:
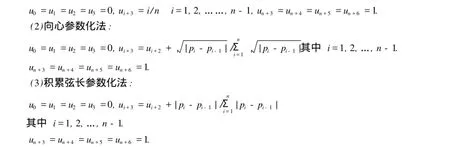
1.2.3 反算三次B样条曲线的控制顶点
给定n+1个数据点pi,i=0,1,…,n.通常的算法是将首末数据点p0和pn分别作为三次B样条插值曲线的首末端点,把内部数据点p1,p2,…,pn-1依次作为三次B样条插值曲线的分段连接点,则曲线为n段.因此,所求的三次B样条插值曲线的控制顶点bi,i=0,1,…,n+2应为n+3个.节点矢量U=[u0,u1,…,un+6],曲线定义域u∈[u3,un+3].B样条表达式是一个分段的矢函数,并且由于B样条的局部支撑性,一段三次B样条曲线只受4个控制点的影响,下式表示了一段B样条曲线的一个起始点:
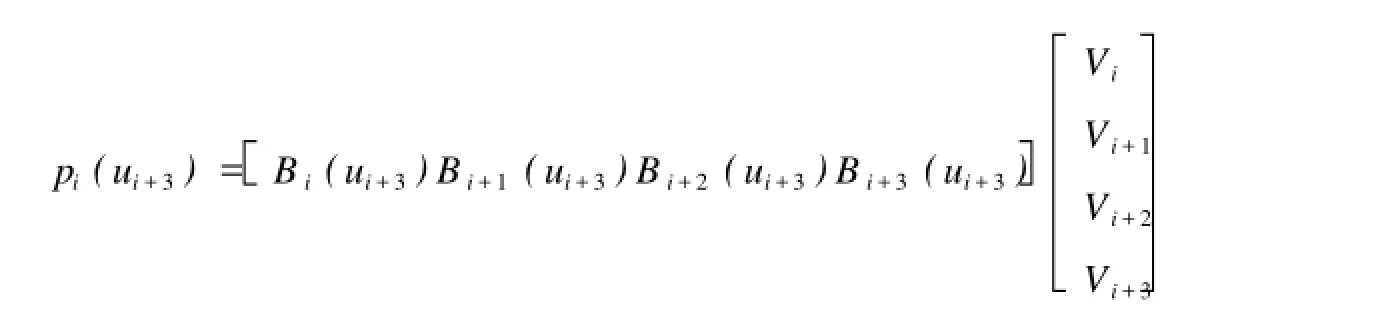
式中ui+3为起始点的参数值,i∈[0,m-4],通过该式可获得m-3个分段曲线的起始点.由于采用了重节点技术,末端型值点与控制点重合,则p0=V0;pm-3=Vm-1.则反求控制点方程组如下:
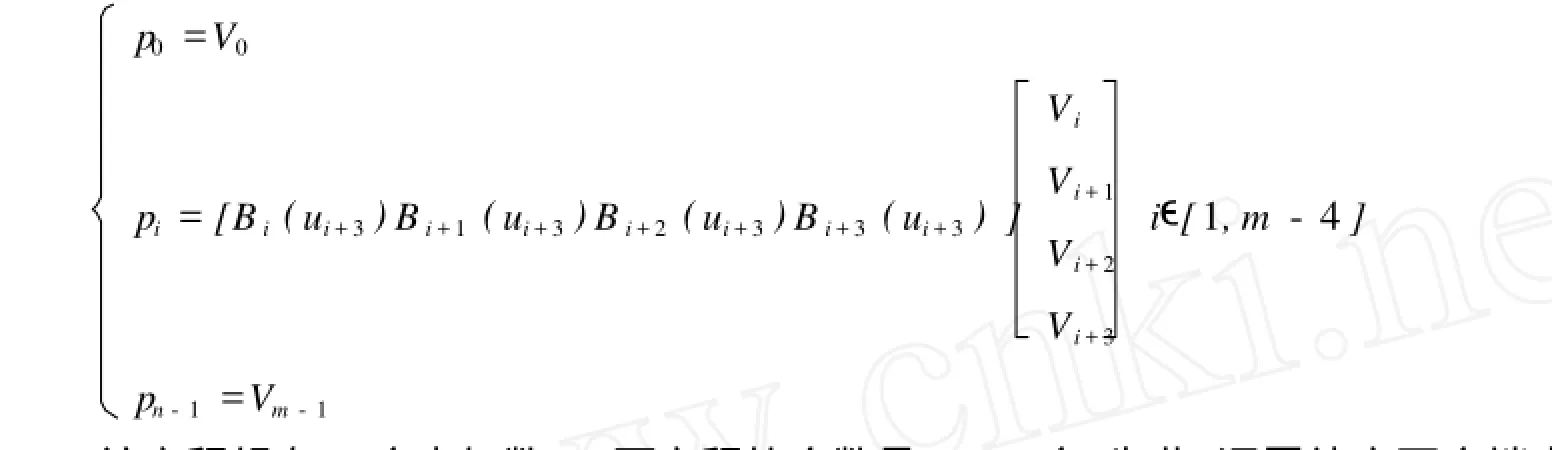
该方程组有m个未知数Vj,而方程的个数是m-2个.为此,还需补充两个端点条件:对于C2连续的三次B样条闭曲线,因为首末数据点相重,q0=qm,不计重复,方程减少一个,又首末三个控制点依次相重,即dn-2=d0,dn-1=d0,dn=d2;未知控制点的数目减少了三个,所以方程个数与未知数个数相同,上述线性方程组可改写成如下矩阵形式,
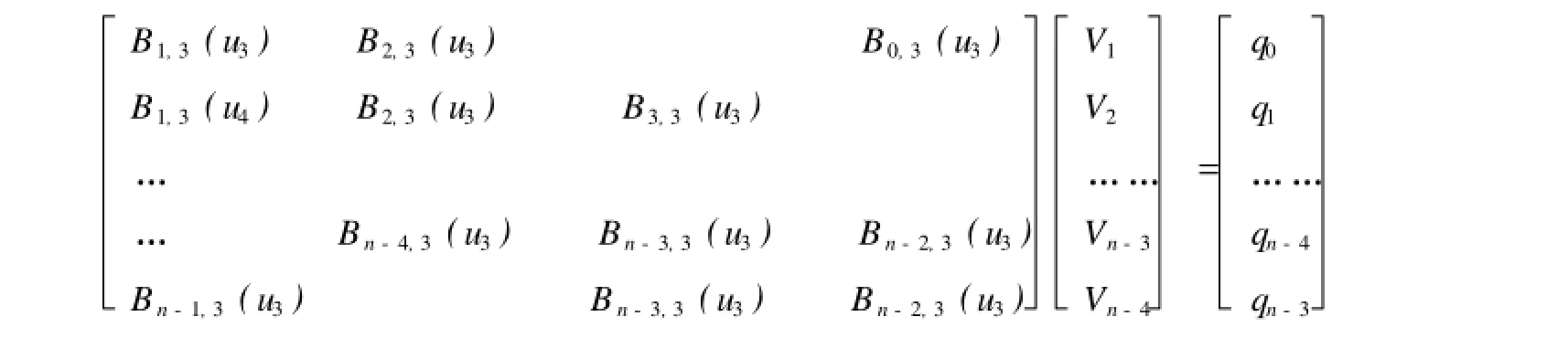
解方程,即可求出全部控制点.
对于B样条开曲线以及不要求在相重的首末数据点q0=qm处C2连续的三次B样条B曲线,n-1个方程不足以决定其包含的n+1个未知控制顶点,还必须增加两个通常由边界条件给定的附加方程,这样求解三次B样条控制顶点的线性方程组可以写成如下矩阵形式.
2 B样条曲面的重构
2.1 B样条曲面重构
对于B样条曲面的重构,实际上就是已知型值点Qij(i=0,1,…,m;j=0,1,…,n);求相应均匀双三次B样条曲面的控制点阵pij(i=-1,0,1,…,m+1;j=-1,0,1,…,n+1)具体的方法就是:
1)对u向的n+1组型值点,按照B样条曲线的边界条件及反算公式,求得由n+1组B样条曲线构成的控制多边形,这里每条曲线均要加两个边界条件,故会得到(m+3)*(n+1)个特征网格控制点Vij(i=-1,0,1,…,m+1;j=-1,0,1,…,n+1).
2)把Vij看作是v向的(m+3)次B样条曲线反算,即可得到双三次B样条曲面的控制点pij(i=-1,0, 1,…,m+1;j=-1,0,1,…,n+1).如果从0开始算点,pij(i=0,1,…,m+2;j=0,1,…,n+2).
2.2 插值曲面的光顺性问题
利用上述方法得到的曲面,在片内满足C2连续,但在片间的公共边界以及多个片相交的角点处,只满足了位置连续,需要进行光顺处理.
光顺方法大体上可以分为两大类:局部光顺法和整体光顺法.局部光顺法只是对少数“坏点”进行修改,具有较强的局部修改能力,并且计算速度快,但是“坏点”较多时光顺的效果不理想;整体光顺法是对全部型值点进行修改,曲面整体光顺效果较为理想,但计算量大,收敛速度慢.光照反射特性法属于整体光顺法,通过反射线来检查曲面的光顺性.能量法是典型的整体光顺法,使曲面的整体能量在一定的约束条件下达到最小.但是用能量法光顺曲面,不论原来的曲面是什么形状,光顺后的曲面趋于向平面变化,导致曲面变形,而且计算速度受控制顶点个数的限制,不适合处理大量数据.小波分析法是将曲面分解为低分辨率曲面和细节曲面,分解次数越多,曲面越光顺.分解算法和重构算法速度快,适合大数据量曲面光顺.无论采用哪种方法,要达到所有截面曲线和控制曲线都光顺不是轻而易举的,要求设计员拥有相当的经验积累和理论基础,经过耐心细致艰巨的工作才能实现.
曲面的光顺问题迄今没有得到圆满的解决,人们期待在这方面得到突破性的进展.
3 结论
在反算控制点过程中,用的参数化方法不同,最后的结果也有差别,比较而言采用积累弦长参数化法最合适.均匀参数化方法比较适合于数据点多边形各边接近相等的场合.积累弦长参数化法如实反映了数据点按弦长的分布情况,一直被认为是最佳参数化法.它克服了数据点按弦长分布不均匀情况下采用均匀参数化所出现的问题.向心参数化方法考虑了数据点相邻弦线的折拐情况,当数据点有急剧拐弯时,这种方法效果很好.所以,在实际应用中要根据数据点的分布情况选择合适的参数化方法来反算控制点.本文给出了一种反算三次B样条插值曲线和双三次B样条插值曲面控制顶点的简便算法.其实践证明:该算法稳定可靠,速度较快,结果也能令人满意.当用户对边界条件无特殊要求时,适合采用本算法.
[1]王飞.三次B样条反算的一种简便算法[J].北京邮电大学学报,1996,(3):84-90.
[2]施法中.计算机辅助几何设计与非均匀有理B样条[M].北京:北京航空航天大学出版社,1994.
[3]吕丹,等.三次NURBS曲线控制点的计算[J].弹箭与制导学报,2006,(4):357-359.
[4]彭伟.逆向工程中的NURBS曲面重构研究[D].南京:南京理工大学,2003.
[5]徐文鹏.基于人体特征的服装cad参数化技术研究与应用[D].杭州:浙江大学,2004.
[6]王少纯,等.基于NURBS方法的三维型腔曲面的几何描述及网格域的生成[J].哈尔滨工业大学学报,2000,32(2).
[7]杨晓静.B样条曲面构造方法的研究和实现[D].北京:北京工业大学,2003.
Ca lcula ting Con trol Poin tsof NURBS
WANG Ling-yun
(Institute of Scien tific Research,Shandong Fashion College,Tai’an,271000,China)
Reverse engineering(RE)is a key techno logy of advancedm anufac tu ring.A sone of im po rtan t technicalways to design andm anufacture comp lex industrialp roducts,reverse engineering is taken into a accountw idely in the field of CAD/CAM.Especially,free-form surface reconstruction is a challenging task andw ill catchmore attention in futurewo rk.Surface reconstruction is themost important techno logy in RE. There are two p revailing su rface reconstruc tionm ethods.They are NURBS su rface reconstruc tionm ethod and triangle surface reconstructionm ethod.This thesism akes som e researchwork on NURBS surface reconstruction.Our paper p roposed a simp lem ethod which can calcu late the contro l points in NURBS curves and surfaces.This arithm etic app lies to quasi-unifo rm B-sp line and non-unifo rm B-sp line.The arithm etic uses non-node boundary cond itions and does no t need in terac tion,w hich can simp lify the operation p rocess.
reverse engineering;non-unifo rm B-sp line;characteristic point;con tro lpoints
TP301.6
A
1672-2590(2010)03-0040-04
2010-04-06
王凌云(1970-),女,山东泰安人,山东服装职业学院科研所讲师.
