RTT变位模式下考虑位移影响的被动侧土压力的计算与分析

杨泰华,贺怀建,俞 晓

(1.武汉科技大学城市建设学院,湖北武汉,430070;2.中国科学院武汉岩土力学研究所,湖北武汉,430071)

RTT变位模式下考虑位移影响的被动侧土压力的计算与分析

杨泰华1,2,贺怀建2,俞 晓1

(1.武汉科技大学城市建设学院,湖北武汉,430070;2.中国科学院武汉岩土力学研究所,湖北武汉,430071)

采用位移土压力计算理论,结合室内模型实测值对RTT变位模式下考虑位移影响的被动侧土压力进行计算与分析。结果表明,土压力强度沿墙高度的分布、土压力合力大小以及合力作用点的位置均与实测值基本相符合,说明在RTT变位模式下采用计算理论公式计算被动侧土压力是可行的;与n=0.78时相比,n= 0时符合更好,这可能与模型箱尺寸效应以及试验箱上部土体受到扰动较大有关;随着 n值的逐渐增大,土体更易达到朗肯被动极限状态。

RTT;变位模式;位移效应;土压力

目前,在土压力计算工程中,采用的方法是朗肯土压力理论和库伦土压力理论。由于墙体变位模式和位移的大小对挡土墙土压力分布有着很大的影响[1-5],因此采用该方法计算被动土压力时常出现计算值与实测值的误差,有时甚至相差几倍。为解决计算工程中的实际问题,国内外学者对不同变位模式下考虑位移影响的土压力计算理论进行了大量研究。Chang[6]和蒋波[7]等假定填土内摩擦角和该点土体位移呈线性关系,分别对绕墙脚转动(RB模式)和墙体平移(T模式)下的非极限主动土压力进行了计算;徐日庆[8]等根据墙体平移对墙后填土内摩擦角及墙土接触面上外摩擦角的影响,建立了内外摩擦角与位移之间的关系式;章瑞文[9]等通过对每一土层的不同墙面、滑裂面摩擦角和计算参数的分析,提出了挡土墙主动土压力的逐层计算方法;马文国[10]等将填土内摩擦角和墙面外摩擦角与墙体绕墙底向外转动角之间的关系引入改进的传统水平层分析法中,用于求解挡土墙绕墙底转动模式非极限状态下的主动土压力。但对考虑变位模式情况下的被动侧位移土压力的研究少见报道。为此,本文采用位移土压力计算理论,假定内摩擦角与位移呈非线性关系,结合室内模型实测值对RTT(绕墙顶上某点转动)变位模式下考虑位移影响的被动侧土压力进行计算,并将其变位模式下的土压力计算值与实测值进行对比分析,以期为RTT变位模式下被动土压力的计算工程提供实用性依据。

1 计算方法

考虑位移效应的土压力计算模式[11]为

式中:kφ、kc分别为角度折减系数和黏聚力折减系数;γ为土体重度,kN/m3;z为土体深度,m;c为计算土体黏聚力,kN/m2;φ为内摩擦角,(°)。

式中:A1、A2、B、x0分别为待定系数,均与墙土之间的外摩擦角δ和土体内摩擦角φ有关(B>0); x为挡土墙发生的相对位移量x=s/H,其中,H为挡土墙高,s为挡土墙发生的实际位移量,取向土体方向位移为正。

式中:i=a、p,向着(或背着)土体位移取p(或a); kc>1时,取1;kc<-1时,取-1;p为与位移s相对应的土压力强度,kPa。

考虑位移效应的土压力计算模式具有有界性,符合极限状态下的初值条件,且能够将主动(被动)土压力强度随着位移变化连续地表达出来;能够考虑挡土墙背与土体之间外摩擦角的影响等特性。具体特性描述见文献[11]。

2 算例分析

挡土墙的位移模式主要有墙体平移(T模式)、绕墙顶转动(RT模式)和绕墙底(RB模式)转动。绕墙顶转动和绕墙底转动还可演变为更具代表性的绕墙顶上某点转动(RTT模式)和绕墙底下某点转动(RBT模式),如图1所示(图中 n为转动点至墙顶距离与支护桩墙高 H之比)。

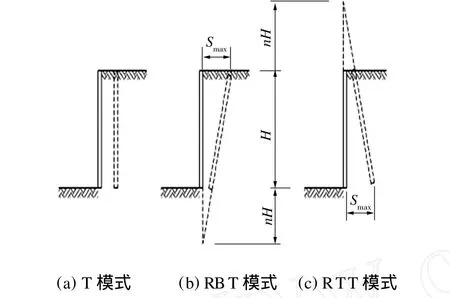
图1 被动状态下的变位模式Fig.1 Models of movement in the passive state

在模型试验中,与 T模式变位下的实验数据[3]进行对比分析,其主要参数[3]有:实际干容重为15.642 kN/m3;砂土内摩擦角为34.2°;墙土间外摩擦角为22.8°。对T模式变位下的土压力实测值进行反演分析后,求得计算值为:A1= -1.070,A2=1.561,x0=0.011 23,B=0.013 44。

2.1 被动土压力强度的分布

在RTT变位模式下,即绕墙顶以上某点转动,分别取n=0和 n=0.78两种情形进行分析,水平土压力沿深度方向的分布如图2所示。由图2可看出,挡土墙在RTT变位模式下,土压力沿墙高方向土压力强度的分布均具有一定的非线性特征,当n=0时,墙上土压力强度呈较明显的凹抛物线分布,即墙顶部和墙中部值较小,墙底部值最大。从土压力的发展速度来看,挡土墙上部土压力发展速度较为缓慢,挡土墙下部土压力发展速度非常迅速。这与本文所提出的土压力计算理论公式的分布特征相吻合。从土压力强度的数值大小来看,挡土墙上中部土压力的计算值和实测值相吻合,下部土压力计算值和实测值较为接近,但挡土墙中下部土压力的计算值比实测值相差稍大。从整体上来看,挡土墙在RTT模式下的土压力强度沿墙高方向分布的计算值与实测值基本相符合。

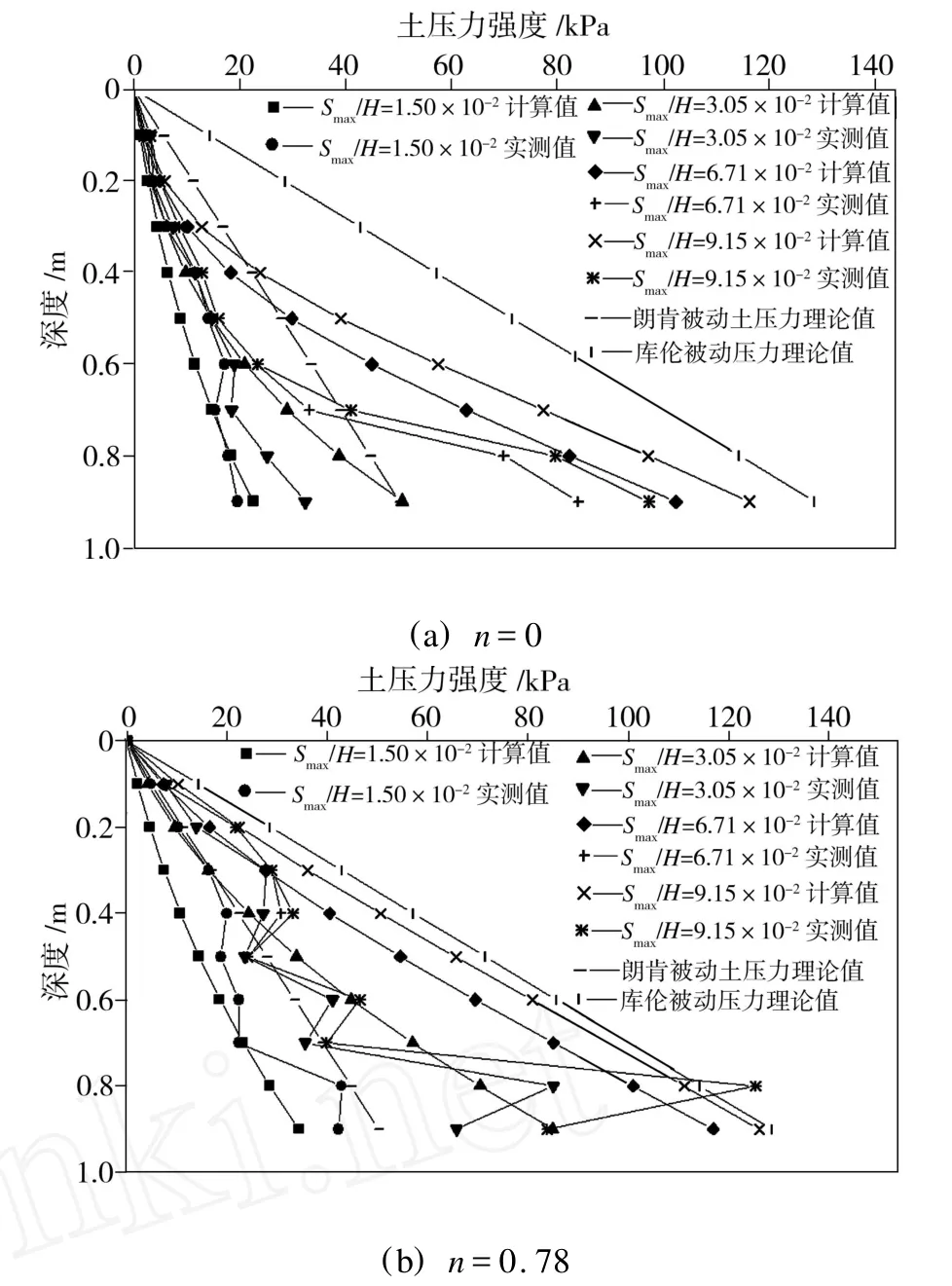
图2 RTT变位模式下被动土压力计算值与实测值对比Fig.2 Calculated and measured passive earth pressures at RTTmodel

2.2 土压力合力大小和作用点位置

在RTT变位模式下 ,分别取n=0和n= 0.78两种情形的土压力合力大小以及作用点的位置进行对比(见表1),当最大位移值较小时,挡土墙上土压力合力的实测值较计算值大,而随着底部位移值的逐步增大,计算值会逐渐赶上并超过实测值。从土压力合力的计算值与实测值的吻合程度来看,与n=0.78时相比,尤其是当墙底部位移值较大时,n=0时吻合更好。从土压力合力作用点的位置来看,RTT变位模式下土压力合力作用点位置的实测值和计算值几乎都在1/3 H以下,并且n=0时合力作用点的位置普遍比n= 0.78时的位置更靠近墙底。从达到朗肯被动土压力理论值所需要的最大位移量来看,当 n=0时 ,Smax约为0.06 H;当n=0.78时 ,Smax约为0.04 H,因此在相同的给定条件下,n值越大,越易达到朗肯被动极限状态。另外,从土压力合力和合力作用点的整体情况来看,其计算值与实测值也基本相符合。

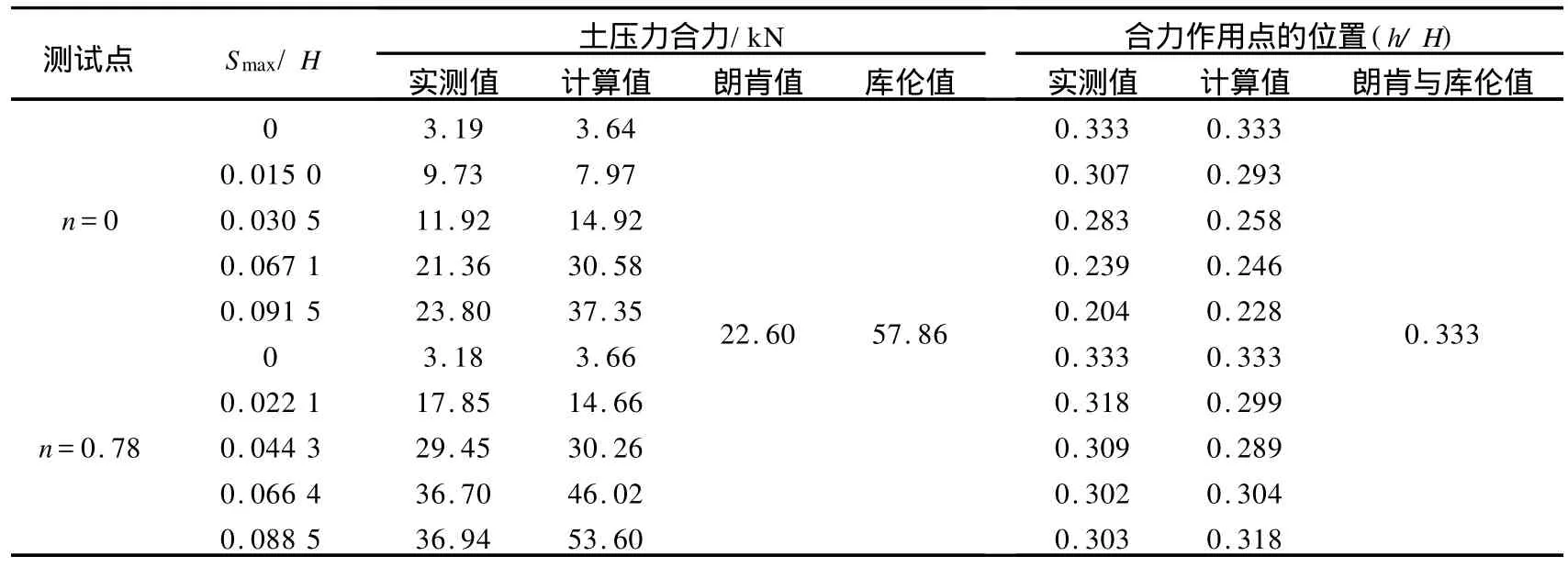
表1 RTT模式下土压力合力大小及合力作用点位置实测值与计算值Table 1 Calculated and measured joint forcesand itsaction points of earth pressuresat RTTmodel

3 结论

(1)采用笔者提出的土压力计算模式计算挡土墙上被动侧土压力,其计算结果在土压力强度沿墙高度的分布、土压力合力大小以及合力作用点的位置等三方面与实测值相吻合,表明在RTT变位模式下采用此计算理论公式计算被动侧土压力是可行的。

(2)在RTT变位模式下,从三方面的实测值吻合情况来看,与 n=0.78时相比,尤其是当墙底部位移值较大时,n=0时符合更好,这可能与模型箱尺寸效应以及试验箱上部土体受到扰动较大有关,从而使土压力的实测值降低。

(3)从达到朗肯被动土压力所需的最大位移Smax来看,随着 n值的增大,Smax值会逐渐减小,且随着n值的逐渐增大,土体更易达到朗肯被动极限状态。cal Engineering,1986,112(3):317-333.

[3] 徐日庆,陈页开,杨仲轩,等.刚性挡墙被动土压力模型试验研究[J].岩土工程学报,2002,24(5): 569-575.

[4] Ichihara M,Matsuzawa H.Earth p ressure during earthquake[J].Soils and Foundations,1973,13 (40):75-86.

[5] Sherif M A,Ishibashi I,Lee C D.Earth p ressures against rigid retaining walls[J].Journalof Geotechnical Engineering,1982,108(5):679-695.

[6] Chang M F,Lateral earth p ressure behind rotating wall[J].Canadian Geotechnical Journal,1997,34 (2):498-509.

[7] 蒋波,应宏伟,谢康和,等.平动模式下挡土墙非极限状态主动土压力计算[J].中国公路学报,2005, 18(2):24-27.

[8] 徐日庆,龚慈.考虑平动位移效应的刚性挡土墙土压力理论[J].浙江大学学报:工学版,2005,39(1): 119-122.

[9] 章瑞文,徐日庆,郭印.挡土墙主动土压力的逐层计算法[J].岩土力学,2006,27(S):151-155.

[10]马文国,孔亮,王燕昌,等.挡土墙绕墙底转动下非极限主动土压力的研究[J].宁夏大学学报:自然科学版,2007,28(4):330-333.

[11]杨泰华,贺怀建.黏性土基于强度折减法的位移土压力理论[J].岩土力学,2009,30(S2):185-188.

[1] Bang S.Active earth p ressure behind retaining walls [J].Journal of Geotechnical Engineering,1985,111 (3):407-412.

[2] Fang Y S,Ishibashi I.Static earth p ressure w ith variouswallmovements[J].Journal of Geotechni-

Calculation and analysis of passive earth pressure in themodel of RTTmovement with displacement effect considered

Yang Taihua1,2,He H uaijian2,Yu Xiao1
(1.College of City Construction,W uhan University of Science and Technology,W uhan 430065,China; 2.Wuhan Institute of Rock and Soil Mechanics,Chinese Academy of Sciences,Wuhan 430071,China)

Based on the earth p ressure theory,an indoor model experiment was carried out to calculate and analyze the passive earth p ressure acting on the retaining w all in the model of RTT movement w ith disp lacement taken into account.The analysis show s that the calculated values and the test values agree w ith each other well in the distribution of earth p ressure along the wall height,the valuesof the total earth p ressure,and the location of the action point of the total earth p ressure.This suggests,it is feasible to use the calculation model to calculate the passive earth p ressure in themodel of RTT movement.Comparatively speaking,w hen n=0 the calculated values aremo re identical w ith the test values than w hen n=0.78,w hich may be relevant to the size effect of the box of the model test and the fact that the upper soilof the box of themodel is disturbed more greatly.In addition,w ith the value of n increasing gradually,the soil is easier to reach Rankine’s passive limit state.

RTT;movement model;disp lacement effect;earth p ressure

TU 413.6

A

1674-3644(2010)06-0656-04

[责任编辑 徐前进]

2010-05-10

湖北省教育厅科研资助项目(2003A 001);武汉科技大学校青年科研基金资助项目(2006XY8).

杨泰华(1976-),男,武汉科技大学讲师,中国科学院武汉岩土力学研究所博士生.E-mail:yth001009147@163.com

贺怀建(1956-),男,中国科学院武汉岩土力学研究所研究员,博士生导师.E-mail:hjhe@w hrsm.ac.cn