一种基于MA TLAB的钢材裂纹扩展速率试验数据处理方法

刘建亮,岳应娟

(第二炮兵工程学院,陕西西安,710025)

一种基于MA TLAB的钢材裂纹扩展速率试验数据处理方法

刘建亮,岳应娟

(第二炮兵工程学院,陕西西安,710025)

提出一种基于 MATLAB软件设计的钢材裂纹扩展速率试验数据处理程序,并利用该程序对18M nMoNb钢和16MnR钢裂纹扩展速率试验数据进行处理。在分析程序运行结果的基础上,评价七点递增法、五点递增法、三点递增法针对不同试验数据处理精度的优劣性,并分析Paris公式中常数 C、m的相关性,得出了C、m的相关性经验公式。

MA TLAB;裂纹扩展速率;试验数据处理程序;递增法

1 问题的提出

疲劳裂纹的扩展大致可以分为3个阶段[1],如图1所示。在第一阶段内,裂纹前沿应力场强度因子幅ΔK值较低,裂纹扩展速率d a/d N(a为裂纹长度;N为载荷循环次数)也较低,当ΔK低于疲劳裂纹扩展的临界应力场强度范围因子幅,即应力门槛值ΔKth时,d a/d N=0,裂纹基本上不扩展。第二阶段是疲劳裂纹扩展的稳定阶段,也是决定疲劳寿命的主要阶段。一般认为,在双对数坐标系中,该阶段d a/d N与ΔK的关系是一条直线。用于描述这一阶段的d a/d N的关系式有数十个,其中用得最广泛而且最简单的是 Paris提出的表达式[1]:

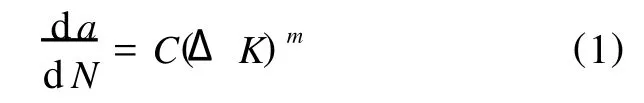
式(1)中,C、m是与试验条件如环境、温度、频率、应力比等有关的材料常数,可由标准的疲劳小试样获得,在概率断裂力学的计算中,C、m常视为随机变量,不少文献认为ln C与m具有相关

图1 ln(d a/d N)与lnΔK的关系曲线Fig.1 Relationship between ln(d a/d N)and lnΔK

性[2-3]。

在双对数坐标系中,式(1)的形式为

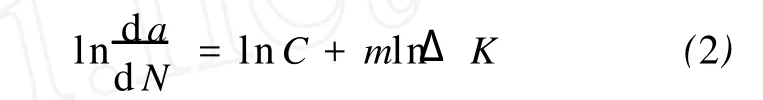
若ΔK继续增大,则进入疲劳裂纹扩展第三阶段,这时最大循环应力 Kmax已接近材料的平面应变断裂韧度 K1C,随着裂纹的扩展,ΔK亦迅速增大并导致材料失稳断裂。与裂纹扩展第一阶段一样,第三阶段仅占疲劳寿命极少部分。

由此可见,在材料的疲劳分析中,第二阶段的分析是关键。有多种方法测定材料的d a/d N,具体方法可以参照文献[4]。该阶段疲劳分析的基本思路:按照标准设计裂纹扩展速率试验,测得(ai,Ni),求得(d a/d N)i和ΔKi,最后对(d a/ d N)i和ΔKi做幂乘回归,即可求得材料常数 C和m。

要获得可靠的材料常数C和m,首先要在试验中提高测量精度,其次就是要有一个精确的试验数据处理模型。本文给出了一种基于MA TLAB的裂纹扩展速率试验数据处理方法,并利用该方法对18M nMoNb钢和16M nR钢裂纹扩展速率试验数据进行处理。试验所用试样皆为三点弯曲试样。试样1为18M nMoNb钢,试样厚度B =38 mm,试样宽度W=80 mm,试验载荷范围ΔP=5 000 kg;试样2为16M nR钢,B=8 mm,W=16 mm,ΔP=451 kg。

2 程序设计及数据处理

要把由试验测得的(ai,Ni)数据由头到尾采用多项式法精确拟合比较复杂。但是如果把a-N曲线分割成多个小区间,在每个小区间上,用一个简单的二次多项式就可以得到很好的拟合结果。可以采用这样的分割方法:从第1个点到第(2n+ 1)个点为第一区间,从第2个点到第(2n+2)个点为第二区间,…,从第 x个点到第(2n+x)个点为第 x区间。当n分别取1、2、3时,对应的拟合方法分别称为三点递增法、五点递增法和七点递增法。这样,对每个区间采用最小二乘法的原理进行拟合,就能得到很好的局部拟合方程,求出(d a/d N)i,按照疲劳分析的基本思路即可获得最后结果。

图2以七点递增法为例,给出了MA TLAB软件[5-6]设计的计算程序框图。

其他递增法改变图2中相关程序参数即可。

图2 MATLAB计算程序框图Fig.2 Flow chart of the processing based on MATLAB

3 结果与分析

试样1和试样2数据分别经不同拟合方法拟合后得出的d a/d N值和可决系数R2的值如表1所示。

可决系数为模型所描述的数据的变化率,该值越接近1,模型越有效。从表1中可以看出,对于试样1,两种对应方法处理结果可靠性都很高;对于试样2,五点递增法和三点递增法可靠性明显高于七点递增法,这是因为试样2试验数据为8组[7],如果按照七点递增法拟合只能分为两个区间,这种拟合方法不能很好地反应数据的变化规律,因此可靠性就不如其他两种方法,而试样1数据为34组[7],数据相对较多,用七点递增法拟合就能达到较高的拟合精度。

图3为18M nMoNb钢和16M nR钢两种试样裂纹扩展速率试验的 a-N数据点图。由图3中可见,随着循环周次N的增大,裂纹长度a也逐渐增大,且a的变化速率呈上升趋势。

表1 试样的d a/d N和R2值Table 1 d a/d N and R2values of samples

采用不同的递增法对试样的裂纹扩展速率试验数据进行处理,结果如图4所示。从图4中可以看出,试样1采用七点递增法时获得的拟合曲线比较光滑,而试样2采用三点递增法时获得的‘拟合曲线比较光滑。

图3 裂纹扩展a-N数据点Fig.3 The a-N points for crack propagation

图4 不同递增法拟合结果比较Fig.4 Comparision between different incrementalmethods

图5 95%置信度拟合值置信区间Fig.5 Confidence interval of fitted value at 95%confidence level

图5所示为16M nR钢裂纹扩展速率试验结果在不同拟合方法下对应的95%置信度拟合值置信区间。从图5中可以看出,同样是95%置信度的拟合值置信区间,同一试样的可决系数越接近1,区间的宽度越窄,这表明拟合模型的可靠性越高。

图6为ln(d a/d N)i与lnΔKi一元线性回归拟合结果的残差累积分布图。拟合结果残差服从正态分布的可能性越强,拟合模型的可靠性越好。从图6中可以看出,对于本文所涉及的两种试样,对其相应的ln(d a/d N)i与lnΔKi采用一元线性回归模型进行拟合是可靠的。

将对试样2数据处理结果(见表1)中得到的3对C、m值与文献[7]中所得的试样2的两对C、m值组成5对数据组,求得ln C的值,并进行拟合,结果如图7所示。从图7(a)中可以看出,数据点近似在一条直线上。对这些数据进行一元线性回归拟合,假设其模型为

图6 一元线性回归模型拟合结果的残差正态累积分布图Fig.6 Normal probability plot of the fitted values for one-dimensional linear regression model

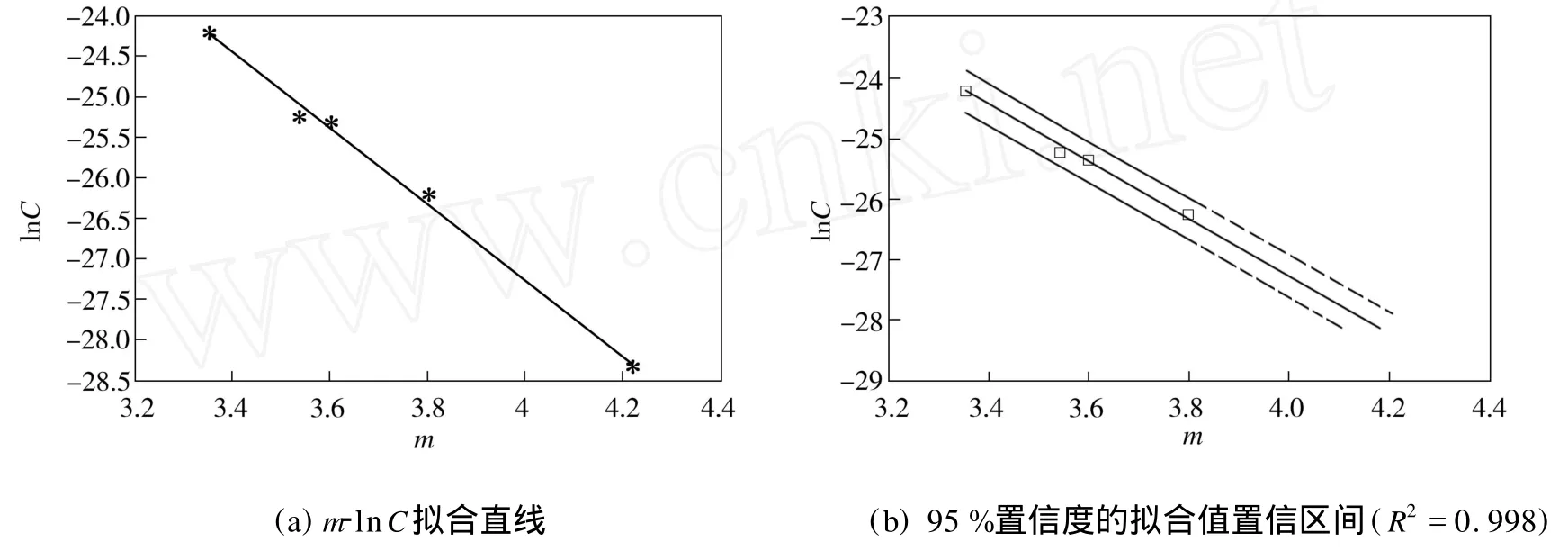
图7 试样2的m-ln C拟合结果及其95%置信度的拟合值置信区间Fig.7 The m-ln C fitted valuesand its conf indence interval at 95%confidence level

式中:A、B为拟合后的回归系数。

拟合后可求得A=-4.728 3,B=-8.373 8,该模型的可决系数 R2=0.998。这证实了文献[2]、文献[3]所提及的材料常数C、m的相关性。

4 结论

(1)基于MA TLAB的钢材裂纹扩展速率试验数据处理方法克服了逐个输入测量数据的繁琐性。对ln(d a/d N)i与lnΔKi采用一元线性回归模型进行拟合是可靠的。

(2)对于裂纹扩展稳定阶段,在载荷条件不变的情况下,裂纹扩展速率随着循环周次的增加逐步增大。在试验测量数据较少时运用三点递增法或五点递增法模型可以得到比七点递增法模型更高的精度,试验数据较多时用七点递增法可得到可靠度较高的结果。递增法分段拟合曲线的光滑性与最后的拟合结果的可靠性有直接的关系。

(3)C、m数据分析验证了ln C与m的相关性。16M nR钢材料常数C、m的相关性经验公式为ln C=-4.728 3m-8.373 8,可决系数R2= 0.998。

[1] 赵建生.断裂力学及断裂物理[M].武汉:华中科技大学出版社,2003:2.

[2] 周则恭.概率断裂力学在压力容器中的应用[M].北京:中国石化出版社,1996:76-98.

[3] 陈国华.疲劳裂纹随机扩展规律分析方法[J].南京化工大学学报,1996,18(3):63-66.

[4] GB/T 20120—2006.金属和合金的腐蚀—腐蚀疲劳试验[S].

[5] 张圣勤.MA TLAB7.0实用教程[M].北京:机械工业出版社,2006:3.

[6] Edward B Magrab,Shapour Azam,James H Duncan,等.MA TLAB原理与工程应用[M].高会生,李新叶,胡智奇,等译.北京:电子工业出版社,2002:6.

[7] 王印培.d a/d N试验数据的一种处理方法[J].化工与通用机械,1983(12):38-41.

A MATLAB-based method for processing test data of steel crack propagation rate

L iu Jianliang,Yue Yingjuan
(The Second A rtillery Engineering College,Xi’an 710025,China)

The paper introduces a M A TLAB-based p rogram designed to p rocess the test data of steel crack p ropagation rate.The p roposed p rogram was used to handle the test data of the crack p ropagation rate of 18M nMoNb steel and 16M nR steel,and the result w as analyzed.On this basis,the p recision of seven-point,five-point and three-point incremental methods in p rocessing different types of test data was evaluated.The pertinency of constants C and m in Paris formula was analyzed,and the empirical formula about C and m was given.

M A TLAB;crack p ropagation rate;test data p rocessing p rogram;incremental method

TG405

A

1674-3644(2010)06-0590-05

[责任编辑 郑淑芳]

2010-04-01

刘建亮(1984-),男,第二炮兵工程学院硕士生.E-mail:chenfengsuibi@sohu.com

岳应娟(1972-),女,第二炮兵工程学院副教授.E-mail:yingjuanyue@163.com