双馈电机调速系统的仿真研究

李 岚,刘艳丽

(太原理工大学电气与动力工程学院,太原030024)

近十年来,随着电力电子技术、微电子技术以及现代控制理论的发展,电气传动技术领域已出现交流电机调速取代直流电机调速的发展趋势。对于一些高电压、大功率且调速范围不大的应用场合,采用绕线型异步电机双馈矢量控制系统(简称双馈电机矢量控制系统),具有装置可靠性高、造价低廉、动态响应快、谐波污染小等特点,因此应用前景广阔。

双馈的主要优点在于能把转差功率馈送到电网中去,或由电网馈入,或高效地利用它,使相应的调速系统具有良好的性能。双馈调速工作时,除了电机定子侧与交流电网直接连接外,转子侧也要与交流电网或外接电动势相连。从电路拓扑结构看,可认为是在转子绕组回路中附加一个交流电动势[1]。

笔者采用定子磁链定向的矢量控制方法,建立了定子磁链的电流模型。在MATLAB/Simulink环境下,构建了双馈电机控制系统的速度和电流双闭环仿真模型。并在次同步速、超同步及负载发生变化时的情况进行仿真,分析不同运行状态下的转速、定子电流、转子电流及电磁转矩的变化。

1 数学模型

根据电机学理论,双馈电机可通过转子侧串入交流电压进行调速,当双馈电机负载转矩不变的情况下,转子电流保持不变,这时调节转子外加交流电压的频率、大小和相位,既可以调节转差率,达到调速的目的,又可以调节双馈电机的功率因数。

在d、q坐标系下,双馈电机数学模型如下[1]：定、转子电压方程

定、转子磁链方程

电磁转矩方程

运动方程

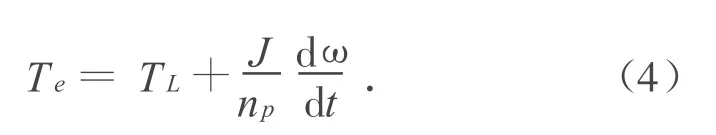
式中：Rs,Rr分别为定、转子电阻;Ls,Lr,Lm分别为定、转子自感及互感;ω1为同步角速度;ω为转子旋转角速度;np为电机极对数;TL为负载转矩;J为转动惯量;p为微分算子。

2 控制策略

选取d、q坐标系为同步旋转坐标系(m,t坐标系),采用定子磁场定向矢量控制,将m轴定于定子磁链矢量 Ψs方向上,对其速度和电流进行闭环控制,则双馈电机的数学模型变为[2,3]：

电压方程

磁链方程

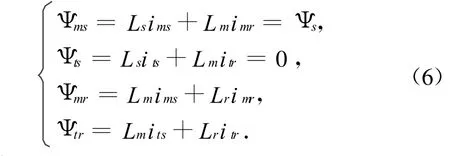
电磁转矩方程

由式(6)中的定子磁链方程整理得：

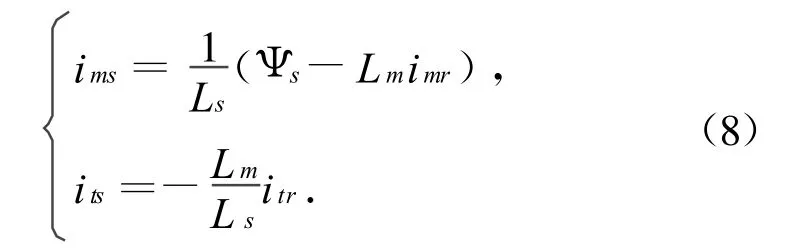
将式(8)代入式(3),整理得电磁转矩方程：

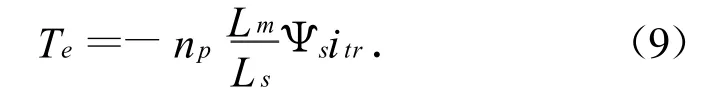
将式(9)代入式(4),整理得转速方程：

忽略定子电阻时,由式(5)可得系统稳态的定子电压和磁链方程为：

式中,us为定子相电压幅值。

因此得到双馈电机矢量控制系统原理见图1。

图1 双馈电机矢量控制系统

3 系统仿真模型

根据双馈电机矢量控制原理,在MATLAB6.5环境下搭建了仿真模型,转子侧IGBT的触发脉冲控制模块如图2所示,网侧IGBT的触发脉冲控制模块如图3所示。双馈电机参数如下：额定功率PN=2.2 k W;额定转速n N=1 420 r/min;定子额定电压UsN=380 V,f N=50 Hz;额定电流 IsN=5 A;转子额定电压Ur N=260 V,额定电流 IrN=6 A;极对数np=2;定子电阻Rs=3.2 Ω;转子等效电阻R′r=2.965 8Ω;定子漏感L s l=0.014 3 H;转子漏感 L r l=0.014 3 H;互感Lm=0.265 4 H 。

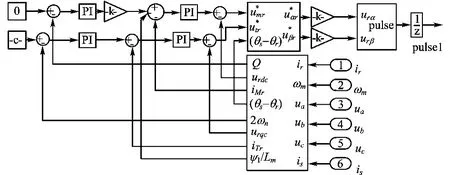
图2 转子侧IGBT脉冲触发仿真模型

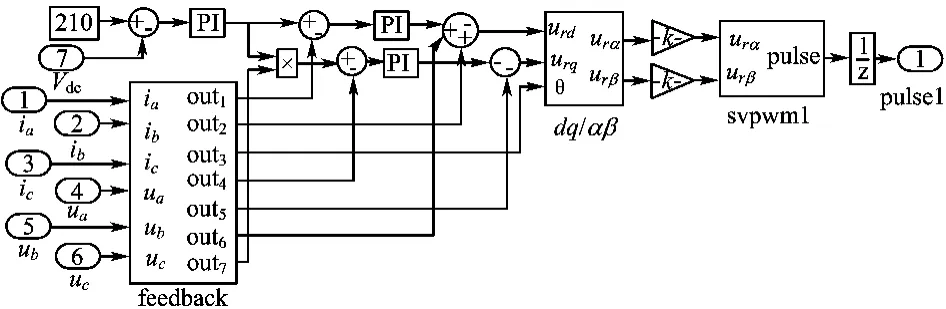
图3 网侧IGBT的脉冲触发仿真模块

4 仿真结果

次同步速,对电机进行调速。空载起动,0.2 s时加负载7.4 N◦m;速度给定0 s时1 337 r/min,2 s时1 241 r/min;仿真波形如图4所示。

图4 次同步速下调速的仿真波形

次同步速时,空载起动,0.2 s时加负载14.8 N◦m;转速给定为1 050 r/min,仿真波形如图5所示。

由次同步向超同步调速,空载起动,0.2 s时加负载14.8 N◦m;转速给定0 s时1 427 r/min,1.5 s时1 720 r/min,仿真波形如图6所示。

次同步速时,负载发生变化情况。速度给定为1 241 r/min,起动时负载转矩为4 N◦m,2 s时变为7.4 N◦m,仿真波形如图7所示。

图5 次同步速下的仿真波形

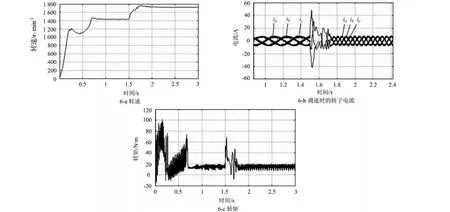
图6 由次同步速向超同步调速的仿真波形

从仿真结果可以看出：

1)给定速度变化后,速度和转矩可以快速的跟随变化,且超调量小。

2)系统的最高速可达到1 720 r/min,最低速达1 050 r/min,且稳态电流趋于正弦,谐波较少。

3)负载发生变化时,系统能够快速作出反应,定子电流变大,转子电流的频率随转速的变化而变化。因转速给定不变,所以转子电流的频率也不变。

4)电机由次同步向超同步调速时,转子电流的相序发生了变化,因此,转子侧的功率流向也发生了变化。转子侧的功率流向,由次同步时从电机流向电网,到超同步时功率从电网流向电机。

5 结论

通过对双馈电机在两相旋转坐标系下的模型分析,确定了以定子磁链定向的矢量控制策略,并依据该控制策略,搭建了双馈电机变频调速控制系统的仿真模型。通过分析其不同工况下的仿真结果可以看出,基本达到了预期的目的,验证了该调速系统的 有效性,可行性。

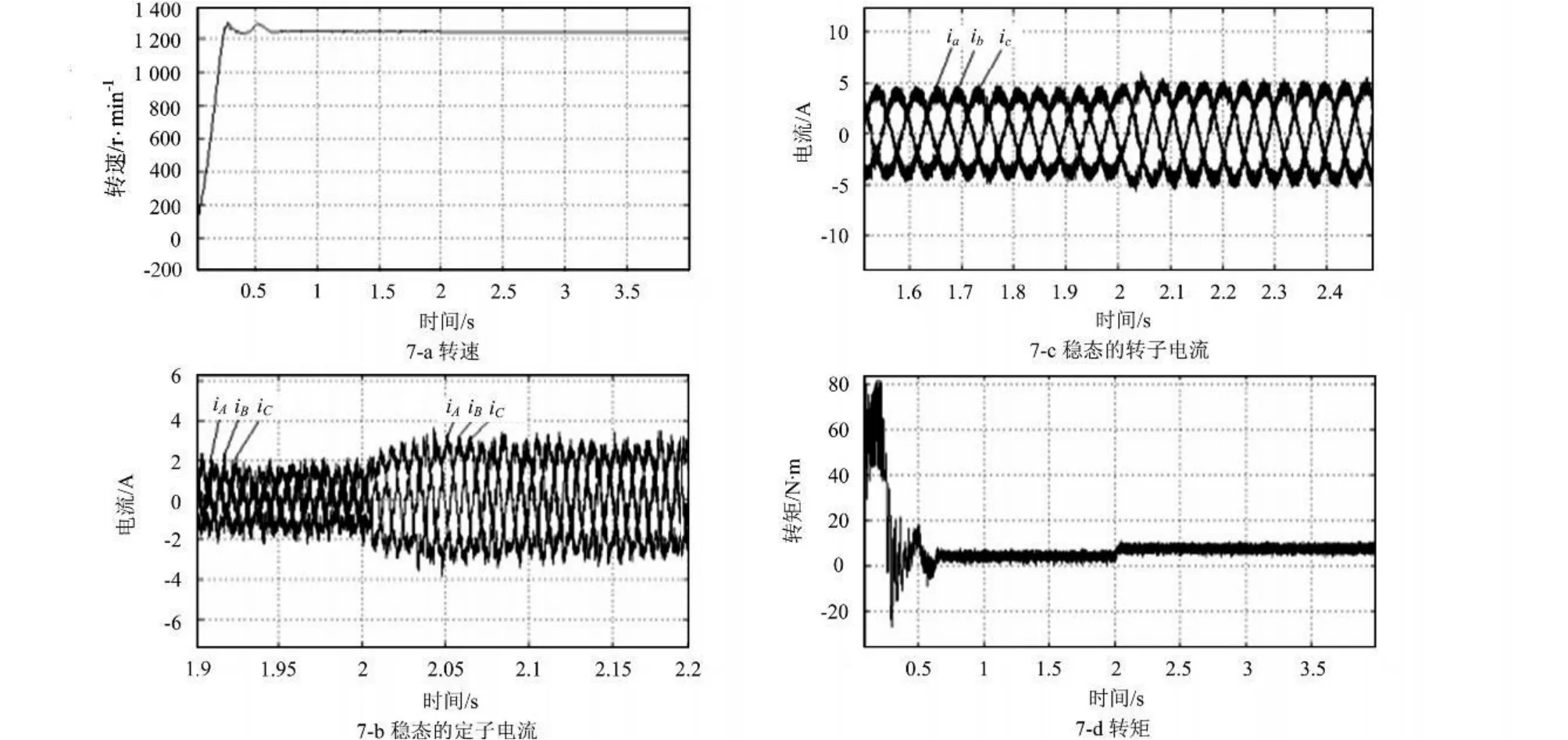
图7 次同步速下负载变化的仿真波形

[1] 陈伯时.电力拖动自动控制系统[M].北京：机械工业出版社,2003.

[2] 李娟娟.双馈电机矢量控制调速系统及仿真[D].合肥：合肥工业大学,2004.

[3] 洪乃刚.电力电子和电力拖动控制系统的MA TLAB仿真[M].北京：机械工业出版社,2006.