利用高程标准差表达地形起伏程度的数据分析

隋 刚,郝兵元,彭 林

(太原理工大学矿业工程学院,太原030024)

地形的起伏程度是表达某一区域地形特征的元素,一些资料中称之为“地形起伏度”。在土壤侵蚀、土地复垦、环境评价、采矿、地质、水利、交通等领域都涉及到相关内容,但是目前的地图学、地理学和测绘学科均没有“地形起伏度”的确切定义,国际地理联合会地貌调查与制图委员会建议用指定区域内最大高程与最小高程的差值来表达地形的起伏程度,也就是高程差法,并在其编制的欧洲1∶250万地貌图中,规定地势起伏度的统计单元面积为16 km2。依据高程差法,涂汉明、刘振东结合中国地貌类型的基本特征,论证了中国地势起伏度最佳统计单元的存在,得出我国地势起伏度最佳统计单元为21 km2[1,2];刘新华基于我国1∶100万DEM,经过统计、分析得出基于该数据的我国地形起伏度最佳统计窗口大小为5 km×5 km[3]。刘爱利、汤国安基于1：100万 DEM 数据统计分析后,认为6.5 km×6.5 km为我国地形起伏度最佳统计窗口[4]。程维明分析得出1∶10万、1∶25万、1∶50万、1∶100万、1∶400万比例尺数据分别对应0.4,4,12,18,21 km2为我国地形起伏度最佳统计窗口[5,6]。

1 高程差表达地形起伏程度的问题

用最大高程与最小高程的差值表达地形起伏程度的方法存在的问题是,不同比例尺数据,同一区域的最佳统计窗口差别很大。反映出这种方法的不稳地性。同时,这一方法不能反映地貌的局部起伏变化状况。如图1所示,4个最大、最小高程差相同的地形,但地貌却明显不同,如果用这种方法就认为四者有相同的起伏度。还有,最佳统计窗口一般都是用回归方法统计计算出来,而且不同地区的数据收敛窗口面积不同,数据实验证明窗口面积一般要接近5 km×5 km左右,统计结果才会收敛[7-11]。这样大面积的统计窗口,对于全国的宏观地貌分类具有指导意义,但对于地区、县、乡级应用基本没有实际意义,所以应该积极探索其它的方法来表达地形的起伏程度。

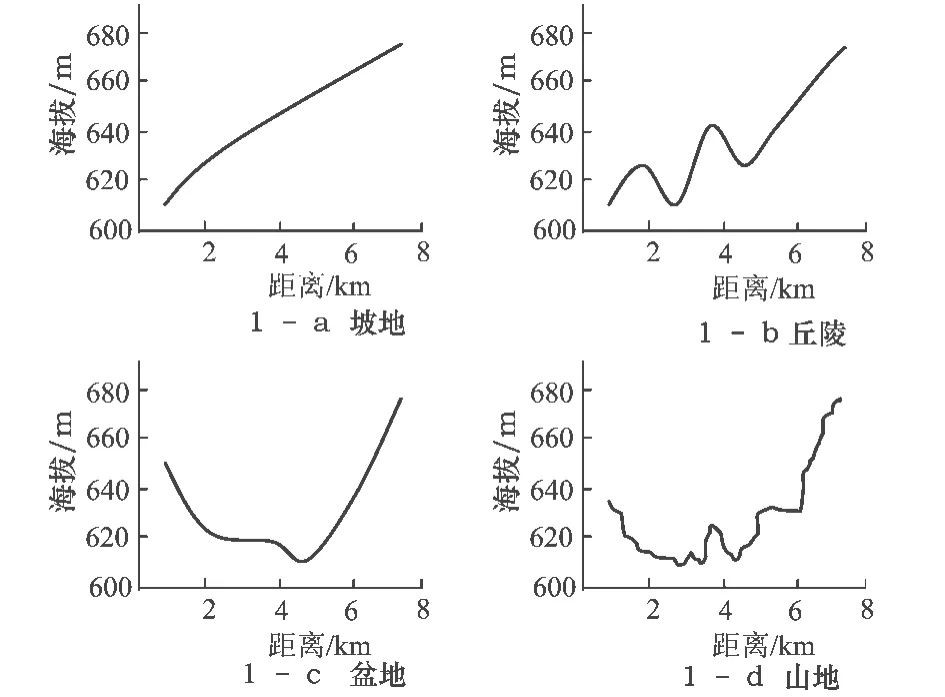
图1 最大高程与最小高程的差值相同,地貌不同的地形剖面图

2 高程标准差表达地形起伏程度原理

标准差也称均方差,一般用σ表示,具体的数学定义如下。

设有一组数值x1,x2,…,x N(均为实数),其平均值为：

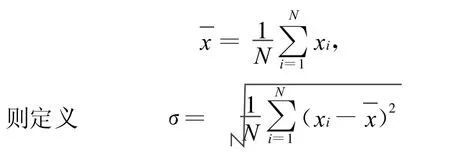
为这一组数值的标准差。

根据定义,标准差是一种平均数,它反应了一组数值中某一数值与其平均值的差异程度,经常被用来评估一组数值变化或波动程度。在测量学中,经常用标准差衡量误差分布的离散程度。因此,如果将xi换成某一区域的高程值,则标准差就成为“高程标准差”。高程标准差的值越大,高程波动的范围就越大,地形也就越不平坦,这样就可以用高程标准差来衡量地形的起伏程度。

实际工作中,可以选择矩形窗口或者圆形窗口来计算这一区域内的高程标准差,让这个窗口在某一数据区内以一定的步长和方向移动,这样就可以计算出整个数据区的高程标准差分布图,从而表达地形的起伏状况。由于高程标准差计算用到了这一区域内所有点的高程值,而最大高程值和最小高程值之差的方法,仅仅用到两个点的高程值,因此标准差方法更能综合反映这一区域的地形起伏状况,而且能够反映出地形的局部起伏变化。

实际上,标准差方法已经在许多行业被用来衡量数据的变化状况,但由于数据计算量比较大,同时缺少相应的支持工具,所以应用高程标准差表达地形起伏程度的应用还没有见到。近年来GIS技术的快速发展,为我们提供了方便快捷的分析计算工具,使得用高程标准差方法计算地形起伏程度成为可能。

3 数据计算与分析

以朔州市1∶10万和阳曲县1∶5万DEM 为实验数据进行了数据计算和分析。朔州境内地形地貌复杂多样,平原、丘陵、山川都有典型分布。东部为平原,北部为典型高原地貌,丘陵起伏,沟壑纵横,如图2所示。首先利用ArcMap软件,将1∶10万DEM数据转换成分辨率为20 m×20 m的栅格数据,按高程值进行分级统计,如图3所示,可以看出朔州市的最高海拔和最低海拔之差有1 300 m以上,地势起伏比较大。

然后应用ArcMap中的Neighborhood Statistics计算工具,选择100 m×100 m,200 m×200 m,300 m×300 m,…,3 000 m×3 000 m为统计窗口,分别计算高程标准差,计算结果采用等间隔分级,典型的计算结果如图4～图9所示。

图2 朔州市DEM与landset 7遥感影像叠加图

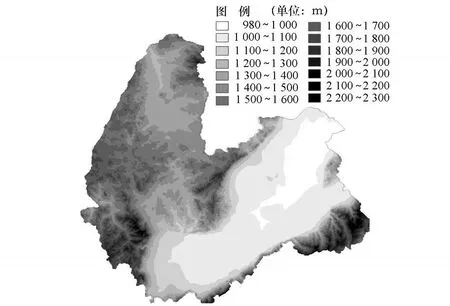
图3 朔州市高程分布图

通过数据分析可以发现,当统计窗口面积小于600 m×600 m时,高程标准差的值比较小,分级不明显;当窗口面积大于1 500 m×1 500 m时,高程标准差的值越来越大,分级变得模糊,地貌类型的区分不明显;当窗口面积在800 m×800 m到1 200 m×1 200 m时,尤其为1 000 m×1 000 m左右时,高程标准差的值分布比较合理,对地形地貌分的比较清楚,并且分级的边界与遥感影像解译的地物分类比较吻合,如图2,图7,图10所示。经过多次实验发现,在 ArcMap中选择 Natural Breaks(自然间隔)分类方法,将高程标准差非均匀分为5类时,即0～10,10～30,30～50,50～70和＞70,地形起伏的分类比较明显,如图11所示。高程标准差在0～10之间的地形非常平坦,基本都是耕地,10～30为相对平坦的草地,30～50之间的一般为起伏的丘陵,大于50的基本都是沟壑纵横的山区。

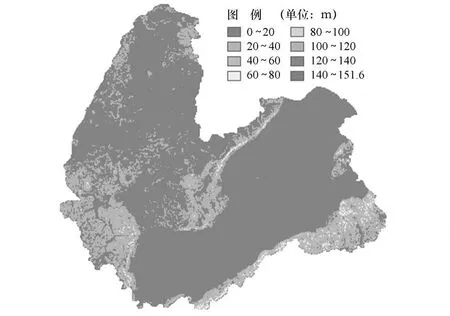
图5 600 m×600 m窗口高程标准差分布图

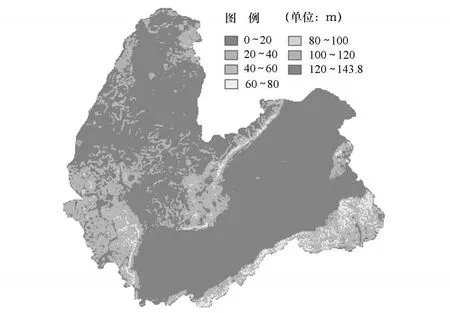
图6 800 m×800 m窗口高程标准差分布图

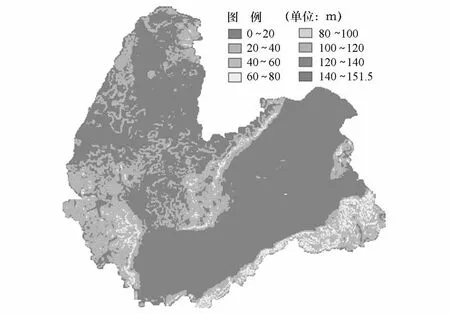
图7 1 000 m×1 000 m窗口高程标准差分布图

应用相同的方法和过程,对阳曲县1∶5万DEM数据进行了数据计算和分析,得出了与朔州市1∶10万DEM数据计算非常一致的结果,如图12和图13所示。朔州市面积为10 600 km2,阳曲县面积为2 070 km2,朔州市用的是1∶10万DEM 数据,阳曲县用的是1∶5万DEM 数据,但应用相同的统计窗口和分级标准,分类结果基本相同。这说明高程标准差分级方法的适用性和稳定性都比高程差方法好。

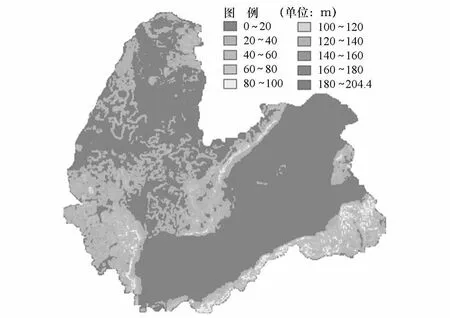
图8 1 200 m×1 200 m窗口高程标准差分布图

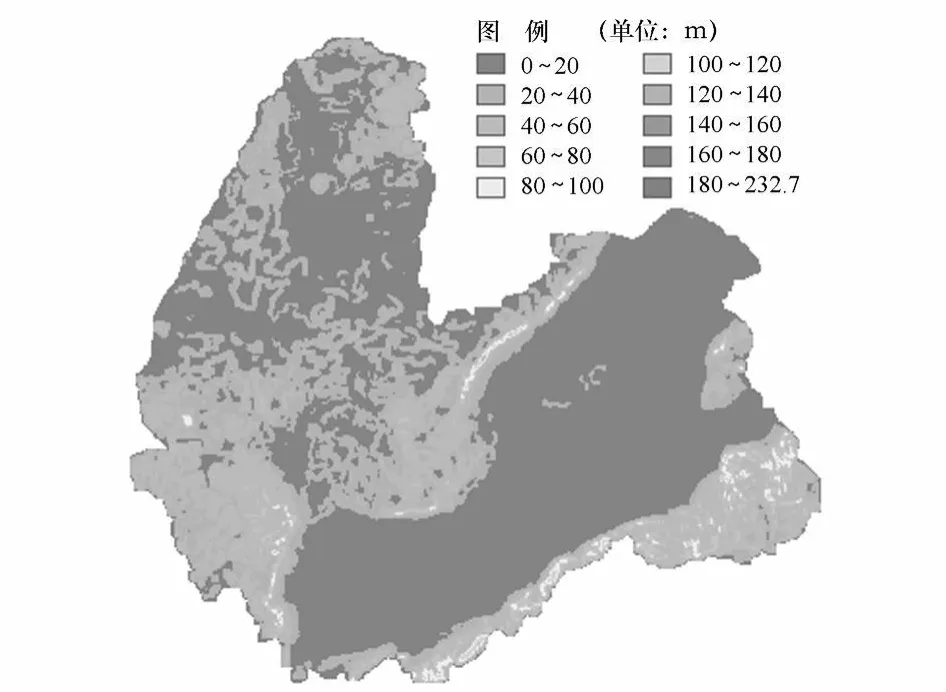
图9 1 500 m×1 500 m窗口高程标准差分布图

图10 朔州市土地利用现状图

4 结论与探讨

1)高程标准差能够清晰的表达地形的起伏程度,对地形的局部变化也能较灵敏地反映出来,其适用性和稳定性都优于高程差方法。

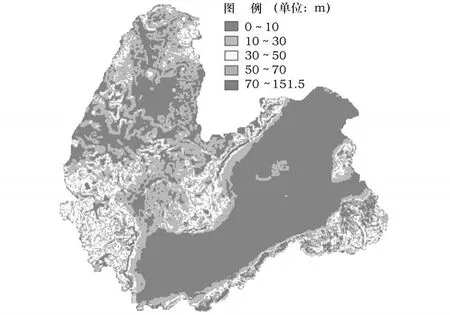
图11 1 km×1 km窗口高程标准差不均匀分级图

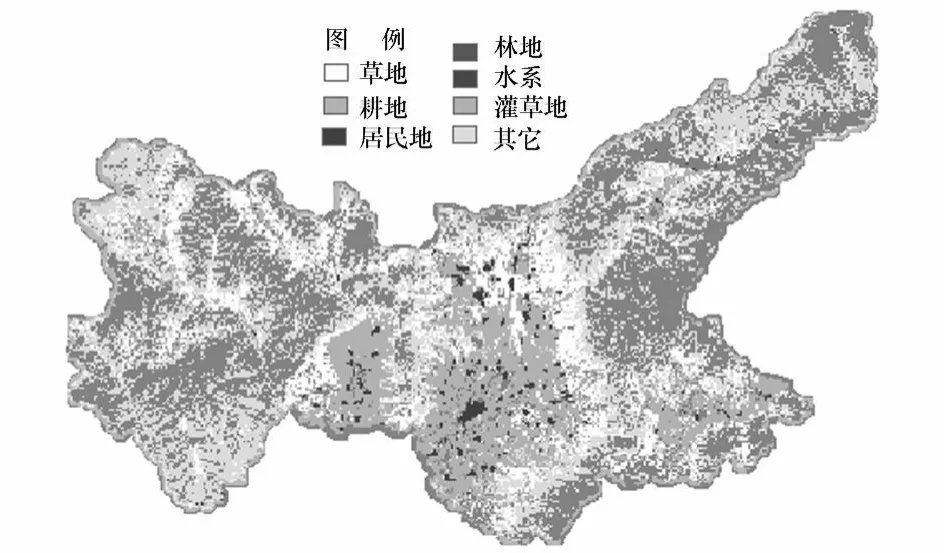
图12 阳曲县土地利用现状图

2)分析结果与栅格单元的大小、分析窗口大小的选择有关。合理选择分析窗口面积,高程标准差能够较好的描述地形的起伏程度,选择1 000 m×1 000 m左右的矩形分析窗口,平川盆地、半坡丘陵、山区能够很好的分级。当采用“自然间隔分类”方法时,地貌的分类效果更好。

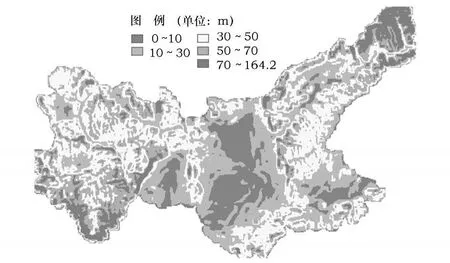
图13 1 km×1 km窗口高程标准差不均匀分级图

3)只要窗口面积相同,在地形中没有平行窗口边界的陡峭地形的情况下,选择圆形窗口或矩形窗口做计算,对结果的影响不大。

由于没有用高程标准差方法表达地形起伏度的参考案例,计算结果也是在特定地区的地形数据上计算得出的,因而结论可能具有局限性。窗口的大小、栅格单元的大小、标准差的分级等都有待于通过更多的实验数据来验证,以便发现规律,制定标准,促进应用。同时,这种方法也存在计算量大的缺点,当统计窗口面积为2 000 m×2 000 m时,朔州市的地图,双核CUP,2GB内存的计算机用了近11 h才算出结果,更大的窗口会用1 d甚至更长的时间才能计算出结果,所以应用不太方便。

[1] 涂汉明 刘振东.中国地势起伏度最佳统计单元的求证[J].湖北大学学报(自然科学版),1990,12(3)：266-271.

[2] 涂汉明,刘振东.中国地势起伏度研究[J].测绘学报,1991,20(4)：311-319.

[3] 刘新华.区域水土流失地形因子分析与提取研究[D].杨凌：西北农林科技大学,2001.

[4] 刘爱利.基于1∶100万DEM的我国地形地貌特征研究[D].西安：西北大学,2004.

[5] 程维明,周成虎,柴慧霞,等.中国陆地地貌基本形态类型定量提取与分析[J].地球信息科学学报,2009,11(16)：725-736.

[6] 郎玲玲,程维明,朱启疆,等.多尺度DEM提取地势起伏度的对比分析——以福建低山丘陵区为例[J].地球信息科学,2007,9(6)：1-7.

[7] 闾国年,钱亚东,陈钟明.基于栅格数字高程模型提取特征地貌技术研究[J].地理学报,1998,53(6)：562-569.

[8] 周侗,龙毅,汤国安,等.面向DEM 地形复杂度分析的分形方法研究[J].地理与地理信息科学,2006,22(1)：26-30.

[9] 朱红春,陈楠,刘海英,等.自1∶10000比例尺DEM 提取地形起伏度——以陕北黄土高原的实验为例[J].测绘科学,2005,30(4)：86-89.

[10] 汤国安,宋佳.基于坡度图制图中坡度分级方法的比较研究[J].水土保持学报,2006,20(2)：157-192.

[11] LI Ben-gang,TAO Shu.Several problems and their solutionsin surface runoff modeling[J].Bulletin of Soil and Water Conservation,2000,20(3)：47-49.