紊流中泥沙颗粒的跟随性分析

2010-09-13王鸿翔

太原理工大学学报 2010年4期

张羽,王鸿翔

(华北水利水电学院,郑州 450011)

1 异质粒子与紊流的跟随性

与流体质点不同容重的粒子,如泥沙或其它污染物等,称之为异质粒子。异质粒子受紊流场的作用,反之又影响紊流场。由于流体中含有粒子以后要引起附加紊动耗损,此能量耗损是由于粒子和流体质点之间紊动运动的滞后作用所引起的,而且随着波数的增加迟后作用增加。有理由认为,紊流场中异质粒子的出现,主要影响高波数层中的紊动能谱。因此,需要研究粒子在紊流场中的跟随性问题。

紊流力学认为[1],异质粒子跟随流体运动的程度,取决于粒子的粒径d p、粒子的密度 ρp、流体的粘性系数μ、流体的密度ρ、紊流的紊动强度及脉动频率f等,若以粒子的速度vp和流体的速度v的比值v p/v表示异质粒子跟随流体的程度,则其函数关系为：

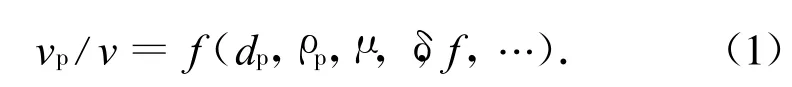
若v p/v=1,表示粒子完全跟随流体;v p/v＜1表示粒子滞后。如果能建立上式的具体表达形式,即可预测泥沙及模型沙的跟随程度。

首先将紊流流速v用Fourier积分表示,即

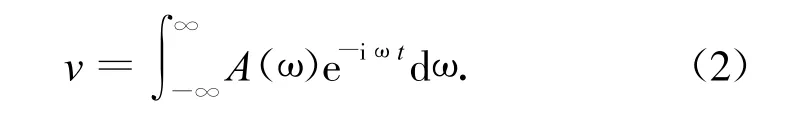
粒子在紊流带动下的运动,并不完全跟随流体,表现为粒子速度vp的幅值和相角与流体的速度v不同,因此,对应于式(2),粒子速度v p可表示为：

式中：A(ω)为振幅;η(ω)为粒子速度与流体速度幅值之比;φ(ω)为粒子速度与流体速度相角之差。当η=1,φ=0,表示粒子完全跟随流体一起运动,如果粒子滞后于流体,则η＜1,φ＞0。

为了具体地计算η和ω,按照一般教科书的做法,可以利用Basset-Boussinesq-Oseen方程(简称BBO方程)来实现。BBO方程是描述紊流场中单个粒子的运动方程,其具体形式为：

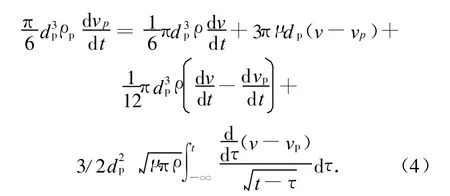
式中：左边项代表粒子的惯性力;右边第一项为流体加速引起的压力梯度作用于粒子的力;右边第二项为黏性阻力;右边第三项为粒子加速运动的附加质量力;右边第四项为Basset力,它是计算流体图型偏离定常状态时的附加力,当粒子用高速率加速时,它成为重要的量,所产生的阻力比定常状态的大许多倍。

将上式改写成：

式中：

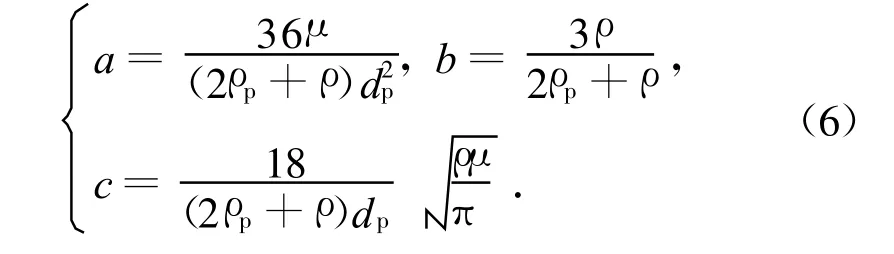
用式(2)和(3)计算式(5)中各项,得

由式(7)得到最后的结果为：

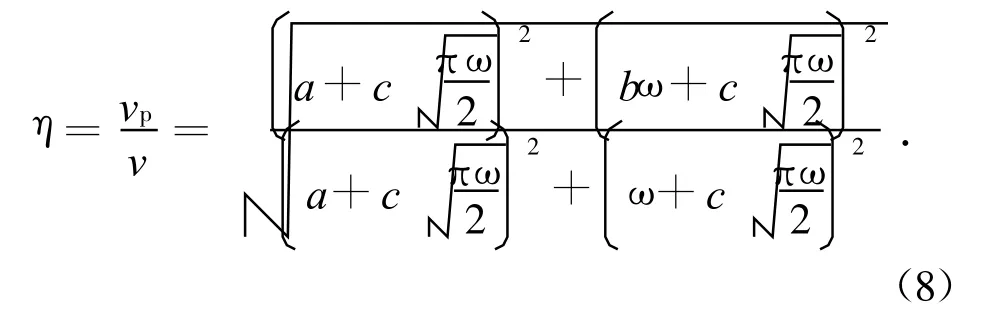
式中,ω为圆频率,即 ω=2πf,f为频率。

2 计算与讨论

根据天然河道及模型水流常见紊动频率范围 f(10～300 Hz),对于不同粒径的天然沙,其跟随度与紊流频率的关系见图1。表明粒径大于0.1 mm的天然沙的跟随性很差,因而难以呈悬移质运动状态,只有粒径小于0.1 mm的颗粒,才有较大的跟随度,从而在水流中处于悬浮状态,这种计算在定性上是符合天然实际的。此外,从该图中也可看出,只有小于0.05 mm之后的细沙跟随度才逐渐增加,在紊流中才容易处于悬移状态,正因为如此,众多天然河流中的悬移质往往以0.015～0.03 mm的泥沙为主体。至于粒径为0.01 mm的泥沙,因在不同的紊流频率下都有较高的跟随度,从而在自然河流中这种细颗粒必然成为“穿堂而过”的冲泻质[2]。

图1 天然沙不同粒径跟随度与频率的关系

进一步计算容重小于天然沙的模型沙在紊流中的跟随度,其结果见图2—图5。表明在常见频率范围内,随着模型沙容重的逐渐减小,相同粒径的模型沙跟随水流质点的运动逐渐增强。这也可以说明运用塑料沙做为模型沙时,由于塑料沙与水流的跟随性较强,即使在试验中模型加沙量很多,水流亦能够挟带而下,但参与河床交换的颗粒仅少量部分。此种情况下模型水流的挟沙能力大于原型,亦即远比原型河道水流强度为弱的模型河道需要挟带更多的模型沙,才能满足河床冲淤变形相似。显然如此模拟河道河床冲淤变形相似,存在严重的失真现象。

图2 电厂煤灰不同粒径跟随度与频率的关系

图3 拟焦沙不同粒径跟随度与频率的关系

图4 电木粉不同粒径跟随度与频率的关系

图5 塑料沙不同粒径跟随度与频率的关系

由图2—图5可看出,容重偏大的电厂煤灰和容重适中的拟焦沙作为模型悬沙时(如粒径为0.025 mm),图中曲线与天然沙在定性上较为接近;容重偏小的电木粉在粒径较大时即表现出较大的跟随度,与天然沙粒径较小时的跟随度相当;尤其是容重过小的塑料沙作为模型沙时,在粒径为0.25 mm时,图中曲线表明仍会出现悬浮状态。由此表明,采用轻质沙作为模型沙时,容易使粒径出现严重的变态,且因有很高的跟随度而使模型在进口加沙量很大时仍难落淤,从而表现出较大的水流挟沙能力,这似可说明轻质沙作为模型沙时,其含沙量比尺就有可能出现小于1的失真现象。

从实际的悬移质动床模型实例也可发现,模型沙容重很小时,因与水流的跟随性过强,即使在含沙量比尺小于1、泥沙粒径偏粗的条件下,也不会出现河床淤积偏多的变形情况,从而时间变态所引起的问题也有可能得到一定程度的弱化。

综上所述,在常见频率范围内,随着模型沙容重的逐渐减小,相同粒径的模型沙跟随水流质点的运动逐渐增强。这也可以说明运用塑料沙做为模型沙时,由于塑料沙与水流的跟随性较强,即使在试验中模型加沙量很多,水流亦能够挟带而下,这样模型水流的挟沙能力大于原型,亦即远较原型水流强度为弱的模型小河就有可能挟带更多的模型沙。