可变阶次的分抗元件的电路实现

张 松

（成都电子机械高等专科学校通信系，四川 成都 610031）

0 引言

分数阶微积分运算是整数阶微积分运算概念的延伸，分数阶运算包括分数阶导数和分数阶积分、分数阶傅里叶变换等，它们是分析和处理许多“非”问题和现象(比如非线性、非因果、非最小相位、非高斯、非平稳、分数布朗运动、混沌等)的有用工具[1]。该问题曾被许多大数学家，如Leibniz、Euler、Liouville等研究过，但是把微积分的阶次推广到分数甚至复数领域，因其计算复杂，过去只是数学家研究的对象。随着信息科学的迅猛发展,分数微积分的应用也已逐渐渗透到许多工程应用领域, 如各种材资的记忆、力学和电特性描述、粘弹性阻尼器、分形理论等。分数阶运算在很多问题的处理过程中所拥有的整数阶运算无可比拟的优点正逐渐显露出来[2]。

数学家们从各自不同的角度入手，给出了分数阶微积分不同的定义，如GL(Gainwald—Letnikov)定义、RL(Riernarm—Liouville)定义、Caputo定义等。

从信号处理角度出发，考虑分数演算的频率域定义为[3]：对于可微的信号f(t)，其傅立叶变换为，即其中v为分数演算的阶数（0＜v＜1），可得到分数演算算子在频域的指数形式为

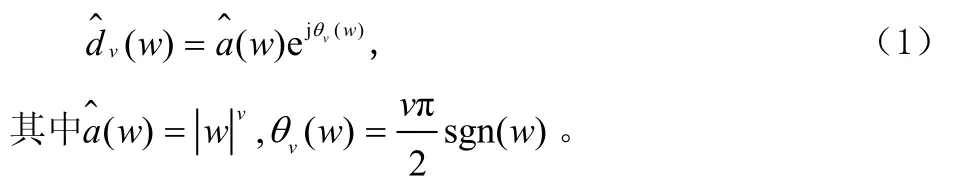
将该定义应用到拉普拉斯变换，即 f( t) ↔ F( S),则将 Sv定义为拉氏分数演算算子。

拉氏分数演算算子的电路实现将为分数阶微积分的工程应用铺平道路。一些研究者提出了一些实现方法，但这些方法都存在着不同的缺陷。例如：阶数限制于1/2阶，其它阶数不易实现[4]。分抗元件由局部和整体具有高度自相似的分形电路实现，电路元件为无穷多个，不利于集成化。

为此,在参考文献[5]的基础上，设计了一款任意阶分抗元件，给出其具体设计步骤，并利用该分抗元件可获得信号的任意分数阶微分或积分信号，通过仿真验证了本设计的正确性。

1 分数阶函数（Sν）的逼近

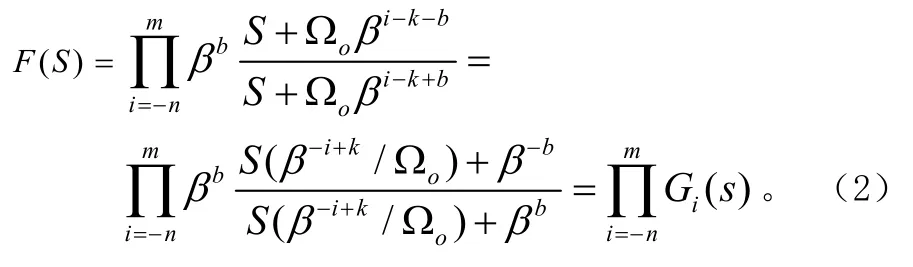
定义每一级双线性级联函数如式（3）所示，将其定义为分数阶函数的基本模块函数。

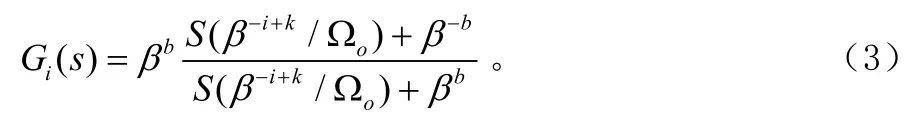
假设待实现的分抗阶数为ν=1/3，待逼近的频率段为（ ΩL,ΩH），其中 ΩL= 2πrad/s,ΩH= 2π ⋅ 106rad/s ，在该频率段内允许的最大逼近误差为 εmax= 0 .3 d B ，那么如何实现呢？

⑤令 Ci= β-i+k/Ωo，可得 Ci如下：

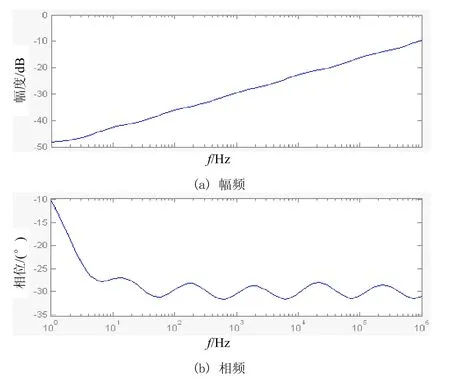
图1 1/3阶分抗元件的幅频和相频特性

2 可变阶次分抗元件的电路实现

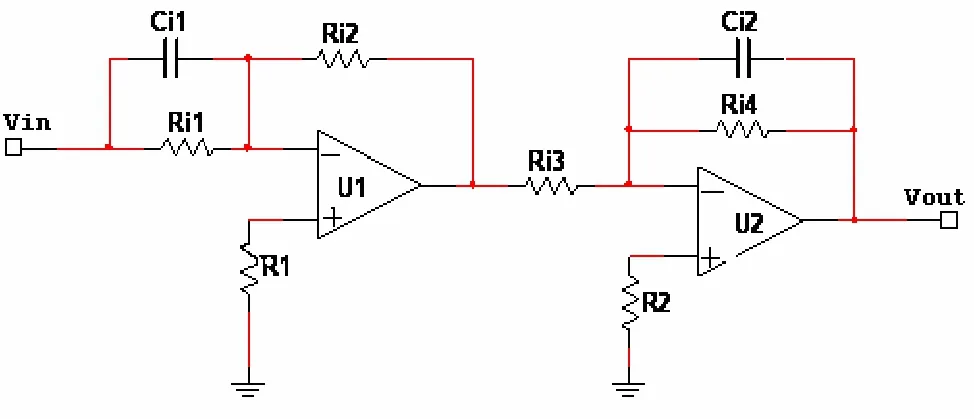
图2 由比例微分环节和惯性环节组成的基本模块函数

由比例微分环节和惯性环节的传递函数特性，可得电阻、电容参数的设计如式（4）所示：

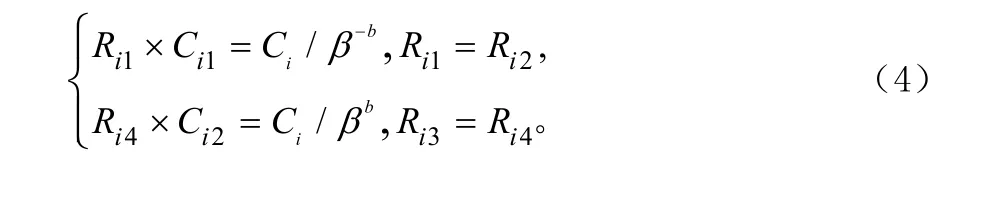
3 电路仿真结果

根据式（2）和式（4）得到其1/3阶分抗元件，将如图2所示的7级电路级联，其电路如图3所示[8]。

按照式（4）计算相应的电容电阻值，此处选择电容在nF或pF范围内，电阻为1 kΩ到1 MΩ之间，运放选用NE5532，通过Pspice仿真，得到其对应的幅频和相频特性如图4所示。将图4和图1比较可知，其电路仿真结果和理论值基本符合。

图3 1/3阶分抗元件电路

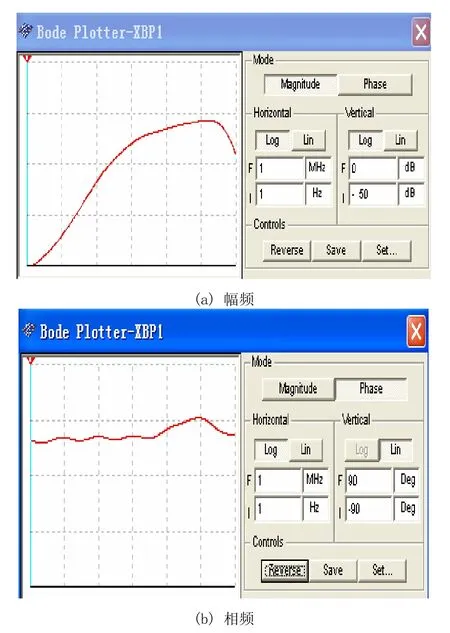
图4 1/3阶分抗元件的幅频和相频特性

4 结语

近年来,分数阶微积理论成为人们关注的重要课题，如何将分数阶运算从理论走向各应用领域，分抗元件的实现是非常重要的环节。利用线性电路完成了可变阶次的分抗元件的设计，其设计和实际制作结果逼近理论值，设计电路简单，容易集成，可根据工程应用需要生产不同类型的分数阶芯片，对工程设计具有指导意义。

[1] 袁晓,张红雨,虞厥邦.分数导数与数字微分器设计[J].电子学报,2004(32)：1658-166.

[2] OLDHAM K B, SPANIER J. The Fractional Calculus[M]. New York and London： Academic Press,1974.

[3] 袁晓,陈向东,李齐良,等.微分算子与子波构造[J].电子学报,2002(30)：769-773.

[4] 廖科,袁晓,蒲亦非,等. 1/2阶分数演算的模拟OTA电路实现[J].四川大学学报：工程科学版,2005(37)：150-154.

[5] HISANO T.A Realization of SαTransfer Function[J].Proc.IEICE Fall Conf’.,1992(A-26)：92．

[6] [美] 奥本海姆 A Y,谢弗 R W,巴克 J R.离散时间信号处理[M]．第2版.刘树棠，黄建国,译．西安：西安交通大学出版社，2005：171-180.

[7] [美]赛尔吉欧.佛朗哥.基于运算放大器和模拟集成电路的电路设计[M]．第3版.刘树棠，朱茂林，荣玫,译．西安：西安交通大学出版社，2004：310-345.

[8] 熊伟,侯传教,梁青,等．Multisim7电路设计及仿真应用[M].北京：清华大学出版社，2005：247-251.