超混沌LC振荡电路的混合反馈同步与保密通信

户永清

（四川文理学院，四川 达州 635000）

0 引言

自从Pecora和Carroll提出利用混沌同步进行保密通信和信息处理的实验方案后，相继出现了多种基于同步混沌实现保密通信的方法。由于混沌系统对初值的极端敏感性、内随机性、类噪声性、宽带功率谱和快速衰减的相关函数，使得其特别适合于采用宽谱发射来实现保密通信。但是，目前大部分混沌同步方案还只是停留在具有一个正的 Lyapunov指数的弱混沌系统上，而具有两个及其以上正的 Lyapunov指数的超混沌系统，由于其至少在一个环面上产生收缩和发散，因而相对于一般的混沌系统有着更为复杂的动力学行为[1]。因此，利用超混沌系统的同步来进行通信比一般的混沌通信具有更好的保密性、更大的存储容量、信息处理能力和更强的鲁棒性[2]。基于上述原因，现在超混沌电感电容振荡电路的基础上提出了一种线性和非线性混合反馈同步方案，通过设计李雅普诺夫函数对系统同步的稳定性进行了分析，得出了稳定状态下系统反馈强度的临界值。同时，针对一般的混沌同步通信只能传输能量极小的信号、有用信号浮在混沌载体上而不是融入到混沌载体中[3]、信号极易被破译等一系列问题，通过利用上述同步方案将有用的信息信号注入到混沌信号中，使有用信号和混沌载波信号融合在一起，既增强了通信的保密性，同时也提高了传输信号的能量和通信系统的效率。

1 超混沌LC振荡电路的混合反馈同步

简单的超混沌LC振荡电路模型是由A.Tamasevicius等人[4]提出的，它由运算放大器构成负阻元件。其无量纲动力学方程描述如下：

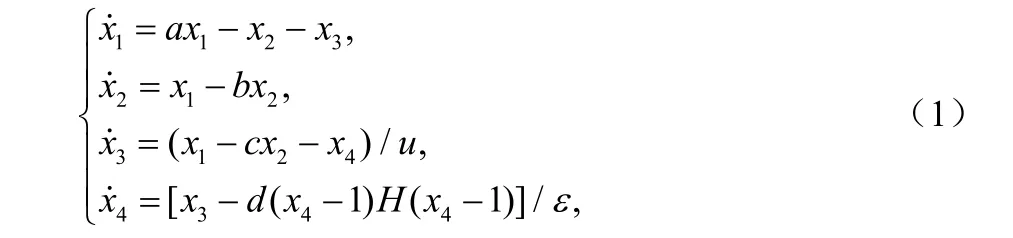
式中为a、b、c、d、u和ε为系统参数，H(·)为阶跃函数。经文献[4]研究,当系统参数为： a=0.6，b=0.05，c=0.015，d=10，u=0.3，ε=0.33时，超混沌LC振荡系统（1）有两个正的 Lyapunov指数：λ1=0.11，λ2=0.06，此时系统处于超混沌运动状态。

在式（1）的基础上，通过运用线性和非线性混合反馈控制的方法，构造如下的响应系统：

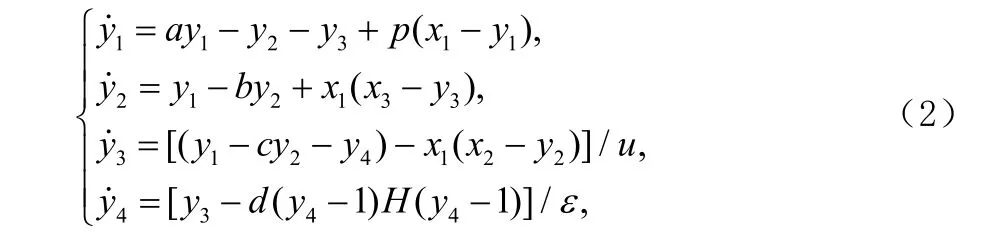
令轨道误差满足：

则误差动力学系统为：

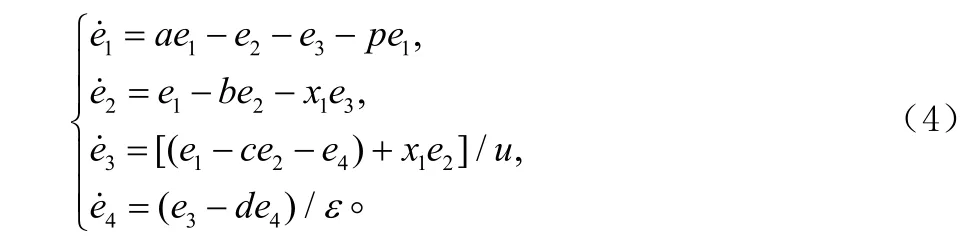
于是，超混沌LC振荡电路的同步问题就等价于误差系统（4）在零点的稳定性问题。构造如下Lyapunov函数：

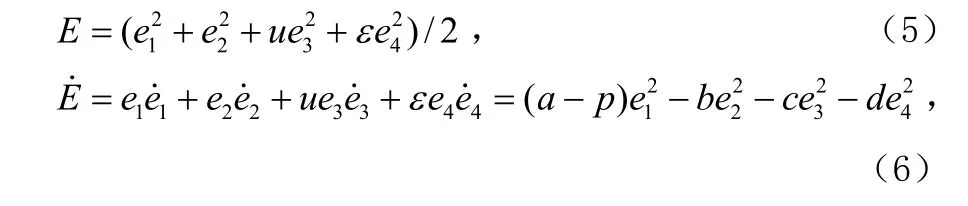
式（6）中b，c，d均大于0，若要式（6）为负值，则只需a ＜ p 即可。当 a ＜ p 时，有 E˙＜ 0，根据 Lyapunov 稳定性定理可知式（4）零解渐近稳定。即当 t→∞时，Y→X，响应系统（2）和驱动系统（1）达到同步。

为了验证上述理论分析的正确性，通过运用四阶龙格一库塔法进行数值模拟。其中驱动系统（1）的初值取为（0.5,0.2,0.1,0.3），响应系统（2）的初值取为（10.1,8.2,15.3,12.4）,p =10.0，积分步长为0.001（以下均同），定义为同步误差。数值模拟结果如图1和图2所示。图1为同步过程中的误差曲线，图2为同步后状态变量x1-y1的相图。可见，只需很短的时间同步误差就收敛为零，两系统就可以实现精确同步。

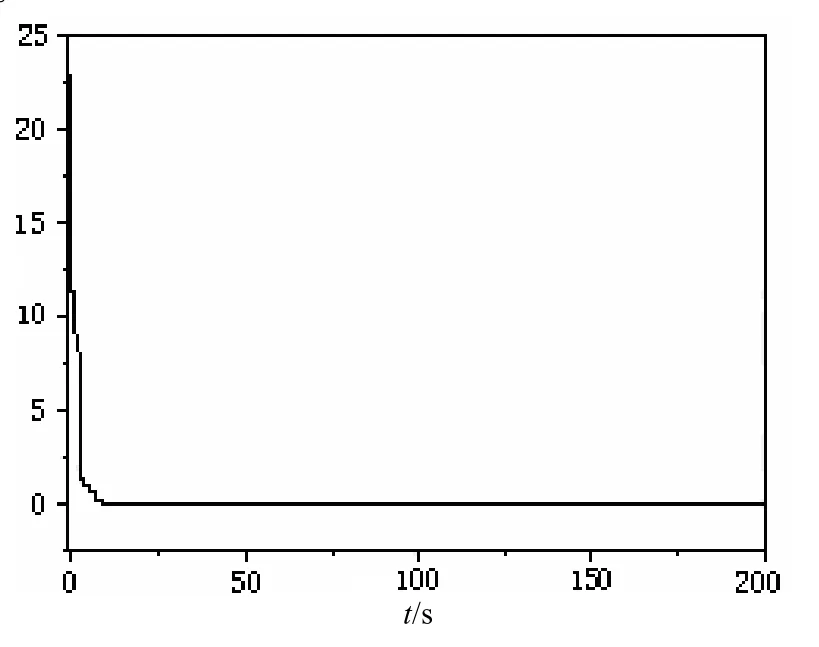
图1 同步过程中的误差曲线

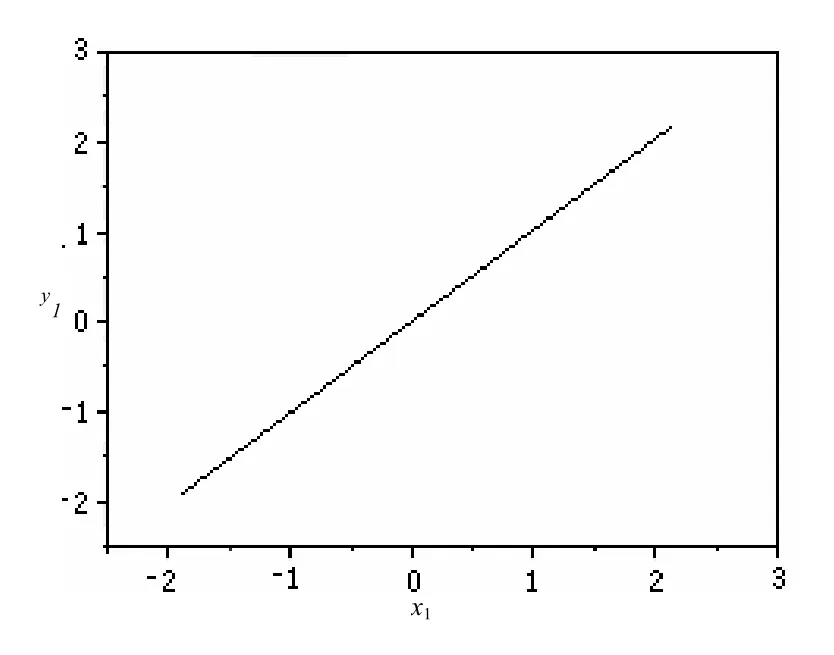
图2 同步后状态变量x1-y1的相图

2 超混沌电路注入式保密通信

对于一般的混沌掩盖保密通信，有用信号只是叠加在从发射系统发射出来的混沌信号上，即浮在混沌载体上，而不是融入到产生混沌的系统中，从而保密性能差，信号极易被破译。而且所携带的信号强度不能很大，否则发送系统和接收系统根本无法获得同步，这就导致通信系统的信噪比低，传输信号容易受信道噪声的干扰，稍大的噪声就会使接收端的信噪比减小，因而很难适应于工程应用。利用超混沌系统的同步，通过将信号直接注入到发射系统来进行保密通信，这样信息信号就融入到混沌载波信号中，有效地解决了上述问题。

具体方法描述如下：

考虑给定的n维混沌动力学系统

采用注入式保密通信方案时，设计发射端混沌系统、发射信号、接收端混沌系统和解调信号分别为：发射系统：

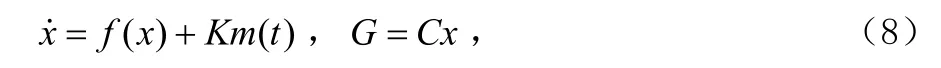
发射信号：

接收系统：

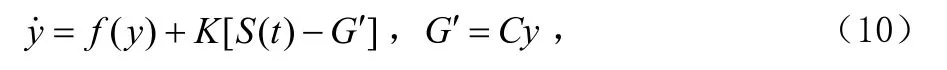
解调信号：

式中，m( t)为信息信号，S( t)为传输信号，m′( t)为解调信号， K ∈ Rn×1为反馈矢量，G∈R为发射系统输出信号，G′∈R为接收系统输出信号，C ∈ R1×n为输出矢量系数矩阵。

对于四阶超混沌LC振荡电路，选取C =（1,0,0,0），K =(k,0,0,0)T。采用基于混合反馈的混沌同步注入式保密通信方案时，相应的发射系统、发射信号、接收系统和解调信号分别如下式（12）、式（13）、式（14）、式（15）示：

发射系统：

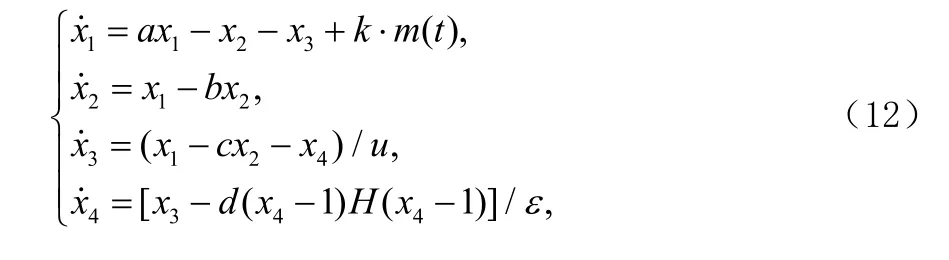
发射信号：

接收系统：

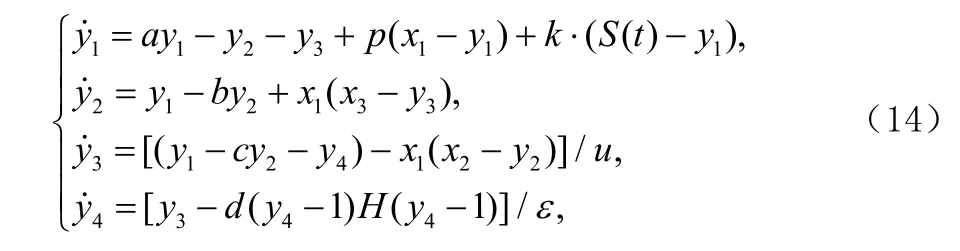
解调信号：

由条件 Lyapunov指数稳定性判据可知：当响应系统的所有条件 Lyapunov指数都为负值时，响应系统与驱动系统达到同步，这是保密通信方案设计的前提。为了确定响应系统的李雅谱诺夫指数为负时反馈强度的取值范围，利用四阶龙格一库塔法对上述过程进行模拟仿真。假设信息信号图3(a)、图3(b)分别给出了A =10.0和A =100.0时反馈强度k与响应系统的李雅谱诺夫指数的关系曲线。由图 3(a)、图 3(b)可知：在保证信息信号无失真恢复的条件下，信息信号能量较小时(如A=10.0)，k的取值范围较宽；能量较大时(如 A =100.0 )，k的取值范围较窄，例如当 k＞18.1时，响应系统的李雅谱诺夫指数为正，此时两系统将无法达到同步。

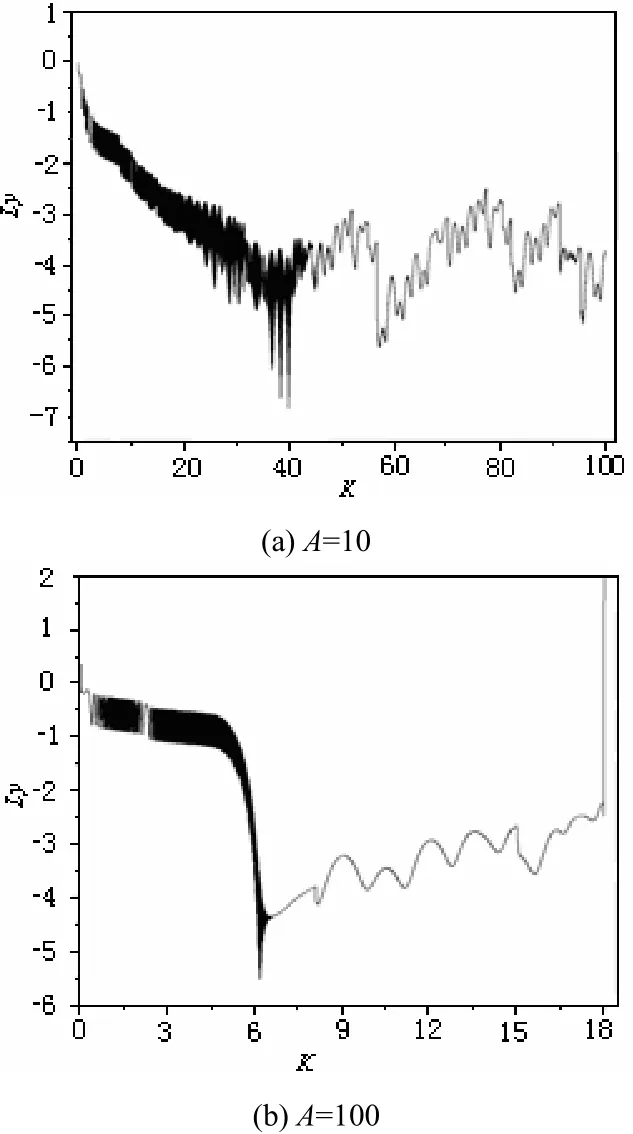
图3 响应系统的李雅谱诺夫指数和k的关系曲线图

根据图 3(a)、图 3(b)所示的条件 Lyapunov指数的计算结果可知，当信息信号的幅度分别为A =10.0和A =100.0时，取k =10.95，两个系统能够达到混沌同步。首先在无噪声的情况下进行保密通信仿真，A=10.0数值仿真结果如图4所示（A =100.0的仿真结果图略）。由图4所示，信息信号得到了无失真恢复，且发射信号相对于信息信号已完全改观，这就证明设计方案是有效的。

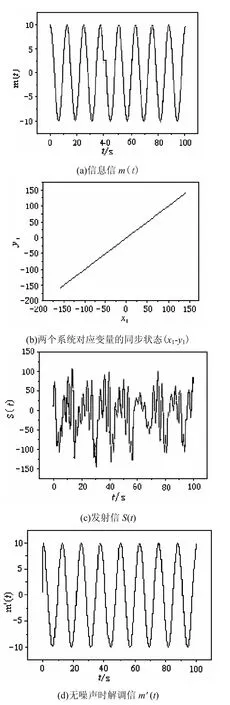
图4 信息信号m(t)=10.0cos(0.5t)

式中(0,1)σ为零均值，宽度为1的随机噪声，r为噪声强度。叠加噪声后信号解调结果分别如图 5（a）和图 5（b）所示。图(5a)示出了传输信号 m(t)=10.0cos(0.5 t)时，信噪比为22 dB时信号的解调结果 m"(t)，图 5（b）示出了传输信号

考虑到这些过程时是以理想信道为前提的，然而信号在实际传输过程中往往会受到信道噪声的干扰，稍大的噪声就会严重地影响到通信的质量。为了证明本方法对噪声有一定的鲁棒性，对有噪声的情况进行了分析和讨论，研究了发射端信号叠加性噪声的情形。即：m(t)=100.0cos(0.5 t)时，信噪比为 32 dB时信号的解调结果m"(t)。由图5可见，信息信号得到了很好的恢复，提出的方法具有一定的抗噪声能力。

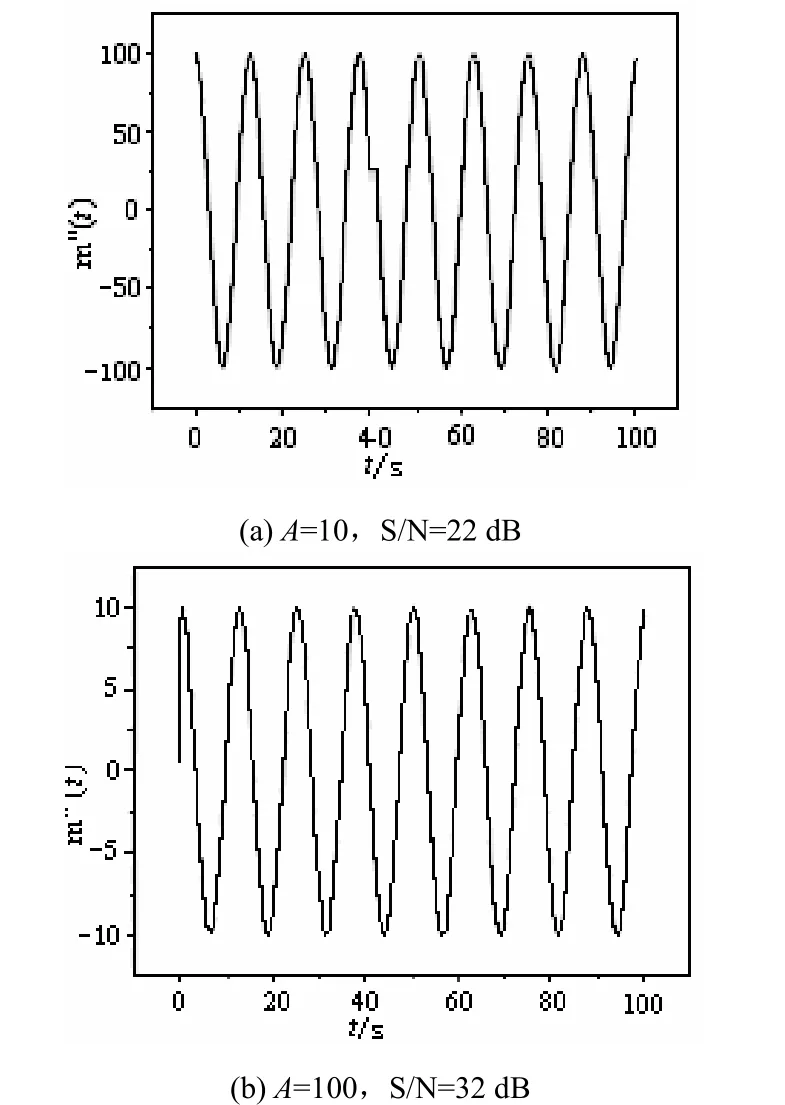
图5 加入噪声后的解调信号m"(t)

3 结语

在通信中，为了防止信号被破译和得到无失真恢复，要求接收系统与发射系统同步建立时间较短[5]。利用线性和非线性混合反馈实现超混沌系统的同步，且同步前的暂态过程较短。同时，通过采用信号的注入式通信方式设计混沌通信系统，使有用信号与混沌信号融合在一起，增强了系统的保密性，提高了传送有用信息信号的能量和通信的效率，且信号恢复失真小，因而使得这种保密通信方案适用于工程实践，有一定的实用价值。

[1] 韩春艳.一个产生复杂PR序列的自动切换混沌系统[J].通信技术，2009,42（06）：105-107.

[2] 赵耿，方锦清.现代信息安全与混沌保密通信应用研究进展[J].物理学进展，2003,23(02)：212-255.

[3] 关新平,范正平,陈彩莲,等.混沌控制及其在保密通信中的应用[M].北京：国防工业出版社,2002：5-7.

[4] TAMASEVICIUS A，NAMAJUNAS A，CENYS A. Simple 4D Chaotic Oscillator[J]. lectron Lett，1996，32(11)：955-957.

[5]马军,蒲忠胜,黎锁平.一类超混沌系统的广义同步研究[J].电路与系统学报，2007(04)：20-23.