溃坝的残余风险及风险评估

胡苏萍

（南京水利科学研究院,210024,南京）

一、溃坝的残余风险

要确保壅水建筑物的安全，不仅需要按照公认的技术规范进行设计、施工、运行以及安全监测，还必须采取技术、管理和组织措施实施残余风险管理。德国自1997年起开始对DIN 19 700∶1986壅水建筑物标准进行修订，历时7年，最终于2004年发布新修订的标准。DIN 19 700∶2004采纳了上述综合和透明的安全概念，除要求按规定完成设计和安全验证之外，还要求重视超过设计和验证极限的情况。在标准的第10部分明确指出，必须对因为超过设计洪水流量或洪水水位以及超过设计地震而造成的壅水建筑物安全的残余风险进行评估，并结合当地条件通过附加的、建设性的、管理和/或组织措施充分降低残余风险。这一要求表明：①壅水建筑物不可能达到100%绝对安全；②不是要排除风险，而是要降低风险；③必要时要采取预防事故的措施；④保留可接受的残余风险。按照DIN 19 700∶2004必须针对极端地震和极端洪水两种危险情况，对大坝失事的残余风险进行评估。

二、溃坝情景的建立

对已建坝进行风险评估的第一步就是要建立假定的溃坝情景。溃坝时间进程主要取决于大坝类型，土石坝与砌筑坝的溃坝特性不同，拱坝可能会突然间完全崩溃，而土坝渐进式侵蚀过程可能会持续数小时，充分认识历史溃坝事件将有助于选择符合实际的溃坝情景。

大坝形成溃口的原因各不相同，但不同的原因也可能导致溃口形状相似。表1总结了砌筑坝可能的溃坝原因及其相应的溃口形状。管涌和漫顶会导致土石坝溃决，而由地震或塌方造成边坡或坝体破坏引起土石坝溃坝的情况则较为少见。

根据不同原因造成的溃坝情景可以推算出溃口大小及溃口形成时间，这两个参数对于出流过程线具有决定性影响，可以利用由历史或试验得出的经验关系式确定，部分采用物理试验方法。表2给出了不同坝型的溃口参数和溃决历时经验值，考虑到这些经验值固有的不确定性，建议就不同的溃口参数（如宽度、深度和形成时间）进行敏感性分析。

近年，基于物质输移方程利用数值方法计算土坝溃口形成的可能性显著增大，但欧盟IMPACT项目2005年的研究结果表明，计算值与原型值或试验值之间仍然有30%～50%的偏差，尤其是溃口最大出流量。堆石坝的溃坝特性显然不同于土坝，虽然堆石坝能较长时间地经受住漫顶和渗流，但实际的溃坝进展较快，致使最大出流量较大。

如果不了解坝体中的内部结构（如防渗心墙或上游护面）对溃坝过程的影响，就很难作出正确的估算。对土坝的试验研究表明，与均质土坝相比，设有防渗心墙的土坝遭受侵蚀的速度较快，因为耐冲蚀心墙构成一个溢流堰顶，在它的后面紊流加剧，从而使冲蚀增强。关于防渗护面对溃坝过程的影响尚未进行研究。

砌筑坝溃坝被描述为突然失事，自19世纪以来，溃坝事件时有发生，为此加强了相关的理论和试验研究。砌筑坝溃坝后，溃口不再随时间产生进一步变化。如果把溃坝作为自由落体运动来考虑，就可以估算出取决于坝高的砌筑坝假定溃坝的最短时间。

针对一座由土坝和相邻的圬工坝（设有溢洪道）组成的壅水建筑物建立了相应的溃坝情景（表3）。在此情况下，尤其不具备足够的抗震安全性。尽管有泄降限制，但仍然考虑了壅水位快速泄降，因为误操作可能会导致出现上述情形。根据特定荷载出现概率与特定荷载下实际发生溃坝概率的乘积，确定各种溃坝情景出现的总概率。

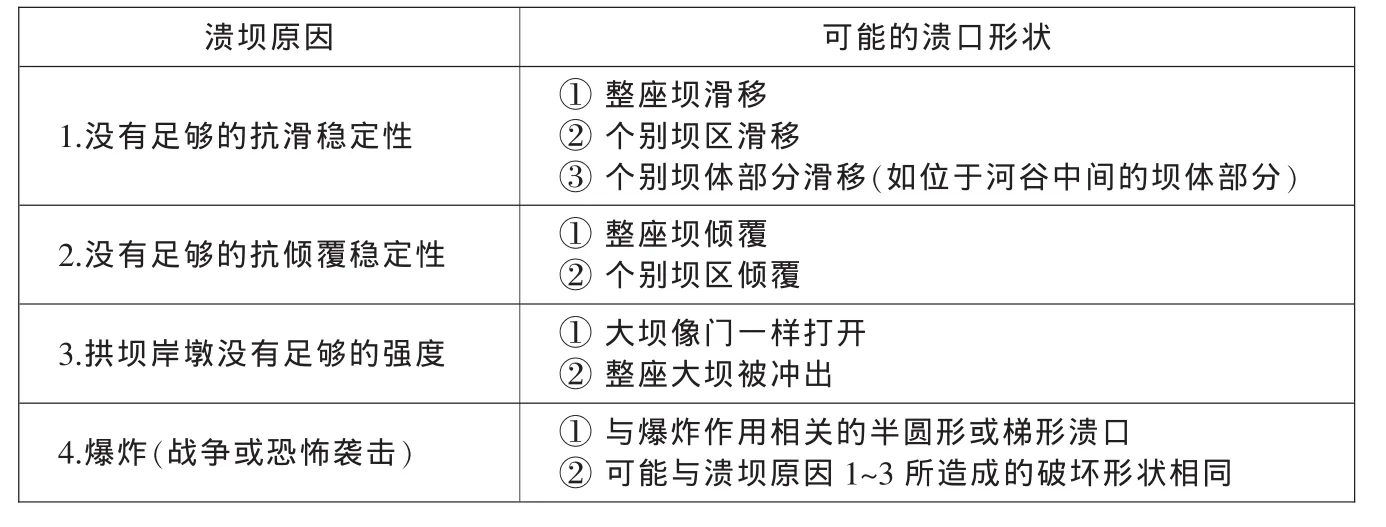
表1 砌筑坝溃坝原因及其相应的溃口形状

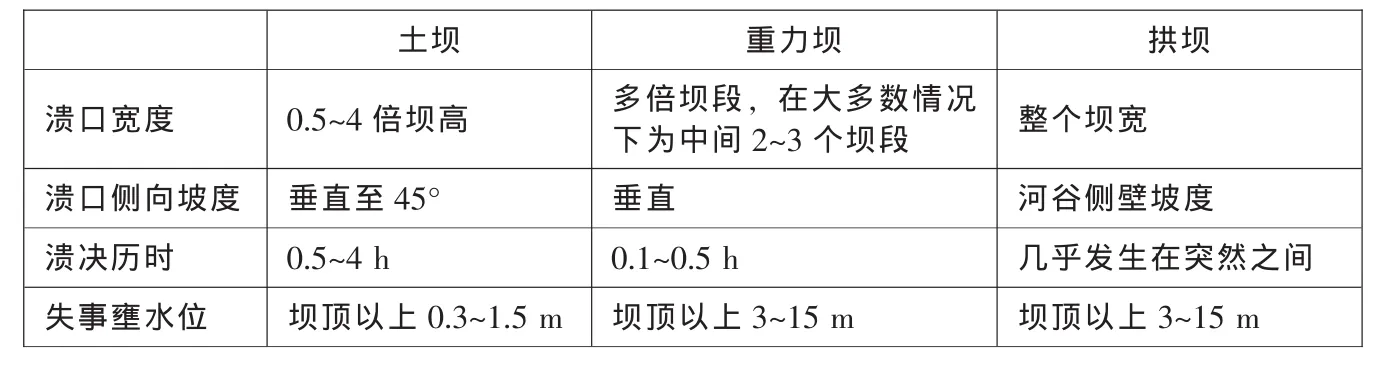
表2 不同坝型的溃口参数和溃决历时

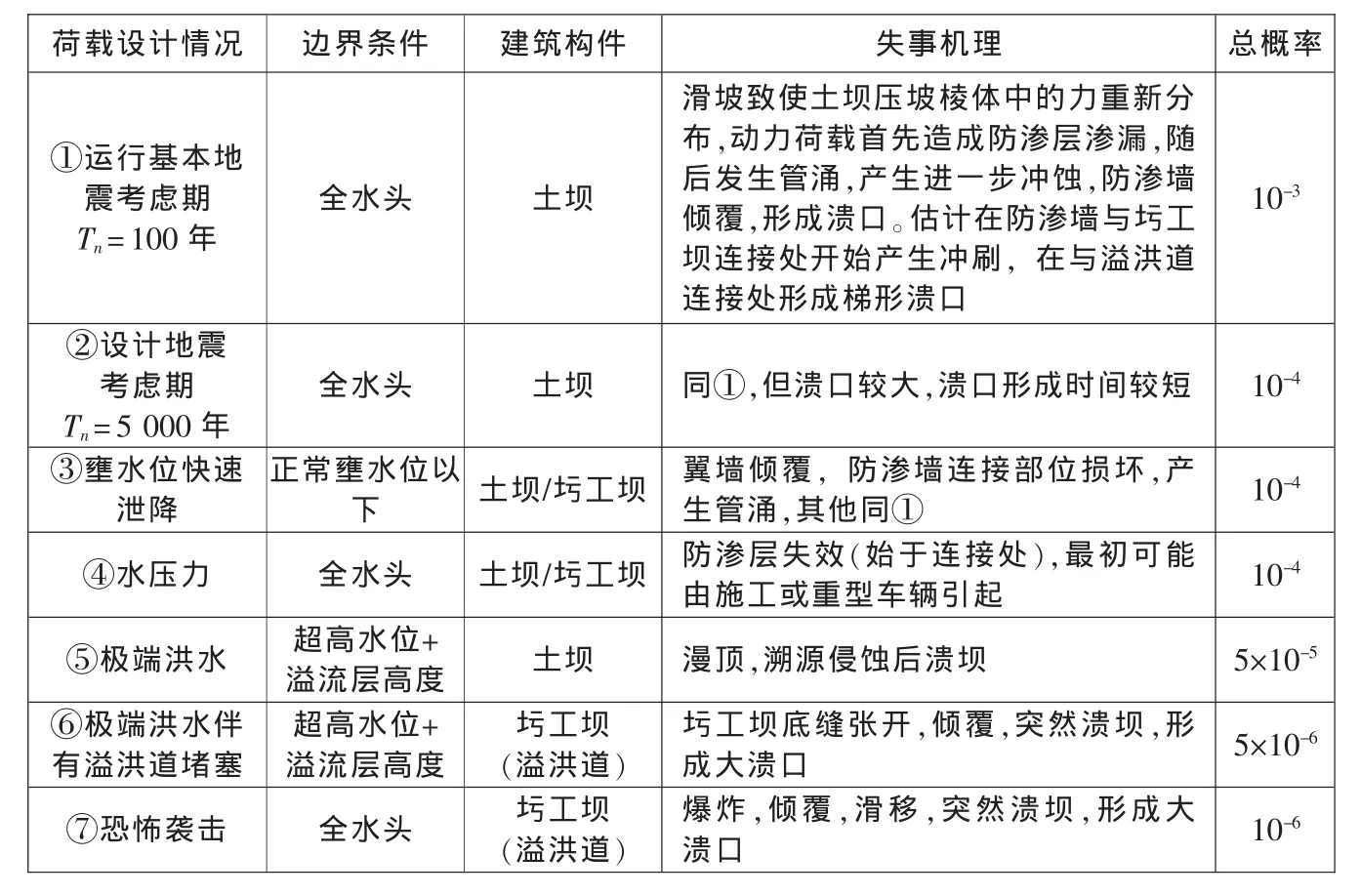
表3 由土坝和圬工坝组成的某壅水建筑物可能的溃坝情景

三、出流过程线的确定

要确定出流过程线，首先必须确定所研究情况下可能的水库初始水位，该水位对确定最大出流量具有决定性意义。在表3所列举的示例中，在大多数情况下考虑为大坝全水头。

根据已获得的Ritter解可以确定砌筑坝突然溃坝时的最大出流量，Ritter解的推导以平底无阻无限长矩形河道为基础，该值已通过不同试验在很大程度上得到验证，因此可以将其作为最大可能出流量应用于突然溃坝、近似矩形溃口的实际溃坝情景。

土石坝一般不会像砌筑坝那样瞬时全溃，土石坝溃决可以理解为一个溃口随出流量逐渐扩大的过程。初始溃口形成之后开始的水库泄放过程导致土石坝产生溯源侵蚀，这与出流量和水流拖曳力有关，因此溃口形成过程取决于筑坝材料抗侵蚀稳定性和水流特性。如果估算出最终溃口尺寸和溃口形成时间，也可以根据宽顶堰流计算出流过程线，堰宽就相当于溃口底部宽度，另外还需要其他一些参数，如水流收缩系数、溃口发展规律等，可以简化假设溃口均匀地加深和拓宽。

图1所示为针对示例坝计算的出流过程线，在图中将过程线沿x轴推移，使流量峰值总是在t=0的位置。为便于洪水波计算，按照出现概率对过程线进行总结和简化，用点线绘出简化过程线，并标出每年达到或超过该最大洪水流量的概率。

四、溃坝洪水波传播与危险图

与强降雨和融雪引起的洪水波不同，溃坝波传播速度显然更快，而且最大洪水高度更高，这两个特点也使这些现象的数值模拟更为困难。从历史溃坝事件来看，溃坝洪水波的传播速度为 5～65 km/h。

用于溃坝波计算的一维或二维数值计算模型以圣维南方程组为基础，推导时简化假设表面曲率可以忽略不计。尤其对波峰而言，这一假设似乎没有反映实际情况，然而测量结果与计算结果的比较表明，圣维南方程组虽然不能描绘波峰形状，但却可以正确地计算波峰传播速度。

在欧盟CADAM项目框架中，对法国Malpasset拱坝溃坝洪水波的比较计算表明，在采用相同的斯特里克尔系数情况下，与二维程序相比，一维程序所计算的溃坝洪水波速度较快，其原因在于一维程序未考虑流经弯曲河谷所造成的速度损失。对于弯曲河谷，选用一个较小的斯特里克尔系数更为合理，从而对河谷弯曲造成的洪水波减速沿传播路径平均予以考虑。

针对所研究的河谷选择一个合适的斯特里克尔系数对于淹没区范围的计算结果具有决定性影响。采用较低的斯特里克尔系数时（谷底高糙率）洪水波明显减速，较为平缓，因而洪峰流量显著减小；同时在斯特里克尔系数较低时，相应于特定流量的水位增大。应当根据糙率系数的敏感性分析确定上述两种相反的作用对于所计算淹没区的影响。

高糙率使洪水波减缓，流速降低，同时致使水位增高。而在城市复杂的道路系统中，公路和铁路上的流速则较大，在建筑物密集处流速减小，因此洪水波抵达城市某些地点的时间早于计算值。只有通过深入的研究和成本较高的二维或三维计算才能提供详尽的说明。

有些国家通过法律对溃坝计算作出了相应的规定，例如法国对洪水波传播的计算值设定了安全系数。将最大洪水波高度提高15%，将抵达时间缩短15%，这是根据敏感性分析和从实际考虑所作的修正。

初步估算时，可以根据过水断面的阻塞度推导出过滤（排水）速度与平均空隙速度的比值，这与多孔介质中的情形相似。可以粗略假设，在持久抵御洪水波的建筑物阻塞度为1%～50%的水流条件下，采用斯特里克尔糙率系数kst=15 m1/3/s的自由断面所计算出的速度要增加1倍。

溃坝洪水波的计算结果可用于建立风险图，为防灾部门制定应急预案提供依据。在危险图中可以标出可能的淹没区以及可达到的最大水深，还应通过有关溃坝情景、溃坝洪水波抵达时间、出流过程线和水位等说明对危险图进行补充。如果采用二维程序进行计算，也可用矢量图表示流速。要确保危险图不仅可以通过计算机调用 （GIS，利用口令从互联网下载），而且还要提供传统的纸质危险图，以防止停电或网络中断。

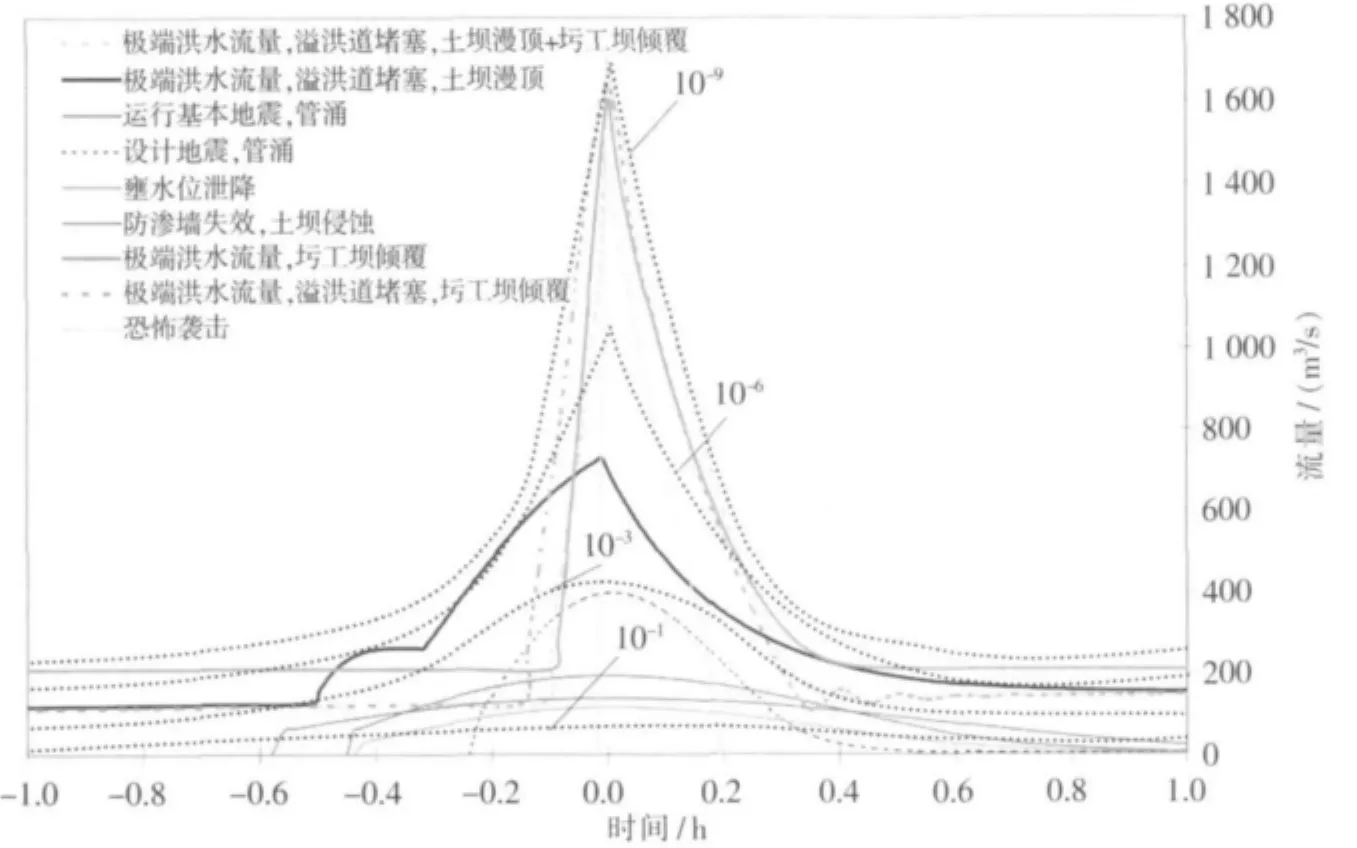
图1 特定溃坝情景（表3）的出流过程线与简化过程线

若要在特殊危险图中标明强度，可将局部水深与流速的乘积作为动荷载。若要建立风险图，应当标明溃坝出现的概率。频发的高强度洪水危害较大，即风险较大；而溃坝虽然危害强度高，但因为出现概率低，所以溃坝风险一般较小。

五、结 语

基于溃坝后果的严重性，有必要认识溃坝可能造成的影响，以便采取相应的预防措施，如建立预警系统或制定应急预案。鉴于大坝残余风险的研究一方面可通过对大坝溃口形成时间和与此相关的出流过程线进行推算，另一方面可通过对下游洪水波传播及其影响进行描述，并利用计算结果建立危险图。由于在计算假定中包含许多模糊变量，因此一张危险图只能描述一种特定的溃坝情景。根据各种不同的边界和初始条件可以建立各自相应的危险图。今后洪水波研究的另一种途径就是应用统计方法，并在事件图中标绘出特定水位的超越线。为最大程度地降低溃坝的残余风险，有必要不断引入新的大坝安全管理理念和科学技术方法，开展深入细致的研究。

[1]Bettzieche V.Das Restrisiko eines Talsperrenbruchs aus Betreibersicht[J].Wasserwirtschaft,2009,99(6):10-14.

[2]Pohl R,Bornschein A.Risikoabschtzung für einen theoretischen Talsperrenbruch [R].Interpraevent 2008—Conference Proceedings,Vol.1.2008.187-197.

[3]Bornschein A.Die Ausbreitung von Schwallwellen auf trockener Sohle unter besonderer Beruecksichtigung der Wellenfront [J].Dresdner Wasserbauliche Mitteilungen,2006,(33):1-255.

[4]郭军.欧美国家近期溃坝研究及发展动向[J].中国水利,2005(4).