平行接地大导体板间线电荷的电场分布

王福谦

（长治学院 电子信息与物理系，山西 长治 046011）

平行接地大导体板间线电荷的电场分布

王福谦

（长治学院 电子信息与物理系，山西 长治 046011）

利用复数坐标系z上的保角变换及镜像法，计算两平行接地大导体板间线电荷所形成电场的电势和场强分布。

导体板；长直线电荷；保角变换；镜像法；电势分布；场强分布

文献[1]运用保角变换法讨论了两平行接地大导体板间线电荷的电场分布，但因变换函数的局限性，仅计算出了线电荷到两导体板距离相等时所形成电场的电势和场强的分布，而没能给出线电荷位于导体板之间任意位置时电场分布的一般规律。本文将通过线性换、指数变换及余弦变换，利用镜像法得出线电荷在该区域的电势分布和场强分布，并绘制出其等势线和电场线图。

1 电势与电场强度

设在相距为a的两相互平行无限大接地导体板之间，充以介电常数为ε的均匀介质，平行于两导体板放置电荷线密度为λ的长直线带电体，该带电体到一导体板的距离为b（b＜a），因垂直于长直线带电体的所有截面上的电场分布都相同，故可取任一截面为z平面来讨论电势和场强在其上的分布，如图1所示。因为指数函数可将z平面上0＜Imz＜π水平带域变换为w平面的上半平面，并进一步变换为单位圆，所以，为了使用保角变换法计算z平面上电势和场强的分布，可先作如下的线性变换：

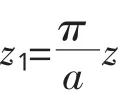
这样，z平面上两无限大导体板间的水平带形域0＜Imz＜a就映射为z1平面上的水平带形域0＜Imz＜π，如图2所示。

图1 变换前的水平带形域0＜IMz＜a

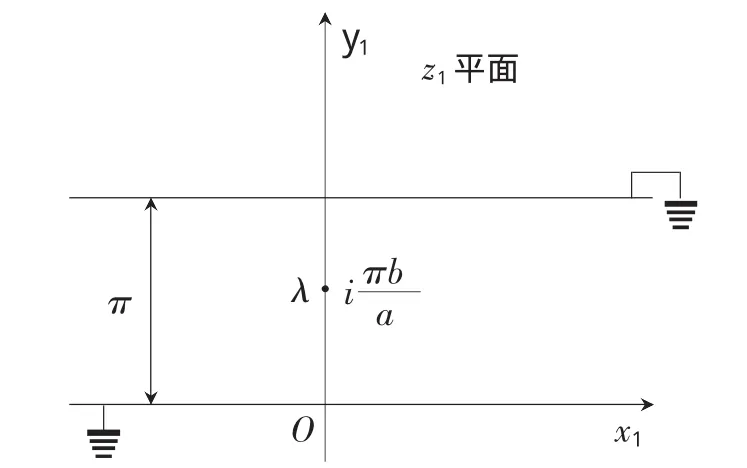
图2 变换后的水平带形域0＜IMz＜π

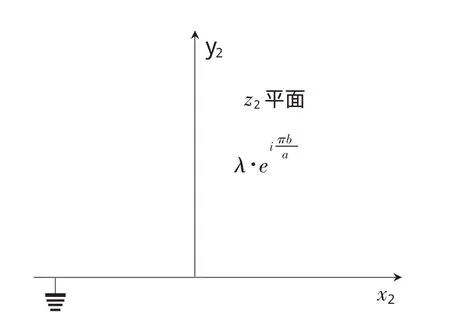
图3 变换后的上半平面一

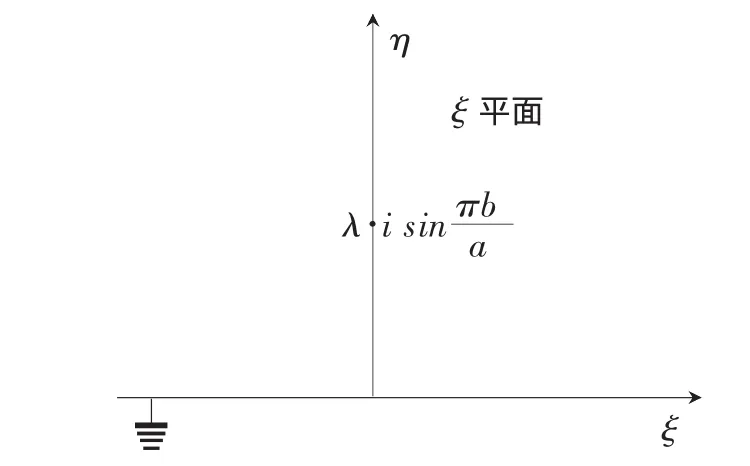
图4 变换后的上半平面二

再作变换z2=ez1，可将水平带域0＜Imz＜π变为上半平面Imz2＞0，如图3所示，线电荷位于z2=e处。最后作变换ξ=z2-cos，又将上半平面一变换为上半平面二，且电荷位于虚轴上的ξ=i sin处，如图4所示。综上所述，总变换为：

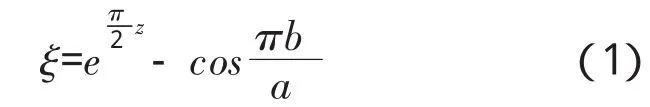
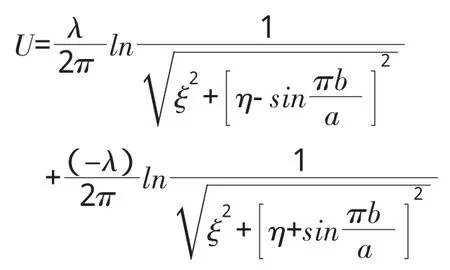
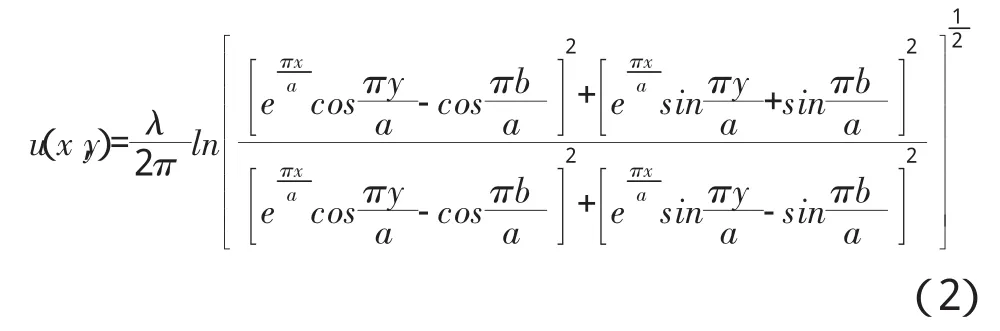
式（2）为长直线电荷在两平行接地大导体板之间的电势表达式。式中-∞＜x＜+∞，0≤y≤a。

由电势与场强的微分关系E=-▽U，得：

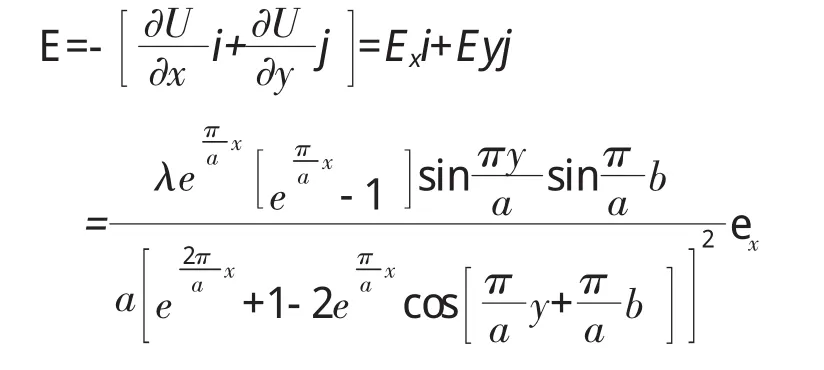
式（3）为长直线电荷在两平行接地大导体板之间场强的矢量表达式。

2 等势线与电场线函数

令式（2）中的 U（x，y）=C′，即令

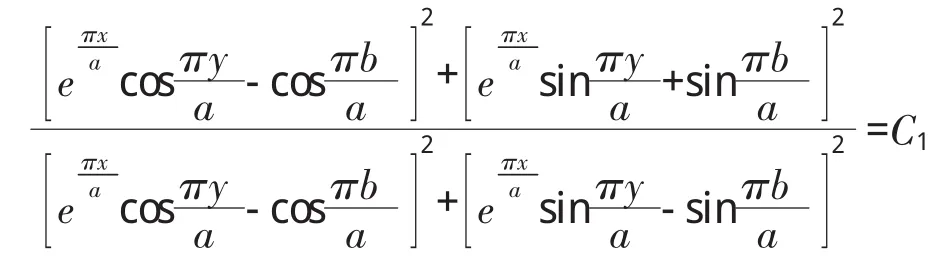
为正常数，（C1为正常数），可得等势线方程为

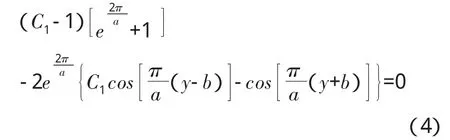
对于一个二元调和函数，若把它看作某解析函数的实部（或虚部），利用柯西-黎曼方程可求出相应的虚部（或实部），而对式（2）有=0说明U为一调和函数，若将U作为解析函数的实部，通过构造一个解析函数可求得其虚部E，而在oxy 平面上，U（x，y）的等值线族与 E（x，y）的等值线族是处处正交的。注意到平面静电场的等势线族与电场线族也是处处正交的事实，而U（x，y）为被解释为平面静电场的电势，则E（x，y）的等值线就是该静电场的电场线族。利用柯西-黎曼方程，由得：

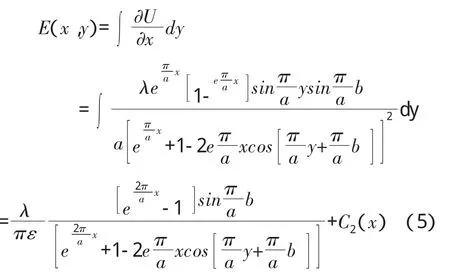
由上式得 C′2（x）=0，则可确定 C2（x）=C2=常数。

故得长直线电荷在两平行接地大导体板之间的电场线函数为：

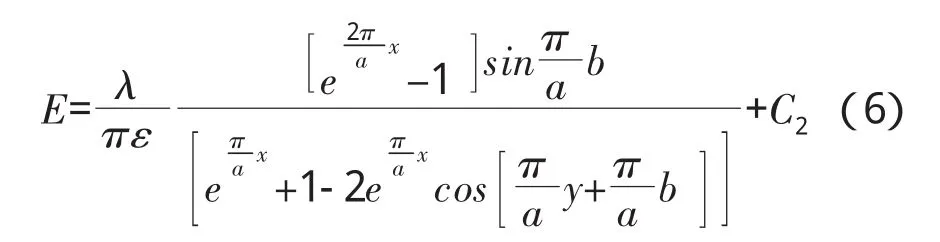
图5为通过软件MATLAB绘制出的长直线电荷在两平行接地大导体板之间的电场线和等势线图（a=1.5，b=0.5）。图中箭头所示为电场线族，实线为等势线族。

图5 电场线和等势面图

3 结束语

两平行接地无限大导体板为一物理模型，当接地板的线度比起其间距离大得多时，两接地板可看作为无限大。本文中得到的关于长直线电荷在两平行接地大导体板之间的电势和场强分布的结论具有一定的参考价值，一些实际场合都可用此来做近似估算。

［1］王福谦.两平行接地大导体板间线电荷的电场［J］.大学物理，2008，27（12）：26-28.

［2］胡嗣柱，等.数学物理方法解题指导［M］.北京：高等教育出版社，1997（2005重印）94-96.

Abstract：This paper is intended to calculate the electric potential distribution and electric field intensity distribution of line charged between parallel ground connection Conductor board by using mirror method and the conformal mapping on the coordinate systeMof the complex number.

Keywords：conductor plate；a line charged；conformalmapping；mirrormethod；electric potential distribution；electric field intensity distribution

（责任编辑 王璟琳）

Further Calculation of the Electric Field of Line Charged Between ParallelGround Connection Conductor Plate

WANG Fu-qian
（Department of Electronic Information and Physics Changzhi University，Changzhi Shanxi 046011）

TM26

A

1673-2014（2010）05-0033-03

2010—09—23

王福谦（1957— ），男，山西运城人，副教授，主要从事大学物理教学与研究工作。