D-S证据理论的不足及其数学修正❋
2010-09-11陈炜军景占荣袁芳菲朱安福
陈炜军,景占荣,袁芳菲,朱安福
(1.西北工业大学电子信息学院,陕西西安 710072;2.南昌市第十九中学,江西南昌 330003)
0 引 言
传感器技术的快速发展带动了多传感器信息融合技术的迅速发展,多传感器信息融合关键在于信息融合所处理的多传感器信息具有更复杂的形式,而且通常在不同的信息层次上出现.多传感器系统中,各传感器所提供的信息都具有一定程度的不确定性,对这些不确定信息的融合过程实质上就是一个不确定的推理过程.不确定性推理逐渐成为信息融合的关键.
D-S证据理论因其完备的数学基础,通过对事件的概率加以约束以建立信任函数而不必说明精确的难以获得的概率,能方便地处理由“不知道”所引起的“不确定”而成为不确定性推理中最常用的方法之一,在多传感器信息融合中得到广泛应用;但它本身也存在一些不足,不仅体现在它对参与融合的各传感器所提供证据信息的独立性要求,更体现在它对相互冲突的证据信息进行融合出现违反直觉的悖论上.关于如何改进阻碍证据理论进一步广泛应用的证据独立性的条件,一些学者有专门的文献论及,这里不作讨论;而本文是从后面一点来论及 D-S证据理论存在的不足,对证据理论的相应改进方法进行了有效的分类、归纳和总结,并在此基础上提出了一种新的用于 D-S证据理论的修正
1 D-S证据理论及其存在的不足
D-S证据理论是由 Dempster于 1967年提出的,他首先提出了上、下界概率的定义,后由 Shafer于1976年加以推广和发展,使之成为符合有限离散领域中推理的形式,并使之系统化、理论化,形成了一种不确定性推理的理论,即 D-S理论[1].证据理论讨论一个识别框架 Θ,它是关于命题的相互独立的可能答案或假设的一个有限集合.按传统方法可以把Θ的幂集表示为 2Θ,它是Θ的所有子集的集合,D-S证据理论对这个识别框架Θ进行运算,并提供计算Θ中所有幂集元素的逻辑,然后使用这些计算结果完成对命题的高和低的不确定性表示[2].
D-S证据理论的基本概念,文献 [3]有详细的论述,本文不再赘述.其理论的核心是 Dempster证据组合规则,现将其介绍如下.
Dempster组合规则:设 m1,m2,…,mn是识别框架 Θ上的基本概率分配函数(BPFA),则多概率分配函数的正交和 m=m1⊕m2⊕…⊕mn由式(1)表示

例 1 设识别框架Θ={A,B,C},现有两条证据如下:m1(A)=0.99,m1(B)=0.01,m1(C)=0;m2(A)=0,m2(B)=0.01,m2(C)=0.99.根据 D-S证据理论所得的数据如表 1所示.
从表 1数据可以看出,不一致因子 k=m(Ø)=0.0099+ 0.9801+0.0099=0.9999,接近于 1,两条证据高度冲突,合成之后各命题基本概率赋值为:m(A)=0,m(B)=1,m(C)=0.可见,两条证据各支持 A和 C,但融合后的概率均为 0,同时对 B的支持程度由融合前的 0.01变为 1,此后即使增加再多的证据,无论它们对 A,C的支持率多高,对 B的支持率多低,融合结果 A,C始终为 0,产生与常理相悖的融合结论,出现“一票否决”现象.

?
出现该问题的原因是因为 D-S证据理论规定 m(Ø)=0,而在不同证据组合的过程中得到的空集Ø的概率事实上并不为 0(如表 1中数据所示);但在组合的过程中 D-S方法却舍弃了这部分概率的值,只是通过乘以归一化系数 1/(1-k)来对组合后的有效基本概率值进行补偿.
2 D-S证据理论的相关改进
针对上述悖论的出现,为了解决证据高度冲突情况下多传感器信息的有效融合问题,众多研究人员为此作了大量的分析研究,提出了不少改进方法,但这些改进方法无外乎两种思路,一种是对 Dempster组合规则进行修正,另一种则是对冲突证据源进行修正.依据这两种思路可以把这些方法分为两大类:一类是认为 Dempster组合规则有问题,需要修改组合规则,典型的如 Yager[4]方法、Lefevre[5]方法、孙全[6]方法、李弼程[7]方法、向阳[8]方法等;另一类则认为组合规则没有问题,而是给出的证据源需要修改,典型的如 Murphy[9]方法、徐凌宇[10]方法、梁昌勇[11]方法、邓勇[12]方法等.而实际上,问题出现的关键原因是各证据源间冲突信息的存在,各种改进方法都是关于冲突信息的分配或预处理的方法.
2.1 D-S证据理论的第一类改进 组合规则的修正
第一类解决方法的代表是 Lefevre等人提出的统一信度函数组合方法.Yager,Lefevre等人认为,证据理论对冲突信息组合出现悖论的原因就是 Dempster组合规则本身不完善所导致的,对冲突信息必须按一定规则重新分配,这种分配又面临两种需要解决的问题[12]:①冲突应该重新分配给哪些子集;②在确定可接收冲突的子集后,冲突应该以什么比例分配给这些子集.事实上,Dempster组合规则不能处理高度冲突的信息的原因就是对冲突信息全部抛弃的结果.
Yager提出的改进方法[4]采用对冲突信息重新分配的原则,把支持证据冲突的那部分概率全部赋予未知领域,而对于不冲突证据仍采用 Dempster组合规则的与运算方式进行合成.Yager证据合成公式为

式中:k与式(1)定义一样;Θ为辨识框架;Ø为空集.即把冲突认为是对客观世界的无知部分,将冲突信息全部划分给全域即未知项Θ,等待新的证据来临再做判断,符合认知逻辑,并且解决了高度冲突的证据的合成;但由于 Yager对冲突证据 k是全盘否定的,全部赋给了未知项,因而在证据源多于两个时,合成的效果并不理想(见本文例 2).
孙全针对 Yager合成公式的问题,在文献 [6]中提出一种改进方法,认为即使证据间存在冲突,它们也是可用的,而不应全部分配给未知项,并通过引入了证据可信度X的概念,对冲突性证据 k采用加权和平均的形式进行分配.孙全证据合成公式为

李弼程针对证据可信度X的主观随意性,在文献 [7]的合成公式中废弃了证据可信任度的概念,把支持证据冲突的概率按各个命题的平均支持程度加权进行分配.其合成公式为

式中:q(A)为各证据对命题 A的平均支持度,与式(3)定义一致.
在对 D-S证据理论的第一类改进(即对 Dempster组合公式的改进)中,以上的式(2)~(4)都起到了较好的积极作用,能够较合理地处理高冲突证据的融合,但均未考虑对各证据交叉情况下融合作用的改进.向阳在文献 [8]中提出了反映证据交叉融合程度的聚焦系数 s1的概念,根据所联合的集合的基数大小决定向下聚焦的程度,防止在大的子集上(携带确定信息不多)的基本概率分派函数聚焦在小的子集上.向阳的合成公式为

但该合成公式只适用两路证据合成,对多路证据合成则无能为力,而且聚焦系数 s1等于证据集合基的比例,属于一种线性平均运算关系,违背了 D-S证据理论不冲突性证据“与运算”的合成法则,因而这种合成法则同样也不完善.
2.2 D-S证据理论的第二类改进 证据源的修正
第二类解决方法的代表是 Murphy的方法.Murphy,Haenni等人认为,D-S证据理论有完善的数学基础,其组合规则是没有问题的,问题出在冲突的证据源上,需要通过修改降低冲突信息量后,再利用Dempster规则进行组合.更进一步,Haenni[13]从工程实践的角度指出,各种对 Dempster组合规则的改进并没有降低系统的计算量,且这些改进方法不满足结合律,将导致工业应用的困难;此外,当证据数量成百上千时,如何确定冲突分配的子集并不像理论分析那样简单.因此,以他们为代表提出了对证据源修正之后再利用 Dempster规则进行组合的思想.
Murphy[9]基于对冲突证据源修正的思想,提出一种对证据源平均的方法,在证据组合之前,将所有证据进行平均,即系统有 n个证据时,直接将证据的基本概率指派进行平均后使用 Dempster组合规则组合 n-1次.该方法只修改组合证据源,而组合规则不变,保留了 Dempster组合规则的交换律和结合律,且融合实验证明 Murphy的方法所得的结果要好于直接运用 Dempster组合规则所得到的结果,能够融合高度冲突的证据.但 Murphy方法只是一种朴素的平均思想,其将各个证据源等同看待,每个证据源的权重都是一样的,所以这种证据源信息分配的思想并不完全合理.
针对这种现象,徐凌宇引入有效因子λ[10]来衡量证据源的可靠性,并将其引进信任函数,所有的证据经过有效性评估后再进行组合.梁昌勇则引入专家的权威T[11]的概念,T通过已知的经验得到,各条证据通过乘以不同的权威系数T1,T2,…,Tn进行折中.这两种方法都在一定程度上解决了 Murphy方法中各证据源权重分配一致的问题,但同时带来一个新问题——λ和T的值都需要先验的知识来获取,这在专家系统中可以通过对专家的统计评价综合得出,但在多传感器系统融合中λ或T值的给出带有太大的主观随意性,因此他们的方法只是一种特定环境下证据源修改的思想,在普适意义上并没有解决 Murphy方法中存在的问题.
邓勇在文献 [12]中通过引入 Jousselme[14]等人定义的“距离函数”概念,来度量证据体间相似性程度,并进一步获得系统中各个证据被其它证据所支持的程度,通过对支持度归一化处理得到各条证据的可信度,作为证据的权重,对多源证据进行加权平均后再利用 Dempster组合规则融合证据信息.该方法不同于文献 [10-11],利用的是证据源本身携带的信息来确定各证据的权重,且继承了 Murphy方法的所有优点,是一种很好的证据源修改思想.但该方法从证据源提取特征信息之后,对原证据全盘抛弃,只对组合后得到的平均信息源进行操作,这样做虽然使得证据融合的收敛速度加快(朝证据支持的概率大的命题快速收敛),但并不妥当,容易造成弱势信息的丢失,对要求第二判决的应用不利,并且计算量较上述方法大.
3 D-S证据理论的一种新的修正模型的提出
从上面的论述可以看出,以 Yager为代表的 D-S证据理论组合规则的修正和以 Murphy为代表的D-S证据理论证据源的修正分别代表了 D-S证据理论完善的两种方向.从哲学思维的观点来看,例 1中证据理论出现的问题可以描述为用 U方法解决模型 V,得到了违反直觉的结果 W,Yager等人认为方法U出了问题,而 Murphy等人认为是模型 V出了问题.他们分别从不同的角度对其进行了解决.事实上,这恰恰是一个问题的两个方面:这个不合常理的结果 W既有可能是方法 U不完善,也有可能是模型 V出了问题,还有可能是 U和 V都有问题,就像光的“波粒二象性”一样.因此,基于这样一种哲学认识,本文试着同时对方法 U和模型 V进行修正,并考虑证据交叉融合时的情况,在文献 [7,12]的基础上引入证据信息容量 e(E)的概念,提出了一种用于 D-S证据理论修正的新模型.
定义 1[15]一条证据 E的信息容量 e(E)可以定义为

式中:‖◦‖表示集合的基数(即集合中元素的个数);g(Al)是焦元集 Al的个数.显然有 0≤e(E)≤当 m(Ai)=0时,e(E)=0;若 m(Ai)=1,且‖ Ai‖ =1时,则 e(E)=1.
定义 2 证据源修正规则如下,即通过各条证据的信息容量对焦元交叉的证据作折扣.

定义 3[14]Θ为一包含 N个两两不同命题的完备识别框架;m1,m2为Θ上的两个基本可信度分配函数,则 m1,m2之间的距离可表示为

式中:m表示定义在幂集 2Θ上的以 m(Ai)为元素的列向量;D为一个 2N×2N阶的矩阵,其中的元素为
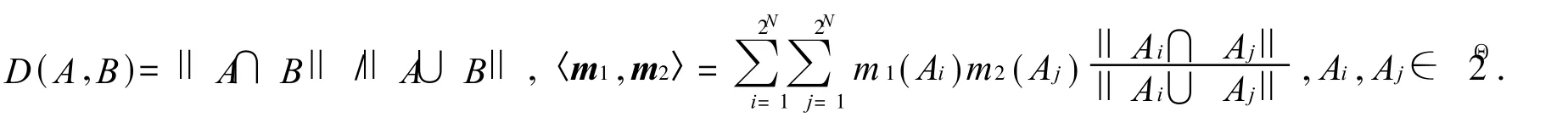
定义 4[12]证据体 mi和 mj之间的相似性测度 sim(mi,mj)为

定义 5[12]证据系统中证据体 mi的可信度为
定义 1指出了一条证据 E的信息容量与其焦元集中所含元素的个数有关,若该证据各焦元集均只含有一个元素,则该证据的信息容量 e(E)=1,其所包含的有用信息最多.根据信息容量可以对焦元集发生交叉的各证据作折扣,进行证据源(合成前的各条证据)的修正,在一定程度上解决了焦元信息交叉的各条证据间的去相关问题.
定义 2给出了一种新的证据源的修正规则,该规则通过证据体内在的信息容量对证据各焦元集的基本概率赋值进行重新分配,并保证了概率分派的完备性.
定义 3,4,5是根据文献 [15]的方法,通过引入证据体间的距离函数实现各证据在证据系统中可信度的分配,解决了对 DS证据理论作第一类修正的各种方法对参与合成的各证据一视同仁的做法,使出现冲突的证据对整个证据系统信息合成的影响最小化.
在定义 1,2对证据源修正的基础上,考虑证据可信度分配的不同,提出如下新的证据合成公式

4 数值实验及比较
为了验证本文组合公式的融合效果,下面以两个数值实验进行仿真计算,并将仿真结果与几个典型文献的方法作分析比较.
例 2 设识别框架Θ={A,B,C},现有 4条证据如下:
E1∶m1(A)=0.98,m1(B)=0.01,m1(C)=0.01;E2∶m2(A)=0,m2(B)=0.01,m2(C)=0.99;E3∶m3(A)=0.9,m3(B)=0,m3(C)=0.1;E4∶m4(A)=0.9,m4(B)=0,m4(C)=0.1.将 6个合成公式的融合结果作对比分析,其融合结果如表 2所示.

表2 各论据公式融合结果对比表Tab.2 Contrast list of fusion result for each evidence formula
从融合结果可以看出,本文方法优于 D-S和对 D-S理论做第一类改进的方法,因为本文方法按各证据在整个证据系统中的可信度对冲突部分的信息加权进行分配,取消了文献 [6]中主观随意性大的证据可信度X的概念,且比文献 [7]的方法更合理.该例中,各证据‖ Ai‖ =1,所以 e(Ej)=1,m′j(Ai)=mj(Ai),k′=k,所以当各证据焦元独立不交叉时,运用本文方法证据源无需修改,同时得到了与 Murphy方法和邓勇方法相近的结果.尽管在证据系统中证据达到 4个时,m(A)的收敛速度要慢于这两种方法,但没有丢失第二命题 C的信息.当识别框架所含焦元数较多时,在保证快速融合做出第一判决的情况下,对需要作出第二判决的应用更有利.
再来看证据焦元的基数不全都为 1的情况,与文献 [8]中的方法进行比较.
例 3 设识别框架 Θ={A,B,BC,D},现有 3条证据如下:E1∶m1(A)=0.9,m1(BC)=0.1;E2∶m2(B)=0.1,m2(D)=0.9;E3∶m3(A)=0.9,m3(B)=0.1.现将本文方法和文献 [8]向阳的方法进行证据间融合,结果对比如表 3所示.

表3 焦元基不为 1的证据融合结果列表Tab.3 Fusion result list of evidences whose aggreg ative cavdinal number isn′t1
从上面这个例子可以看出,在证据冲突较小(k较小)的情况下,本文修正模型所得融合结果和文献[8]的结果很接近,融合效果相当,具有相当“s1”的向下聚焦的程度,只不过在证据焦元基数不为 1时,本文公式把不属于证据信息量的那部分概率赋给了未知项,从融合结果看这样做也是合理的.而在证据冲突较大(k较大)的情况下,本文方法所得结果和文献 [8]的结果就截然不同了.尽管证据 E1和 E2对命题B的支持率都非常低,文献 [8]的合成结果支持 B,而对 A和 D,包括它们的并集却没有任何的支持;而文献 [8]对证据 E2与 E3的合成结果更是只支持命题 B,这明显是有悖常理的 — 既然两个证据几乎各支持一个命题,那么,这两个命题合成以后对该命题的支持率都应接近 0.5.本文提出的修正模型合成公式更好地吻合了这个结论.
5 结束语
本文提出的 D-S证据理论的修正模型是在前人工作的基础上研究得出的,在分析现有改进方法的基础上,通过引入证据信息容量和证据可信度来对各传感器提供的证据信息进行预处理,既包括了 Dempster组合规则修正的思想,又包涵了证据源修正的思想,并将它们进行了较好的结合,是一种对 D-S证据理论进行修正的新思路.由上面数值实验的融合结果比较可以看出,按照原始的 D-S推理、几种典型的改进方法和按照本文修正方法所得到的结果并不一样.本文公式方法不仅很好地解决了证据信息冲突情况下的信息融合,可以更好地剔除无效证据信息的干扰,融合结果符合常理和逻辑判断,在一定判决门限下可以使信息融合的结果更快速、更合理,而且较文献 [8]更有效地解决了证据信息交叉(证据焦元基数不全为 1)时的融合情况,是一种好的融合算法.
这种证据的组合算法可以在决策支持、多传感器决策级数据融合等方面具有很好的应用前景.比如在多传感器数据融合中,来自不同传感器的可靠性存在很大差异,而这种可靠性又是在主观不可预知的情况下,运用该算法可以有效地降低和抵消个别传感器因偶然因素带来的“坏值”的影响,将引起冲突的证据信息(“坏值”)通过整个证据系统对其的支持程度(证据可信度)将其降到最小,从而有效地保证融合结果的可靠性和准确性.但相比较而言,当一个稳定的证据系统有新的证据信息加入时,该算法需要重新计算各证据在整个证据系统中的可信度,所需的计算量较大,如何有效地简化计算量和提高融合速度需要今后进一步的深入研究.
[1]Shafer G.A Mathematical Theory of Evidence[M].Princeton:Princeton University Press,1976.
[2]Dubios D,Prade H.A survey of belief revision and updating rules in various uncertainty models[J].International Journal of Intelligent Systems,1994(9):61-100.
[3]康耀红.数据融合的理论与运用 [M].陕西:西安电子科技大学出版社,1997.
[4]Yager R.On the dempster shafer framework and new combination rules[J].Information Sciences,1987(41):93-137.
[5]Lefevre E,Colot O,Vannoorenberghe P.Belief function combination and conflict management[J].Information Fusion,2002,3(3):149-162.
[6]孙全,叶秀清,顾伟康.一种新的基于证据理论的合成公式 [J].电子学报,2000,28(8):117-119.Sun Quan,Ye Xiuqing,Gu Weikang.A new combination rule of evidence theory[J].Acta Electronica Sinica,2000,28(8):117-119.(in Chinese)
[7]李弼程,王波,魏俊,等.一种有效的证据理论合成公式 [J].数据采集与处理,2002,17(1):33-36.Li Bicheng,Wang Bo,Wei Jun,et al.An efficient combination rule of evidence theory[J].Journal of Data Acquisition&Processing,2002,17(1):33-36.(in Chinese)
[8]向阳,史习智.证据理论合成规则的一点修正[J].上海交通大学学报,1999,33(3):357-360.Xiang Yang,Shi Xizhi.Modification on combination rules of evidence theory[J].Journal of Shanghai Jiaotong University,1999,33(3):357-360.(in Chinese)
[9]Murphy C K.Combining belief functions when evidence conflicts[J].Decision Support Systems,2000,29(1):1-9.
[10]徐凌宇,尹国成,宫义山,等.基于不同置信度的证据组合规则及应用 [J].东北大学学报,2002,23(2):123-125.Xu Lingyu,Yin Guocheng,Gong Yishan,et al.Combination rules of various credibility evidences and application[J].Journal of Northeastern University,2002,23(2):123-125.(in Chinese)
[11]梁昌勇,陈增明,黄永青,等.Dempster-Shafer合成法则悖论的一种消除方法 [J].系统工程理论与实践,2005(3):7-12.Liang Changyong,Chen Zengming,Huang Yongqing,et al.A method of dispelling the absurdities of dempstershafer’s rule of combination[J].Systems Engineering-Theory&Practice.,2005(3):7-12.(in Chinese)
[12]邓勇,施文康,朱振福.一种有效处理冲突证据的组合方法[J].红外与毫米波学报,2004,23(1):27-32.Deng Yong,Shi Wenkang,Zhu ZhenFu.Efficient combination approach of conflict evidence[J].Journal of Infrared Millimeter Wave,2004,23(1):27-32.(in Chinese)
[13]Haenni R.Are alternatives to Dempster′s rule of combination real alternatives?:Comments on “ About the belief function combination and the conflict management problem” [J].Information Fusion,2002,3(4):237-239.
[14]Jousselme A L,Grenier D,Bosse E.A new distance between two bodies of evidence[J].Information Fusion,2001,2(1):91-101.
[15]李剑峰,乐光新,尚勇.基于改进型 D-S证据理论的决策层融合滤波算法[J].电子学报,2004,32(7):1160-1164.Li Jianfeng,Yue Guangxin,Shang Yong.Decision-level fusion filtering algorithm based on advanced D-S theory of evidence[J]Acta Electronica Sinica,2004,32(7):1160-1164.(in Chinese)
