基于损伤的混凝土梁的承载力研究

陈燕，杨智良

（滁州职业技术学院土木工程系，安徽 滁州 239000；安徽农业大学工学院，安徽 合肥 230036）

基于损伤的混凝土梁的承载力研究

陈燕，杨智良

（滁州职业技术学院土木工程系，安徽 滁州 239000；安徽农业大学工学院，安徽 合肥 230036）

混凝土的破坏过程是其内部开裂的微裂纹逐渐发展，损伤力学 中的连续变量场即损伤场能够描述微裂纹的发展，文中将损伤引入到混凝土梁的承载力计算，计算结果表明，混凝土梁的真实承载力比不考虑损伤时大为降低。

混凝土；损伤；承载力

混凝土在现代建筑工程中是应用最为广泛的材料之一，长期以来，人们对混凝土材料和构件宏观力学性能的裂化直至破坏全过程的机理、本构关系、力学模型和计算方法都非常重视，进行了大量的研究。取得了许多成果，形成了一整套混凝土结构的分析和设计方法。而混凝土无论在先天形成过程中还是后天使用过程中都会不可避免的存在微缺陷或微裂纹，这些微缺陷或微裂纹又由于一系列的外界因素影响扩展为宏观裂纹而影响其力学性能[1，2]。这与传统的强度理论假设材料处处连续，毫无裂纹相悖。大量的科研学者进行了实验、理论研究。许多研究己经证明了混凝土的破坏是其内部开裂的微裂纹逐渐发展的结果，要想真正描述混凝土材料及其结构的某些特性和现象，分析结构的使用寿命和安全可靠性，就必需研究其内部微缺陷的演化规律。损伤力学将这些微缺陷和微空隙的力学作用理解为一个连续变量场即损伤场，并由此来研究微空隙微缺陷的发展规律，进而研究带有微缺陷的材料或者结构的力学特性和强度特性[3]。

一、基于损伤的混凝土本构关系

混凝土材料内存在的损伤（微缺陷），可以看作连续的变量场（损伤场），而损伤的发展导致材料中弹性刚度的降低，弹性模量在材料损伤阶段亦随之降低。因此损伤可以用弹性模量的变化来描述。引入损伤变量，此时混凝土的本构方程变为[4，5]

其中uk是关于Cartesian坐标的位移分量。 为Kroneck三角常数

式（1）表明，损伤变量的作用相当于一个刚度减小因子。随着损伤的增加，有效刚度模量减小，直到D=1时，变为零。对于混凝土等准脆性材料[5]，损伤的演化律由下式确定

即有效应力和应变满足线性关系。在单向应力状态下又退化为

二、基于损伤的混凝土梁的承载力

一矩形截面纯弯曲梁由混凝土制成，如图1示，由于混凝土在成型过程中会留下细观缺陷，脆性材料抗拉性能差。加载后，在梁的拉应力区会形成连续分布的细观裂纹扩展，

图1含损伤的混凝土梁

Nc的作用点位于

Nt的作用点位于

由平衡条件Nc=Nt和Ncyc+Ntyt=M得

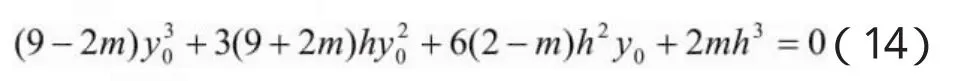
由式（1 4）可以解出梁的顶部和底部的应力

在不考虑材料损伤时，梁的承载力为

tu控制。当D=0.5时， ，因此式(1 8)可以写成(2 0)

由此可见，考虑损伤后，梁的承载力比不考虑损伤时的承载力降低了2 9.2%。

3算例

为了更进一步地验证损伤对构件承载力的影响，选择如图2所示一三点弯曲梁进行考虑损伤的有限元计算，并将计算结果与实验值进行比较。梁的尺寸为：2.0 m×0.1 m×0.2 m。采用二十节点等参单元计算。网格尺寸为1 0 0×1 0 0×5 0 mm3。

图2受集中力作用的梁的结构简图

损伤的演化采用指数软化法则，即M a z a r s模型[6，7]

式中 ， 为材料常数， 为损伤门槛值根据所选材料的软化曲线由试验点确定，等价应变由修正的V o n-M i s e s法则定义

其中v为柏松比，k为混凝土压缩-拉伸强度比，I1为应变张量第一不变量，J2为偏应变张量第二不变量。

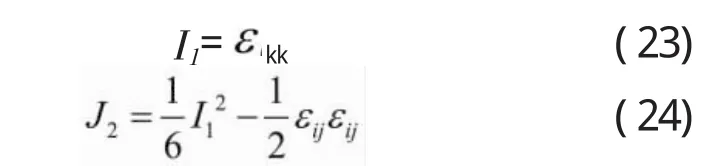
梁的荷载-位移曲线如图3所示。从图中可以看出，考虑损伤后的构件的荷载-位移曲线和实验结果基本吻合，也即考虑损伤后的构件承载力才是构件的实际承载力。

图3荷载-位移曲线

四、结论

混凝土是一种典型的非均匀准脆性材料，其失效过程实际上就是微裂纹萌生、扩展、贯通，直至宏观裂纹产生导致混凝土失稳破裂的过程。损伤力学通过引入损伤场的概念，研究微空隙微缺陷的发展规律，能够真实地反映混凝土构件真实的承载力。

在实际工程应用中，因为实际的材料、构件和结构中总会有一些空洞，微裂纹和微孔隙等各种各样的微缺陷，而以往的传统处理方法不考虑这些微缺陷的存在，将研究对象抽象为连续的无损伤的变形固体，其实际的承载力就会被高估，将损伤引入材料承载力的计算，才能真实有效地反映材料的实际承载力，具有很重要的工程意义和应用前景。

[1]赵启林，孙宝俊等.非局部损伤模型的客观性研究[J].工程力学，2003，（5）：185-189.

[2]刘军.混凝土损伤分析及其工程应用[D].辽宁：大连理工大学，2004.

[3]吴丽琴.单轴受压混凝土损伤的细观试验研究[D].广西：广西大学，2006.

[4]王学滨.考虑应变梯度及刚度劣化的剪切带局部变形分析[J].工程力学，2006，(10):101-106.

[5]李兆霞.脆性材料损伤应变率效应及其本构模拟[J].固体力学学报，1998，(4).

[6]Peerlings R H J， de Borst R， Brekelmans W A M and Geers M G D.Gradient-enhanced damage modeling of concrete fracture. Mech. Cohesive-Frictional Mat.，1998，3:323～342.

[7]Mazars J and Pijaudier-Cabot G， Continuum damage theory-application to concrete[J].J Eng Mech，1989，115:345-365.

book=59,ebook=30

TU528.57

A

1671-5993（2010）03-0059-03

2010-07-21

陈 燕（1976-），女，安徽明光人，滁州职业技术学院土木工程系讲师。

杨智良（1974-），安徽安庆人，男，安徽农业大学农业建筑与能源工程研究所所长，副教授，硕士生导师。