模型式教学——从一道计数模型谈教学

王大忠

（ 铜仁学院 数学与计算机科学系，贵州 铜仁 554300 ）

模型式教学
——从一道计数模型谈教学

王大忠

（ 铜仁学院 数学与计算机科学系，贵州 铜仁 554300 ）

排列与组合不仅是组合数学的最初步知识和学习概率统计的基础，而且也是日常生活中应用比较广泛的数学知识。在组合数学的教学过程中，我们采用数学模型教学来教授学生，使学生能更好地掌握组合数学的相关知识，激发学生的求知欲，使学生进入问题情境，从而产生好奇心，形成探究愿望。从一道简单的计数模型出发，研究了组合数学的模型式教学。

1．前言

在数学思想中，排列与组合这一数学思想在学生的后继学习中扮演重要的角色。由于组合知识在生活生产中应用的广泛性，在高中数学的学习中，学生就将学习组合数学的相关知识。因为其思维方法的新颖性与独特性，学习时要遵循“不重不漏”的原则，所以它又是培养学生思维能力的不可多得的好素材。

结合学生的年龄特点，可以适当在数学题中添加一些趣味模型元素，提高学生兴趣，在激发学生数学兴趣的同时，也让他们感受到数学的重要性。从生活实例出发到数学基础知识，正是现行教材的编排特点。作为数学老师，除了教会学生学懂书本知识，进而运用书本知识解决实际问题外，更多的是教给学生学习方法，启发学生的思维，激发学生学习兴趣。

先做如下符号说明[1] 。

2．相关数学定义

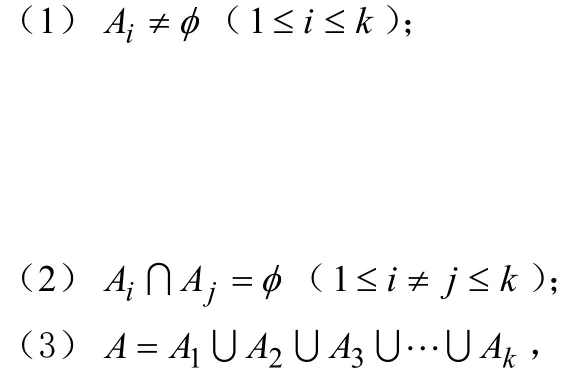
则称{ A1A2A3…Ak}是A的一个k分划，并记为

称Ai（1≤i≤k）为A的k分划（1-1）的一个块。

定义2 第二类Stirling数：一个n元集合的全部k分划的个数叫做第二类Stirling数，记作 S(n ,k )。

3．正整数的分拆

定义3 正整数的分拆：正整数n的一个k分拆是把n表示成k个正整数的和

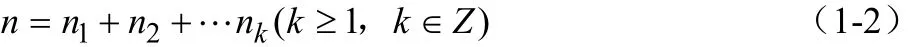
的一种表示法，其中 n1>0(1≤i ≤k )叫做该分拆的分部量。如果表达式（1-2）是无序的，也就是说，对诸ni任意换位后的表示法都视为同一种表示法，这样的分拆叫无序分拆，或者叫分拆，我们把n的k分拆记为 B(n ,k )。

基本定理[2]1：一次不定方程 x1+x2+…+xr=n的非负整数解的组数为：其中r、n是正整数。

推论1：如果正整数n >r，r也为正整数，那么一次不定方程的正整数解的组数是：或

证明：将不定方程 x1+x2+…+xr=n 化为

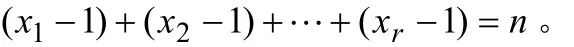
令 yi= xi−1，则yi≥0(i = 1,2,… ,r )，代入上式得到不定方程： y1+y2+…+yr=n−r 。

因为n-r是正整数,故据基本定理1可知：不定方程

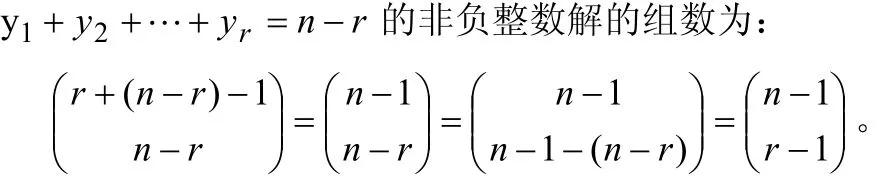
若注意到 yi= xi−1≥0，即 xi≥1 ,便可知不定方程的正整数解的个数是：或

4．计数模型问题

例：把n个完全不同的球放到r个完全不同的盒子里面，并且允许有空盒，问共有多少种分配的方案数？

分析：这里把n个球放到r个盒子里，而且允许有空盒，那么也就是说必须把每个球都放到一个盒子里，则一个球有r种不同的放法，那么n个球就有种不同的放法。即共有nr种分配方案。

小结：这个例题的模型共受三个条件的约束，

（1）小球是否相同；

（2）盒子是否相同；

从而，接下来将要讨论改变这些条件，让不同的条件组合在一起，看看有什么新的问题产生？这些问题又和哪些知识联系在一起？解决这些问题的方法是什么？

4．1．模型一

把n个完全不同的球放到r个完全相同的盒子里面，并且不允许有空盒，问共有多少种分配的方案数？

分析：在这里我们将这n个不同的小球看作是一个n元集合，记为 A={x1，x2，…，xr}，将A划分为r个非空子集，记为Ai(i = 1,2,… ,r )。然后将每个Ai(i = 1,2,… ,r )放到一个盒子里，构成一个没有空盒的分配方案。

这里模型一的问题就可以看作：对于n元集A的r个非空集合Ai(i = 1,2,… ,r )，由于每一个盒子（子集）都必须装有至少一个小球，并且小球不同，所以装好小球后，集合A的每两子集中都不出现相同的元素（小球），即： Ai≠φ（1≤i≤r），且 Ai ∩ A j =φ（ 1≤i≠j≤r ）。而此时A恰好可以表示为：，这个是满足定义1的，所以我们的一种分配方案就对应集合A的一种r分划。那么我们的全部分配方案数就是集合A的全部r分划的个数，这是满足定义2的，所以模型一的分配方案数共有 S(n ,r )种。

模型一就是集合的分划与第二类Stirling数的数学模型，这是生活中实际存在的问题，可以帮助学生加深理解集合的分划与第二类Stirling数的定义。接下来我们在模型一的基础上改变条件。

4．2．模型二

把n个完全不同的球放到r个完全不同的盒子里面，并且不允许有空盒，问共有多少种分配的方案数？

分析：要解决模型二这个问题，首先来观察一下模型一与模型二的关系，看看他们有什么相似和不同的地方。

对照组:开腹手术。患者气管插管全身麻醉,于下腹正中或耻骨联合上做切口,进腹后,根据肿瘤部位、性质、体积,游离,完整剔除肿块,钳夹输卵管、卵巢系膜,以可吸收线缝合剩余的正常卵巢及系膜并结扎,待肿瘤切除干无残留,腹腔无出血后,关闭切口。

模型一与模型二它们只是盒子相同与否的情况不同，由于模型二中的盒子是不相同的，那么模型一中的一种方案对于模型二来说就有r!种（和顺序有关），而模型一共有 S (n ,r )种，那么模型二就有 S (n,r)⋅ r!种。

4．3．模型三

把n个完全不同的球放到r个完全相同的盒子里面，并且允许有空盒，问共有多少种分配的方案数？

分析：同样我们观察模型一与模型三有什么不同和相似。

模型一与模型二的差异只是允不允许有空盒，模型一是不允许有空盒，模型二是允许有空盒，那么模型三是否可以转化为模型二的情况呢？回答是肯定的。在模型三中我们把装好小球的盒子（非空）k (k = 1,2,… ,r )个拿出来，不考虑空的盒子。那么模型三就转化为：把n个完全不同的球放到k（k=1，2，…，r）个完全相同的盒子里面，并且不允许有空盒，问共有多少种分配的方案数？这正好是模型一的情况，只是盒子的数目不同罢了，则这样的方案数有 S(n ,k )种。那么在模型三中共有这样的情况r种，则模型三的方案数为

4．4．模型四

把n个完全相同的球放到r个完全相同的盒子里面，并且不允许有空盒，问共有多少种分配的方案数？

分析：由于不允许有空盒，且盒子是相同的，所以r个盒子中每一个都至少有一个小球，而且放好后和盒子的顺序无关，只算一种方案。

设第i (i = 1,2,… ,r )个盒子有ki（ ki≥1，ki∈Z ）个小球，则： n =k1+k2+…kr，ki（ ki≥1，ki∈Z ）。对于任意的正整数n，这恰好满足定义3。在模型四中，由于盒子是相同的，那么就和盒子的顺序无关，即： n =k1+k2+…kr，ki（ki≥1，ki∈Z ）是关于正整数n的一个无序分拆，那么模型四的方案数就是正整数n的r分拆数的个数：B(n, r)。

4．5．模型五

把n个完全相同的球放到r个完全相同的盒子里面，并且允许有空盒，问共有多少种分配的方案数？

模型五与模型四的不同点在于是否允许有空盒。我们仿照前面的方法，将模型五的空盒去掉不看，只看装好的盒子，设有k (k = 1,2,… ,r )个盒子装了小球，那么现在模型五就转化为：把n个完全相同的球放到k (k = 1,2,… ,r )个完全相同的盒子里面，并且不允许有空盒，问共有多少种分配的方案数？易知，该问题就是模型四的情况，那么其方案数为B (n, k )，而模型五有r个这样的情况产生，即 k =1,2,… ,r ，那么模型五的方案数总共有：

4．6．模型六

把n个完全相同的球放到r个完全不相同的盒子里面，并且允许有空盒，问共有多少种分配的方案数？

设第i (i = 1,2,… ,r )个盒子有ki个小球，盒子是允许空盒的，所以ki满足： ki≥0，k∈Z 。又因为盒子互不相同，所以必须考虑盒子的顺序问题，也就是说对于模型六的一种方案，就应该对应正整数n分成r个分部变量的一个有序分拆：

的一个非负正整数解（ k1， k2，…， kr），相当于将k1个小球放到第一个盒子里，将k2个球放到第二个盒子里，……，将kr个小球放到第r个盒子里。

由定理1知：模型六的总的方案数也就是不定方程（1-3）的非负整数解的组数：

4．7．模型七

把n个完全相同的球放到r个完全不相同的盒子里面，并且不允许有空盒，问共有多少种分配的方案数？

对照模型六的方法，把问题转化为求解不定方程：x1+x2+…xr=n的正整数解（ k1，k2，…， kr）的组数。

根据定理1的推论1及其证明可知：

模型七的总的方案数为：

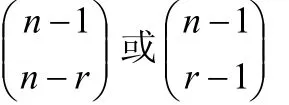
5．总结

知识本身是严肃的，但当人们加以运用时，便会生发许多的情趣来，由严肃变为活泼、幽默、亲切、有趣。在教学中，如果我们在传授知识的同时以模型点缀，则会使学生体验到知识之乐趣，这不仅有助于理解，而且有助于记忆和运用。我们要让学生感觉到数学知识并不都是抽象的，而是生活中需要的，蕴含着生活中的乐趣，这也反映了学习知识的必要性。因此，我们如果在教学中善于采用模型，就会使学生体验到知识的乐趣。

模型式教学模式是在新形势发展下而提出的，适应当今教学发展的要求。常言道，教学是一门艺术，正因为是艺术，教师在教学中根据具体知识的特点及学生的实际来创设模型就尤为重要。因此，只要教师在教学中认真贯彻启发式教学思想，一切从实际出发创设问题情境，注重模型教学，就一定能使教学质量得到提高。

[1] 孙淑玲，许胤龙．组合数学引论[M]．合肥：中国科技大学出版社，

2008．

[2] 张炳汉．关于不定方程整数解计数问题的讨论[J]．天中学刊，2001，（5）．

[3] 王春香，李玲．《组合数学》教学指导[J]．高等函授学报（自然科学版），2003，16（6）．

[4] 曹炜萍．数学中的趣味教学[J]．科技文汇·数学教学，2009-1（下旬刊）．

[5] 张景中，吴鹤龄．幻方及其他[M]．北京：科学出版社，2005-3．

[6] 孙侠，殷志祥等．“组合数学”课程教学规律探索[J]．今日科苑，2008，（20）．

[7] 徐建兵，李明山．《有趣的搭配》的教学设计、反思及评析[J]．网络科技时代，2008，（7）．

[8] 高洁．浅谈组合数学的应用与教学[J]．中国科技信息，2005，（15）．

Model Teaching from Teaching from a Counting Model

WANG Da-zhong

( Department of Mathematics and Computer Science, Tongren University, Tongren, Guizhou 554300, China)

The arrangement and combination are not only the most preliminary knowledge of combination mathematics and the base of learning probability statistics, but also used widely in daily life. In the process of teaching combination mathematics, we use mathematical models to teach to let students can better grasp the knowledge of combination mathematicsl, stimulate their desire for knowledge, enable them to enter the problem situation, create their curiosity and form the desire of exploration. In this paper, the model teaching of combinatorial mathematics is researched beginning from a simple counting model.

model teaching of combination mathematics; set partition; the second kind of Stirling number; partition of positive integer; first-order indefinite equation （责任编辑 毛志）

A

1673-9639 (2010) 03-0128-03

2010-06-24

王大忠（1987-），男，贵州开阳县人，贵州省铜仁学院数学与计算机科学系学生。