低能He原子与Li2分子碰撞散射截面理论计算*

李劲令狐荣锋司冠杰杨向东†

1)(四川大学原子与分子物理研究所，成都610065)

2)(海南大学材料与化工学院，硅锆钛资源综合开发与利用海南省重点实验室，海口570228)

3)(贵州师范大学物理与电子科学学院，贵阳550001)

(2009年8月10日收到;2009年11月19日收到修改稿)

低能He原子与Li2分子碰撞散射截面理论计算*

李劲1)2)令狐荣锋1)3)司冠杰1)杨向东1)†

1)(四川大学原子与分子物理研究所，成都610065)

2)(海南大学材料与化工学院，硅锆钛资源综合开发与利用海南省重点实验室，海口570228)

3)(贵州师范大学物理与电子科学学院，贵阳550001)

(2009年8月10日收到;2009年11月19日收到修改稿)

利用Fuchs势模型和密耦方法对He-Li2碰撞体系低能散射截面进行理论计算，研究了He-Li2碰撞体系的散射总截面随能量的变化、微分截面随角度的变化、分波截面随总角动量的变化以及与入射能量之间的关系，并总结了量子效应随入射能量的变化规律.

密耦方法，微分截面，分波截面，Fuchs势模型

PACC:3440，3450

1. 引言

近几年来，随着理论研究的进一步深入，微观物质的相互作用越来越引起人们的关注，而原子分子之间相互作用的研究是最为重要的方面之一，尤其是原子和分子之间的相互作用势及他们之间相互碰撞时散射截面的变化规律，由于我们研究的散射截面是指振动和转动激发截面，因此它与激光物理、化学激光、化学反应动力学、天体物理等学科的发展都有着密不可分的关系［1，2］，不仅为这些学科的发展奠定了牢固的理论基础，而且起到了巨大的推动作用，在理论上把这些学科紧密地联系在一起的同时，为其交叉学科的出现和发展起到了举足轻重的桥梁作用.而原子与分子的碰撞转动激发又是碰撞问题的主攻方向，其在冲击波、声波、风洞扩张、气体激光器的研究设计、转动激发的共振荧光过程、星际空间物质的冷却过程、爆轰物理研究等方面也具有重要的物理意义［3—10］.

Li2分子和稀有气体原子之间相互作用势是近年来备受关注的研究课题.Fuchs和Toennies等人实验研究表明，He-Li2体系作用势受Li2分子振动能量影响，并在此基础上提出Fuchs势模型［11］，与键长相关的各向异性势能部分成为He-Li2体系的研究热点，Bodo等人的从头计算［12］、Rubahn和Bergmann等人的半经验势［13，14］，都是围绕着各向异性势能部分展开研究，Gianturco等人利用Fuchs势模型研究He-Li2体系非弹性碰撞的振转耦合作用［15］，Marques等人使用二维原子椭圆模型研究He-Li2碰撞的转动激发［16］，而Bodo等人用量子计算方法研究He-Li2碰撞去激发散射截面［17］.本文从Fuchs势模型出发，把密耦方法［18—25］应用在He-Li2体系中，利用相互作用势与散射截面的关系，分析其散射截面的变化规律.

2. Li2分子的势能面

对于大多数双原子分子来说，Murrell-Sorbie函数［26，27］的三阶与四阶力常数都与光谱值完全符合，是目前最好的势能函数之一，已广泛用于分子碰撞过程［28］，对Li2分子势能面我们采用Murrell-Sorbie函数的形式.由于绝大多数双原子分子和离子的电子态、光谱项通常能给出ωe，ωeχe，Be，αe和离解能D0，所以常采用五参数Murrell-Sorbie函数形式［26，27］，即

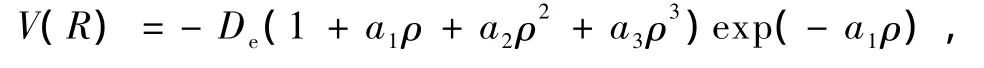
其中离解能De可由D0经零点能校正得出

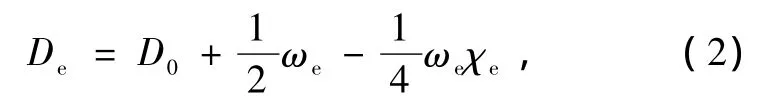
式中的参数a1，a2，a3之间的关系可由力常数f2，f3和f4确定，

相对于Li2的势能面而言，其参数如表1.

表1 基态Li2分子的Murrell-Sorbie势能函数的参数［26］

3. He与Li2的相互作用势

目前关于卤族元素的分子与原子的相互作用势是人们广泛关注和研究的对象之一，文献［11］中给出了两种势模型:Stahl和Staemmler模型及Fuchs和Toennies模型.

3.1. Stahl和Staemmler共同提出的势能表面模型

Stahl和Staemmler共同提出了Li2与He的相互作用势模型:当Li2的键长为re(re为分子处于平衡位置时的键长)且γ为0°和90°(γ是入射原子与靶分子轴之间的夹角)，此时势能的各向异性很小，可以使用两项勒让德把势能展开为

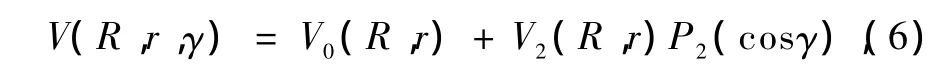
其中

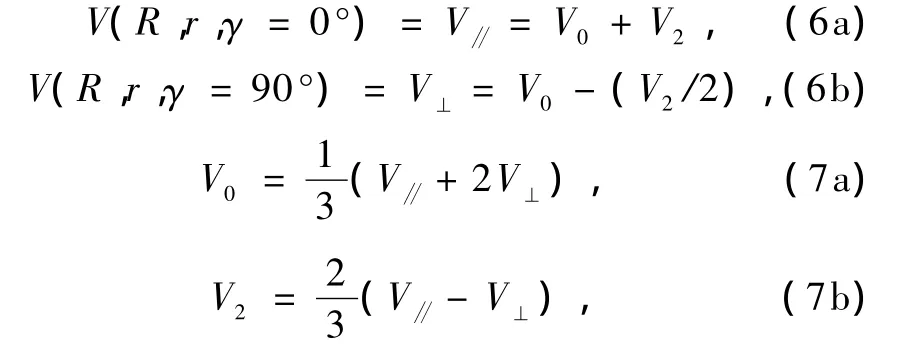
其中

在这里ρi=(R/Rmi－βi)/(1－βi)，对于Li2与He碰撞体取n=8和s=6已经足够了，不需要太大的值，ε为势阱的深度，Rm为势阱的位置，对于Li2与He碰撞体系而言，上面的参数取值如表2.

表2 Stahl和Staemmler势能参数

由于Stahl和Staemmler认为分子中原子间距没有变化(r=re)，即没有考虑Li2的振动，因此势模型不够完善.

3.2. Fuchs和Toennies共同提出的势能模型［11］

Fuchs和Toennies分析了Stahl和Staemmler势模型后，提出He-Li2体系的一种新的相互作用势，这种相互作用势由于包含了Li2分子中原子间距r的变化，考虑了Li2的振动，其对势能面的的描述也更为准确，他们也把He-Li2体系的势能分解为γ为0°和90°两种情况

其中

相对于基态的He-Li2体系而言，通常情况下我们取f=0.ε‖，ε⊥，Rm‖，Rm⊥，β‖，β⊥同表2和表3中给出一个基态和两个激发态的其它参数值.

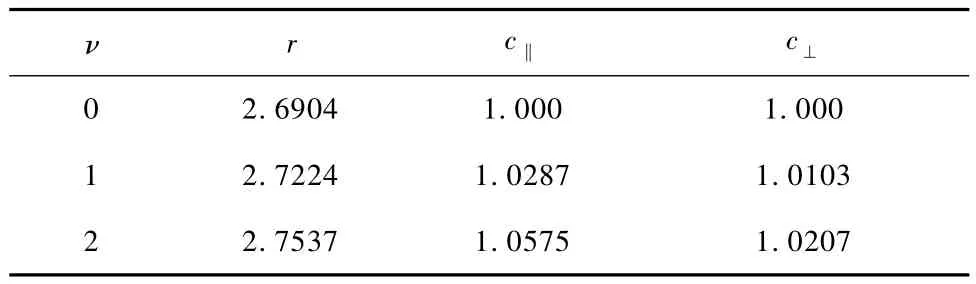
表3 Fuchs和Toennies势能参数

下面就这两种势能模型进行比较和分析:从图1和图2可以看出，两种势能函数的V0，V2在He原子与Li2分子的间距R较大时基本符合，但在R较小时他们间的差别明显有所增大，这是因为在修正的Fuchs势能中含有r的缘故，当Li2分子中原子的间距r变化时，即便R不变也会导致三体势的变化.我们选r=2.2，2.4，re，3.0，3.2分别作Fuchs势能曲线，与Stahl势能线比较，相同的R值，各向同性势能部分V0与各向异性势能部分V2均随r增大而变大，并随r减小而变小，但V2比V0变化较为敏感，而在r=re时两种势能模型一致.R较小时，若Li2键长r减小，Li2分子各向异性变小，与Li2键长相关的各向异性势能部分V2随之变小，反映出He-Li2体系相互作用势随Li2键长改变，可见经过修正的Fuchs势能形式较为准确.

图1 He-Li2体系Fuchs和Stahl势函数V0的比较

图2 He-Li2体系Fuchs和Stahl势函数V2的比较

4. 计算结果及讨论

当入射He原子能量E=0.001—0.11 eV时，用密耦方法和比较合理的Fuchs势模型计算了基态的He-Li2散射总截面、微分截面及分波截面，He-Li2散射总截面的计算结果表示在图3中.

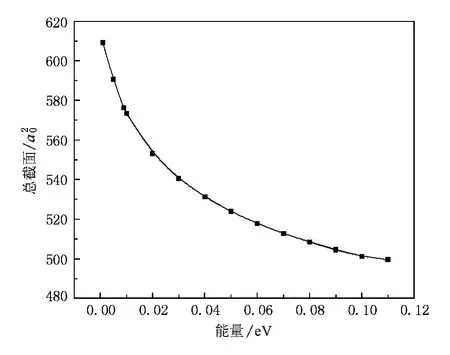
图3 He-Li2体系总散射截面随能量E的变化

从图3可以看出，随着入射能量的增加，散射总截面变得越来越小.这是因为当He原子向作为靶的Li2分子入射时，会受到Li2分子势能场的作用.相对于较低的入射能量而言，势能场对入射He原子的作用就显得较强，其散射率相对较大，随着能量的增大，散射率变小，散射截面也就变小.当入射He原子能量为0.078 eV时，散射总截面为510.1 a20，文献［11］的实验值为562.2 a20，文献［13］的计算值为642.2 a20，可见我们的计算结果更接近实验值.

在图4中绘出了He-Li2碰撞体系在入射能量为0.03 eV时的微分散射截面，图中曲线分别表示总微分截面、弹性微分截面和非弹性微分截面，从图中可以看出，随着入射角度增大，总微分截面和弹性微分截面都逐渐变小，而非弹性微分截面则变化不大.在0°—20°的范围内，经过了几次振荡后总微分截面、弹性微分截面都快速减小，而在20°之后它们的变化都趋于平缓，可见小角度微分截面的数值要比大角度微分截面的数值大得多，即在总微分截面和弹性微分截面中小角度散射概率比大角度散射概率要大得多，也就是说在散射过程中小角度散射是主要部分.

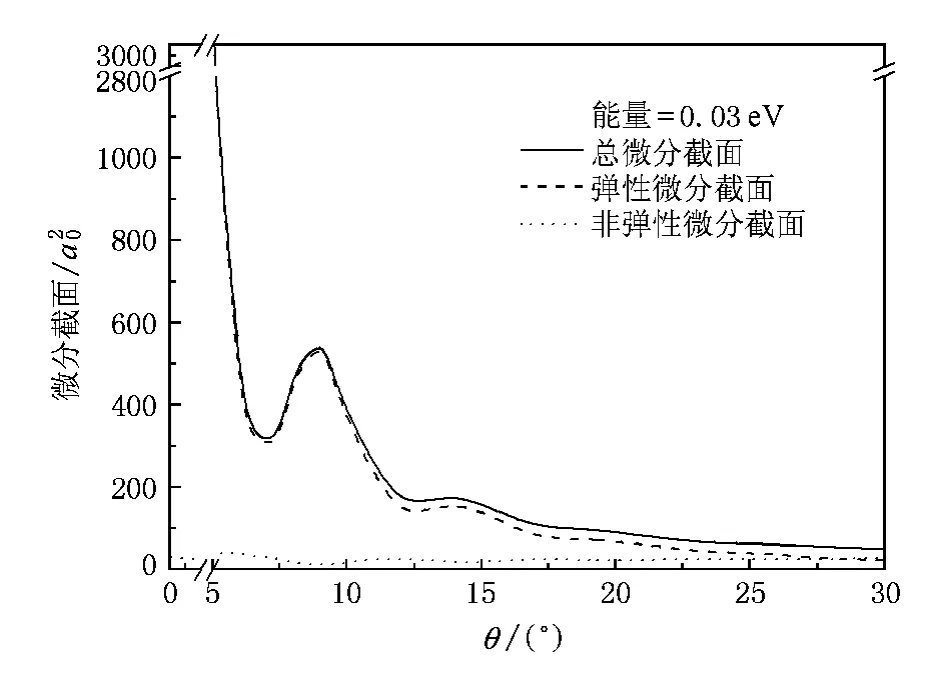
图4 He-Li2体系碰撞能量E=0.03 eV时的微分截面

图5绘出了入射能量分别为0.001，0.0075，0.02 eV时，分波截面与总角动量量子数J的关系，由图5可以看出，分波截面随着J的增大不断地振荡，当达到某一最大值后快速下降而趋于0，但是应该注意到的是对于入射能量为0.001 eV时在其最大值的后面又出现了一次振荡，这就是所谓的尾部效应(尾部效应是指当入射粒子的角动量大到在经典散射情况下已不可能与散射势场发生作用时，由于量子效应，粒子仍会受到势场的散射，在图中表现为分波截面出现一个最大的极值后又出现了一个较小的极大值，称为尾部效应).而在能量入射较高时，量子效应就不明显，因此尾部效应也就不明显;由图5可以看出:E=0.001 eV时，其尾部效应的最大值为8.067 a20;能量为0.0075 eV时，其尾部效应为0.66 a20.

图5 He-Li2体系在不同碰撞能量时的分波截面

细看还会发现，当入射能量为0.001 eV时，其分波截面在J=4时开始收敛;入射能量为0.0075 eV时，其分波截面在J=13时开始收敛;入射能量为0.02 eV时，其分波截面在J=22时开始收敛.由此可见随着入射能量的增加，微分截面收敛所需的总角动量量子数也随之增加.对于这种现象，可以从粒子波的观点出发进行解释，中心力场势散射的半经典公式为:L≤kα(L表示粒子的轨道角动量量子数，k表示德布罗意粒子波的波数，α表示中心力场的有效作用半径)，其中k=，则得L≤α，由于在本文计算的是He-Li2体系处于基态时的转动激发，因此jα=0，则J=Lα，可以得出J≤α，由得出的这个公式可以看出:对于同一个入射粒子而言，由于质量相同，又是一个常数，所以收敛所需要总角动量量子数J正比于入射原子能量的开方，这就不难理解为什么当入射能量为0.001 eV时其收敛所需的总角动量量子数就少，仅仅有4个;而入射能量为0.02 eV时其收敛所需的总角动量量子数就多，则为22个.

由以上讨论可以得出结论:对于原子与分子的碰撞体系，分子内部的键长对分子与原子之间的相互作用势的影响是不能忽略的;对于He-Li2碰撞体系，总散射截面随入射原子能量的增大散射概率逐渐减小，微分截面的小角散射占主要部分，分波截面收敛所需总角动量量子数随入射能量的增加而增大;碰撞体系的量子效应会随入射能量的增加而减小，能量越低量子效应就越明显，尾部效应也越强.

［1］Yang X D 1991 Sci.China A 34 48(in Chinese)［杨向东1991中国科学A辑34 48］

［2］Yang X D，Wang C X，Sun G H，Jing F Q 2000 J.Sichuan University(Natural Science Edition)37 553(in Chinese)［杨向东、王彩霞、孙桂华、经福谦2000四川大学学报(自然科学版)37 553］

［3］Yang X D 1990 Sci.China A 8 833(in Chinese)［杨向东1990中国科学A辑8 833］

［4］Yang X D，Zhang J Y，Jing F Q 1998 Chin.Phys.Lett.1 14

［5］Julienne P S，Vigue 1991 Phys.Rev.A 44 4464

［6］Krotz A H，Kuo L Y，Shields T P，Barton J K 1993 J.Am. Chem.Soc.115 3877

［7］Sitlani A，Barton J K 1994 Biochemistry 33 12100

［8］Gilijamse J J，Hoekstra S，Sebastiaan Y T，Meerakker V D，Groenenboom G C，Meijer G 2006 Science 313 1617

［9］Wang R K，Linghu R F，Yang X D 2007 Acta Phys.Sin.56 2067(in Chinese)［汪荣凯、令狐荣锋、杨向东2007物理学报56 2067］

［10］Yu C R，Wang R K，Yang X D，Yin X C 2008 Acta Phys.Sin. 57 2906(in Chinese)［余春日、汪荣凯、杨向东、尹训昌2008物理学报57 2906］

［11］Fuchs M，Toennies J P 1986 J.Chem.Phys.85 7062

［12］Bodo E，Sebastianelli F，Gianturco F A，Yurtsever E，Yurtsever M 2004 J.Chem.Phys.120 9160

［13］Rubahn H G 1990 J.Chem.Phys.92 5384

［14］Rubahn H G，Bergmann K 1990 Annu.Rev.Phys.Chem.41 735

［15］Gianturco F A，Serna S，Delgado-Barrio G，Villareal P 1991 J. Chem.Phys.95 5024

［16］Marques P F，Belchior J C，Braga J P 2001 Phys.Chem. Chem.Phys.3 5521

［17］Bodo E，Gianturco F A，Yurtsever E 2006 Phys.Rev.A 73 052715

［18］Yang X D 1992 Theoretical Calculation and Program of Atomic andMolecularCollision(Chengdu:ElectronScienceand Technology University press)(in Chinese)［杨向东1992原子分子碰撞理论计算及程序(成都:电子科技大学出版社)］

［19］Shen G X，Wang R K，Linghu R F，Yang X D 2009 Acta Phys. Sin.58 3827(in Chinese)［沈光先、汪荣凯、令狐荣锋、杨向东2009物理学报58 3827］

［20］Yu C R，Wang R K，Zhang J，Yang X D 2009 Acta Phys.Sin. 58 0229(in Chinese)［余春日、汪荣凯、张杰、杨向东2009物理学报58 0229］

［21］Yu C R，Shi S H，Wang R K，Yang X D 2007 Chin.Phys.16 3345

［22］Shen G X，Linghu R F，Wang R K，Yang X D 2007 Chin. Phys.16 3352

［23］Wang R K，Shen G X，Yu C R，Yang X D 2008 Acta Phys. Sin.57 6932(in Chinese)［汪荣凯、沈光先、余春日、杨向东2008物理学报57 6932］

［24］Wang R K，Yu C R，Shen G X，Gong L X，Yang X D 2009 Acta Phys.Sin.58 3084(in Chinese)［汪荣凯、余春日、沈光先、龚伦训、杨向东2009物理学报58 3084］

［25］Wang R K，Shen G X，Yang X D 2009 Acta Phys.Sin.58 5335 (in Chinese)［汪荣凯、沈光先、杨向东2009物理学报58 5335］

［26］Zhu Z H，Yu H G 1997 Molecular Structure and Potential Energy Function(Beijing:Science press)(in Chinese)［朱正和、余华根1997分子结构与分子势能函数(北京:科学技术出版社］

［27］Linghu R F，Li J，Lü B，Xu M，Yang X D 2009 Acta Phys. Sin.58 0185(in Chinese)［令狐荣锋、李劲、吕兵、徐梅、杨向东2009物理学报58 0185］

［28］Zhang L，Zhong Z k，Zhu Z Y，Sun Y，Zhu Z H 2003 Chin.J. Chem.Phys.16 455(in Chinese)［张莉、钟正坤、朱志艳、孙颖、朱正和2003化学物理学报16 455］

PACC:3440，3450

*Project supported by the National Natural Science Foundation of China(Grant Nos.10974139，10964002)，the Doctoral Program Foundation of Institution of Higher Education of China(Grant No.20050610001)，the Governor’s foundation for Science and Education Elites of Guizhou Province(Grant No.QSZHZ2006(113))，the Science-technology Foundation of Guizhou province of China(Grant No.［2009］2066).

†Corresponding author.E-mail:xdyang@scu.edu.cn

Theoretical calculation of the low-energy scattering cross sections for He-Li2system*

Li Jin1)2)Linghu Rong-Feng1)3)Si Guan-Jie1)Yang Xiang-Dong1)†
1)(Institute of Atomic and Molecular Physics，Sichuan University，Chengdu610065，China)
2)(School of Material and Chemical Engineering，Hainan University;Hainan Provincial Key Laboratory of Research on Utilization of Si-Zr-Ti Resources，Haikou570228，China)
3)(School of Physics and Electronic Science，Guizhou Normal University，Guiyang550001，China)
(Received 10 August 2009;revised manuscript received 19 November 2009)

In this paper，the Fuchs potential model and the Close-coupling method are used to calculate the low-energy cross sections for a He-Li2scattering system.The dependences of total cross section on energies，differential section on angles，and partial wave cross section on quantum number of total angular momentum are discussed.The quantum effect on energy obtained.

close-coupling method，differential cross section，partial cross section，the Fuchs potential model

book=486,ebook=486

*国家自然科学基金(批准号:10974139，10964002)，高等学校博士学科点专项科研基金(批准号:20050610010)，贵州省优秀科技教育人才省长基金(批准号:黔省专合字(2006)113号)，贵州省科学技术基金(批准号:黔科合J字［2009］2066号)资助的课题.

†通讯联系人.E-mail:xdyang@scu.edu.cn