钪原子的自电离里德伯能级3d4s(1D2)nf2D3/2,3d4s(1D2)nf2F5/2和3d4s(1D2)np2D3/2的理论研究*
2010-09-08张新峰范士林贾凤东薛平许祥源3钟志萍
张新峰范士林贾凤东薛平许祥源3)钟志萍†
1)(教育部原子分子纳米重点实验室,清华大学物理系,北京100084)
2)(中国科学院研究生院物理科学学院,北京100049)
3)(首都师范大学物理系,北京100037)
(2009年6月15日收到;2009年12月16日收到修改稿)
钪原子的自电离里德伯能级3d4s(1D2)nf2D3/2,3d4s(1D2)nf2F5/2和3d4s(1D2)np2D3/2的理论研究*
张新峰1)范士林2)贾凤东2)薛平1)许祥源1)3)钟志萍2)†
1)(教育部原子分子纳米重点实验室,清华大学物理系,北京100084)
2)(中国科学院研究生院物理科学学院,北京100049)
3)(首都师范大学物理系,北京100037)
(2009年6月15日收到;2009年12月16日收到修改稿)
在多通道量子亏损理论框架下,利用相对论多通道理论,分别在冻结实近似和考虑偶极极化下计算钪原子的Jπ=(3/2)-,(5/2)-的三个收敛于[Ar]3d4s(1D2)的自电离里德伯系列的能级.对3d4s(1D2)np2D3/2和3d4s (1D2)nf2F5/2这两个系列,计算结果表明,考虑偶极极化效应后,理论计算和实验测量的量子数亏损之差普遍小于0.01.而对3d4s(1D2)nf2D3/2系列,考虑偶极极化效应后的结果和仅考虑冻结实的结果比较接近,理论计算和实验测量的量子数亏损之差普遍在0.04左右.
相对论多通道理论,多通道量子亏损理论,电子-电子关联,自电离里德伯系列
PACC:3120A,3120T,3280D
1. 引言
钪原子Sc的核电荷数为21,基态电子排布式为[Ar]3d4s22Do5/2,有三个价电子.Sc原子是最简单的具有未填满的子壳层的元素.由于4s轨道和3d轨道的近简并,Sc前13个电离阈的的总间隔仅为1.7 eV(14000cm-1)[1],收敛到这些阈值的里德伯系列或自电离里德伯系列的谱线密集,光谱很复杂[2].这些里德伯系列或自电离里德伯系列之间的相互作用可以展示丰富的电子-电子关联作用.因此Sc原子价电子跃迁光谱是研究电子关联效应和复杂能级结构的理想对象.同时,由于其他过渡元素和Sc类似,价电子层都含有s和d轨道[3,4],外层处于激发态的电子都具有p或者f电子,因此我们在Sc原子能级结构计算的经验也可以应用到这些元素.Sc原子在高压下还表现出超导的性质[5],能促进碳纳米结构的储氢能力[6].
在实验方面,Sc原子价电子跃迁光谱数据已经由Ralchenk.等[7]很好地总结了.关于钪的自电离里德伯能级,Garton等[8]利用拍照的方法,实验测量了钪原子处于1200—3200之间的单光子吸收谱,并识别出了八个自电离里德伯系列.Robicheaux等[3,4,9]利用脉冲染料激光激发Sc原子束探测荧光的办法,测量了能级跃迁处于4600—6000的能级跃迁,识别出更多的里德伯系列.理论方面,Robicheaux等[3,4,9]利用本征通道R-矩阵的方法计算了Garton等测量的吸收光谱,由此对Garton等[8]测量的大部分自电离系列能级重新进行了标识,其计算的能级所对应的量子数亏损和实验测量值之间的差值大部分在0.03左右.但是他们的计算方法只是近乎从头计算,即对18个核电子用带偶极偏振的屏蔽库仑势的赝势代替,通过Ls-jj表象转换引入自旋-轨道相互作用[10,11].Robicheaux等[3,4,9]在计算中共考虑了收敛于30个阈值的相关通道,大量通道的引入在取得带来较高精度的同时,也带来了巨大的计算量,对计算条件有较高要求.此外,Robicheaux等[3,4,9]的计算对大部分能级没有具体分析哪些通道对电子-电子关联效应起重要作用.最近,Jia等[12]在多通道量子亏损理论框架下,从第一性原理出发,利用相对论多通道理论对Sc原子自电离里德伯原子系列4s2nf2Fo7/2(n=4—23)作了不同层次的计算:冻结实近似,考虑偶极极化效应,考虑高阶极化效应等,从而确定哪些效应对电子-电子关联效应起主要的作用.他的计算表明,偶极极化效应非常重要.在考虑了偶极极化效应后,除n=20,22,23,计算的能级位置所对应的量子数亏损与实验测量之差为0.01—0.03.
本工作是在Jia等[12]的基础上,利用相对论多通道理论,分别在冻结实近似,以及考虑偶极极化近似的两个层次下计算了Jπ=(3/2)-,(5/2)-的三个实验数据较为完整的钪原子的自电离里德伯能级,即3d4s(1D2)nf2D3/2,3d4s(1D2)np2D3/2和3d4s(1D2)nf2F5/2三个自电离里德伯系列.
2. 理论方法
在多通道量子亏损理论(MQDT)[10,11,13—15]框架下,可以用一组物理的MQDT参数(本征量子数亏损μα、转换矩阵Uiα),对无限个里德伯态和与之相应的连续态以及自电离态做统一描述.相对论多通道量子数亏损理论(RMCT)是传统组态相互作用理论的发展,这一理论是全相对论性的和非微扰的.传统的组态相互作用方法,仅包含有限束缚组态的相互作用,因此也只能计算有限束缚态的能级和波函数.相对论性多通道理论不仅考虑了有限束缚类组态的相互作用,同时考虑了无限多的里德伯态和相应的连续态的相互作用[16—21].在此理论框架下可以计算有限束缚态的能级和波函数,束缚能域和连续能域的多通道量子亏损理论的物理参数(本征量子数亏损μα、转换矩阵Uiα).然后在MQDT理论框架下计算原子的能级位置、朗道g因子以及耦合方式.
下边我们简单介绍一下相对论多通道量子数亏损理论.
根据量子电动力学,在库仑规范下,忽略Breit相互作用和其他高阶QED[22—24]修正,可得到原子中电子所满足的狄拉克方程.为了求解多电子原子体系的狄拉克方程,可以把哈密顿量H分成两部分,即(没有特别说明,均为原子单位)

其中

为相对论性自洽场原子哈密顿量;
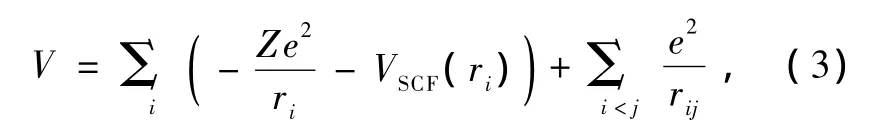
定义它为残余相互作用[23,24].
根据Dirac-Slater自洽场方法(局域交换近似),可以得到原子的相对论性自洽势VSCF.在此基础上可求出所有束缚和连续的单电子波函数a,其中a对于束缚和连续波函数分别代表量子数nk和εk.以这组单电子正交完备基函数a,在一定的电子排布下,经过反对称化以及适当的角动量耦合,就可构造出组态波函数Φn及Φjε,形成N电子体系的正交完备基函数.它们满足下式:

任意一个能量本征态波函数Ψ(E,i)可表示成

下标j表示各电离通道,所谓电离通道是指由一系列的组态波函数,具有特定的总角动量和宇称以及角动量耦合方式,其原子实处于特定状态,而激发电子轨道能量不同.能量下限c是该通道的里德伯态与作为通道处理的连续化高里德伯态的分界能量;能量积分可在适当的能量格点上进行.上式中第一项是对较低激发态的展开,第二项是对各电离通道的求和及通道内连续化高里德伯态和连续态求积分.
这样Dirac方程可以写为Lippmann-Schwinger积分方程
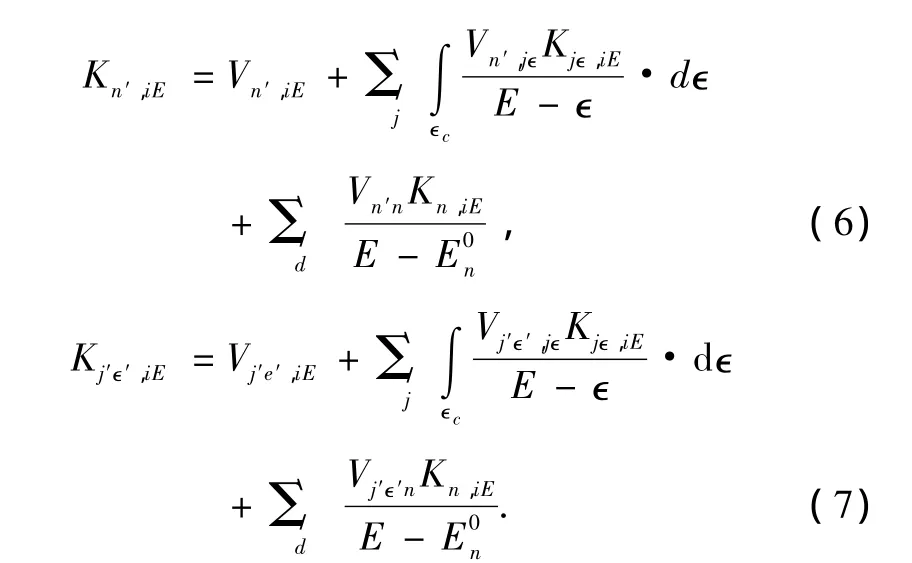
这里Vab=〈Φa|V|Φb〉,其中a,b分别代表任意两个不同的本征态.其中,微扰势Vv,v′,V,V分别代表分立-分立态,分立-连续态和连续-连续态相互作用矩阵元.
通过解积分方程,并利用对角化能壳K矩阵的方法,直接得到相对论多通道理论的物理参数(量子数亏损μα,转换矩阵Uiα).从它们出发,就可对高里德伯态,自电离态及连续态作统一处理,从而计算电子的能级结构.激发态的能量i与本征通道量子数亏损和有效量子数具有以下关系:
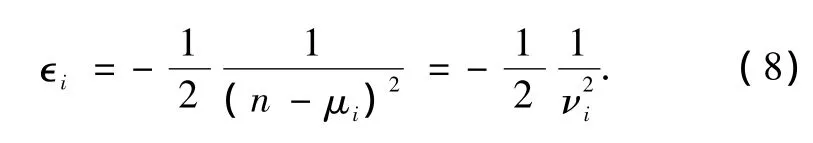
在自电离能域,μα和Uiα具有如下的关系:
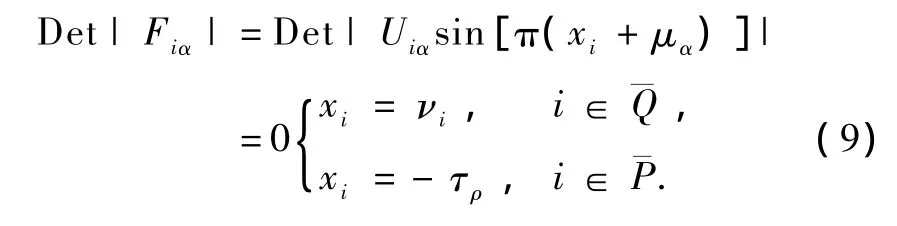
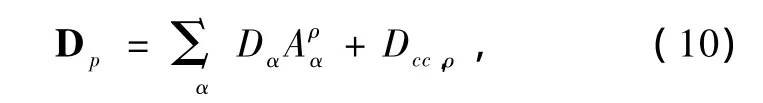
其中Dα是激发通道的偶极矩阵元,Dcc,ρ是核激发的矩阵元.Aρα是函数μα和Uiα的混合系数.
如果光谱远离核激发能区(我们所研究的能区就是远离核激发),这时从初态到第ρ个自电离通道的约化偶极矩阵元近似为
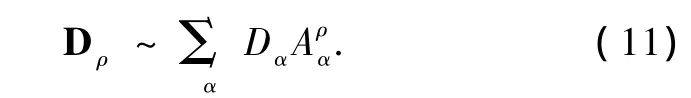
散射截面部分可以写成

其中df/dε是振子强度密度,α是精细结构常数,ω是原子单位下的光子能量.
计算中,我们关注的是哪些组态对研究能级的电子-电子关联效应起主要的作用.我们计算分为了两个层次:冻结实近似和考虑偶极极化效应.所谓冻结实近似是指忽略了由于离子实的变化而导致的电子-电子关联效应,例如对钪原子,对收敛于[Ar]3d4s1D的里德伯系列,冻结实近似认为离子实3d4s1D不受激发电子的影响,计算中只考虑收敛到3d4s1D的有关组态.实际上,必须考虑激发电子对离子实的影响,比较重要的有动态极化效应[17,18].动态极化效应是指激发电子绕核运动产生的电场使得离子实极化,导致离子实角动量变化同时为保持原子总角动量和宇称不变,激发电子状态发生相应变化.其中有|Δl|=1,2,…,这里l是离子实的角动量量子数,|Δl|=1称为偶极极化,|Δl|= 2成为四极极化,依次类推.一般来说偶极极化作用会比较大.对钪原子,离子实|Ar|3d4s,|Δl|=1对应的离子实有3d4p,3d5p,…,|Δl|=2对应3d2,4s2,….表1列出了能级[Ar]3d4s1D附近的Sc+能级结构实验值.注意从表1可以看到,对3d4s(1D2) nl能级,偶极极化效应对应的3d4p n′l′通道的能级比3d4s(1D2)nl的能级高,甚至比高阶极化效应|Δl|=2对应3d2n″l″,4s2nl通道能级都高.但我们计算4s2nf的经验表明[8],即使偶极极化效应对应的能级远远高于高阶极化效应对应的能级,但偶极极化效应对电子-电子关联作用贡献更大.因此本文只考虑了冻结实近似和考虑偶极极化效应两个层次的计算.
对于自电离谱峰的标识,在理论上是确定哪个本征通道对该自电离谱峰起主要作用.一般地,如果感兴趣的自电离谱所跨的能区比较小,我们可以认为偶极跃迁矩阵元是常数.可以令Dα′=δαα′,从而计算出特定的本征通道谱,如图1所示.通过对比实验谱和计算得到的本征通道谱,可以确定自电离峰的标识.具体说如果实验谱峰和计算的本征通道谱的峰的位置比较接近,就可以把实验峰标识为属于这个本征通道.但是本征通道谱不能准确的反映某个自电离峰的峰形,尤其是对于那些被强烈干扰的共振态.事实上,准确描述自电离谱峰的峰形可以用只考虑一个共振态和一个连续通道相互作用的Fano线形[22—24],或反映多个共振态和多个连续通道相互作用的Shore参数描述[25,26].但在通常情况下,我们这样的标识方法可以满足标识自电离谱峰的目的[27—29].注意由于组态相互作用,一个本征通道谱中可能出现两个或多个自电离里德伯系列,见图1(a)和(b).将强的里德伯系列即展开系数比较大的系列归属为该本征通道.
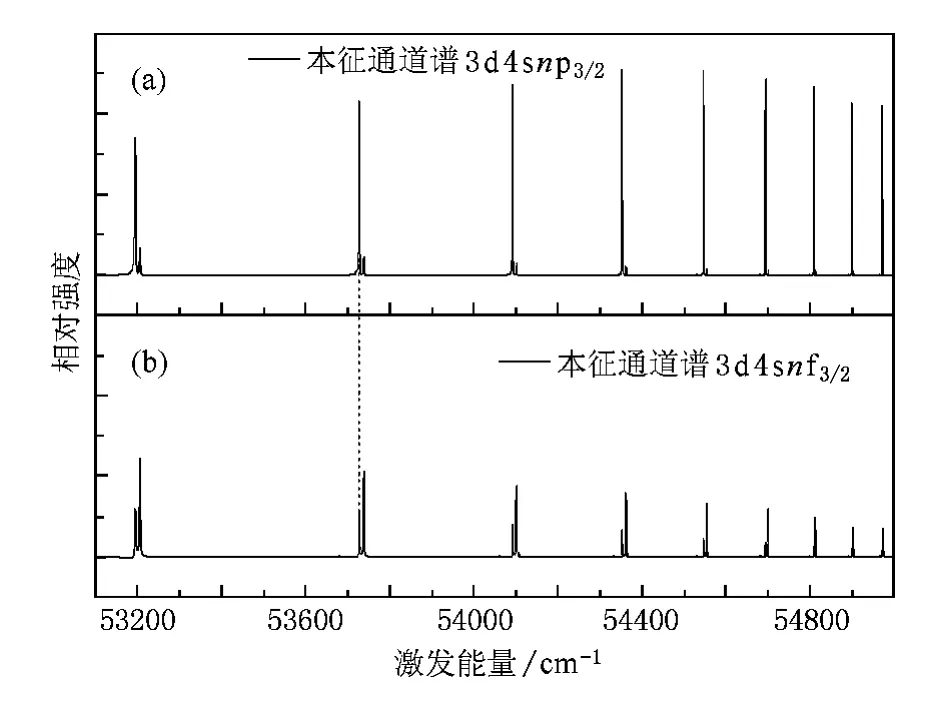
图1 计算得本征通道谱(a)本征通道谱3d4s(1D2)nf2D3/2; (b)本征通道谱3d4s(1D2)np2D3/2
关于自电离峰的峰值的确定,众所周知,在共振态能级附近,碰撞本征相移πτρ会突然改变π相位.一般在相位跳变最大处对应的跃迁截面最大,对应为该共振态的峰值,当然这只是一种粗略确定峰位的办法.
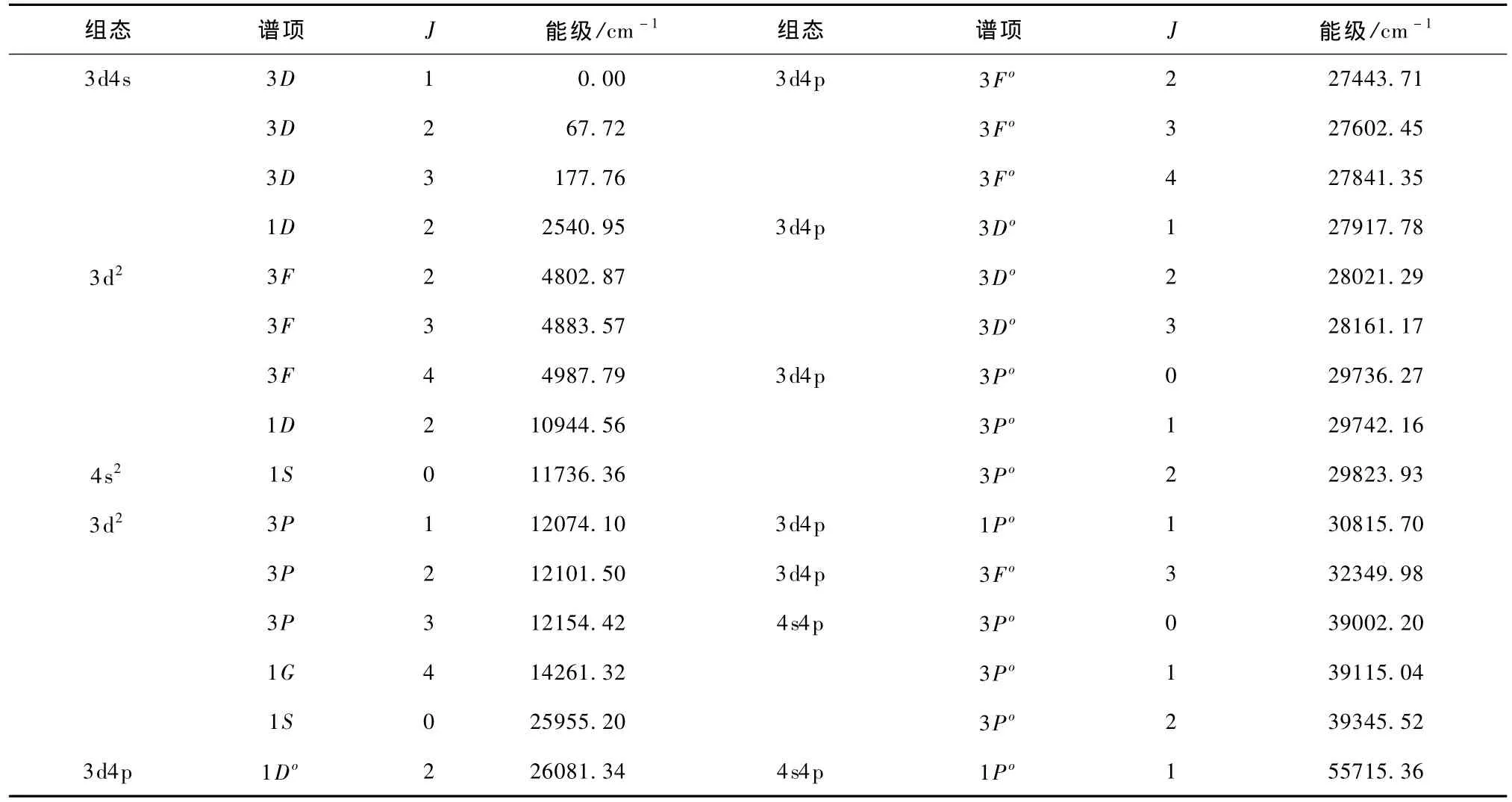
表1 Sc+能级结构实验值
3. 结果和讨论
在多通道量子亏损理论框架下,利用相对论多通道理论,分别在冻结实近似和考虑偶极极化效应下,计算了实验数据较为完整,Jπ=(3/2)-,(5/ 2)-的三个收敛于3d4s(1D2)的自电离里德伯系列(分别称为为系列1,2和3).表2至表4分别给出了钪原子自电离里德伯能级3d4s(1D2)np2D3/2,3d4s(1D2)nf2D3/2,3d4s(1D2)nf2F5/2,的计算结果以及与实验值的比较.如前所述,Robicheaux等[3,4,7]对Garton等测量的大部分自电离系列能级重新进行了整理和标识,由于他们计算的量子数亏损和实验能级量子数亏损之差大多在0.03以下,而且计算的谱形和实验所得到的谱形比较符合.因此我们采用Robicheaux等[3,4,7]整理后的实验能级系列,但组态的标识可能不同,主要是因为计算中包含的组态数不同.注意Robicheaux等[3,4,7]计算是通过LS-jj表象转换引入自旋-轨道相互作用法,给出的能级标识是LS耦合的,而我们是相对论性的计算,给出的是jj耦合的标识.
关于三个系列的标识,系列1,2我们给出的组态的标识和Robicheaux等[3,4,7]正好对调.对于系列1(表2)的实验能级,Robicheaux等[3,4,7]的标识是3d4s(1D2)nf2D3/2,我们把这个系列标识为3d4s (1D2)np2D3/2.对系列2(表3)Robincheaux等[3,4,7]标识为3d4s(1D2)np2D3/2,而我们的标识是3d4s (1D2)nf2D3/2.这个差异的原因可见图1.图1(a)和(b)是计算的3d4s(1D2)nf2D3/2和3d4s(1D2)np2D3/2两个本征通道谱.可以看出,这两个本征通道谱都出现了3d4s(1D2)nf2D3/2和3d4s(1D2)np2D3/2这两个自电离里德伯系列,这是由于组态相互作用引起.这两个里德伯系列正是表2,3研究的能级.它们出现在在一个同本征通道谱中,说明这两个里德伯系列相互作用比较强.同时由于计算中采用的组态数不同等原因,展开系数可能有差别,因此我们和Robincheaux等[3,4,7]标识不同,这是可以理解的.对系列3,我们的和Robicheaux等[3,4,7]是相同的,都是3d4s(1D2)nf2F5/2.
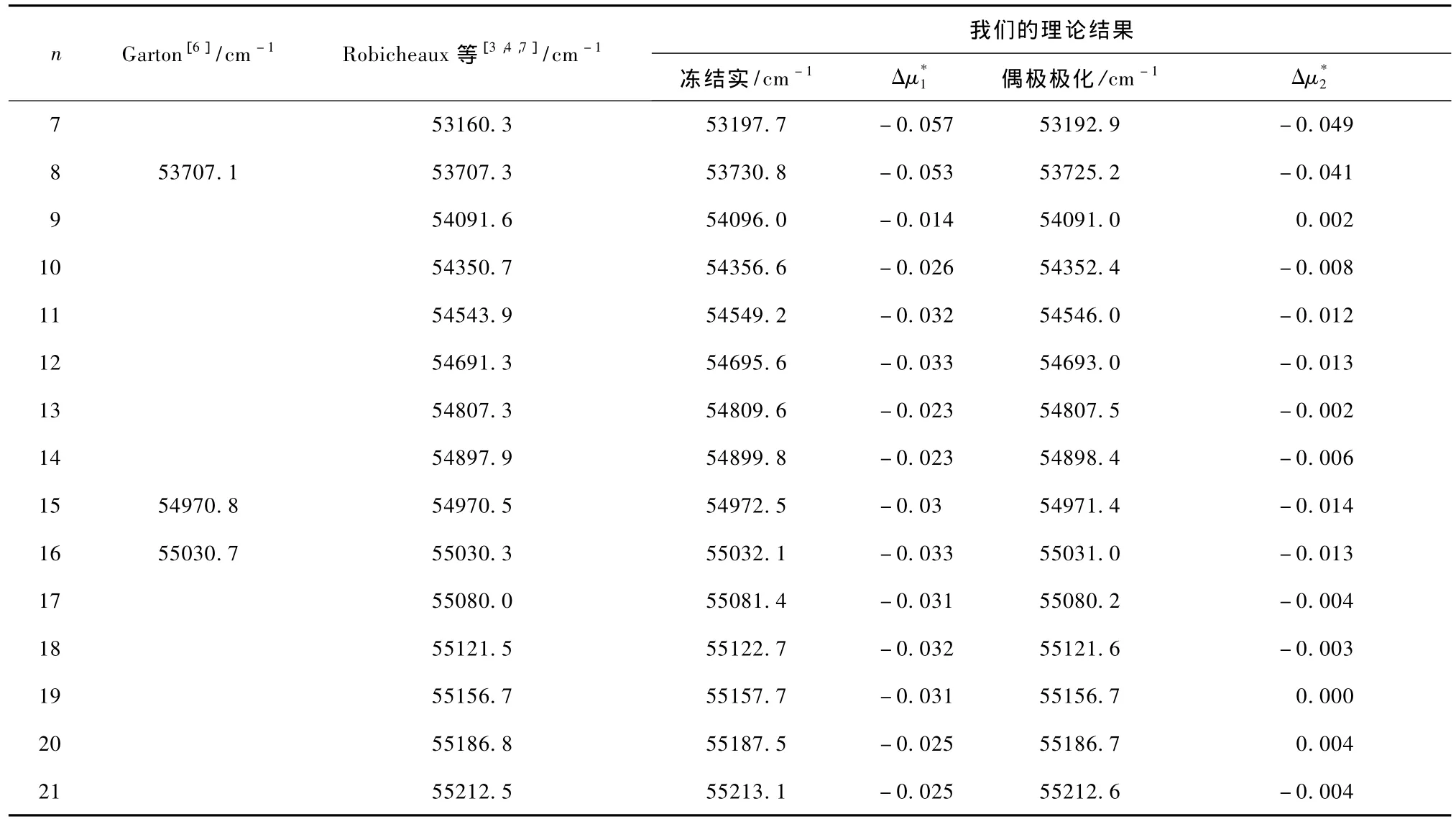
表2 系列1的理论和数据比较.我们的标识为3d4s(1D2)np2D3/2,Robicheaux等[3,4,8]标识为3d4s(1D2)nf2D3/2
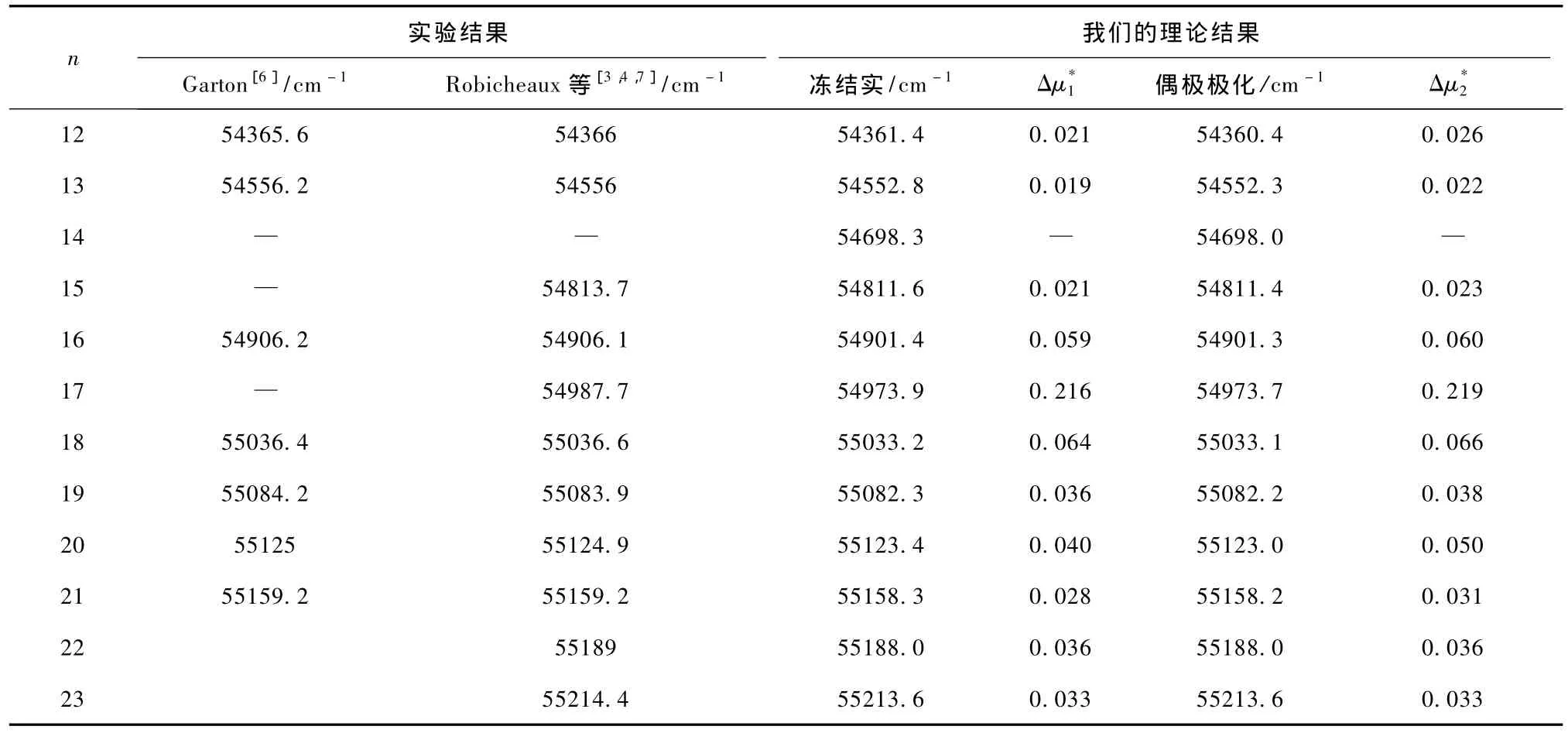
表3 系列2的理论和数据比较.我们的标识为3d4s(1D2)nf2D3/2,Robicheaux等[3,4,8]标识为3d4s(1D2)np2D3/2
下面我们讨论计算的量子数亏损与实验的差异原因.我们先分析表2和表4的结果,它们的规律比较类似:从表2(系列1,3d4s(1D2)np2D3/2)可以看出,冻结实近似的计算与实验得到的量子数亏损之差均为负,在0.06左右.对表4(系列3,3d4s (1D2)nf2F5/2)在冻结实近似下的量子数亏损之差也均为负,在0.06—0.07之间.即计算能级能量比实验值高,这个物理原因可以用二级微扰修正的图像说明:有能级较高的组态与研究能级相互作用未考虑,如果考虑进来,则将使能级低的能级降低,能级高的能级增加.事实上,在考虑偶极极化效应后,对表2(系列1,3d4s(1D2)np2D3/2)除n=7,8外,其余能级对应量子数亏损差值有正有负,在0.002—0.01之间.对表4(系列3,3d4s(1D2)nf2F5/2)也从原来的全为负值,改善到有正有负,在0.01左右.这说明对于系列1(3d4s(1D2)np2D3/2)和系列3(3d4s (1D2)nf2F5/2),偶极极化效应比较重要.且只要考虑偶极极化效应,计算的精度已经很高,与该系列能级较为接近的高阶极化效应通道对该系列能级影响可以忽略.
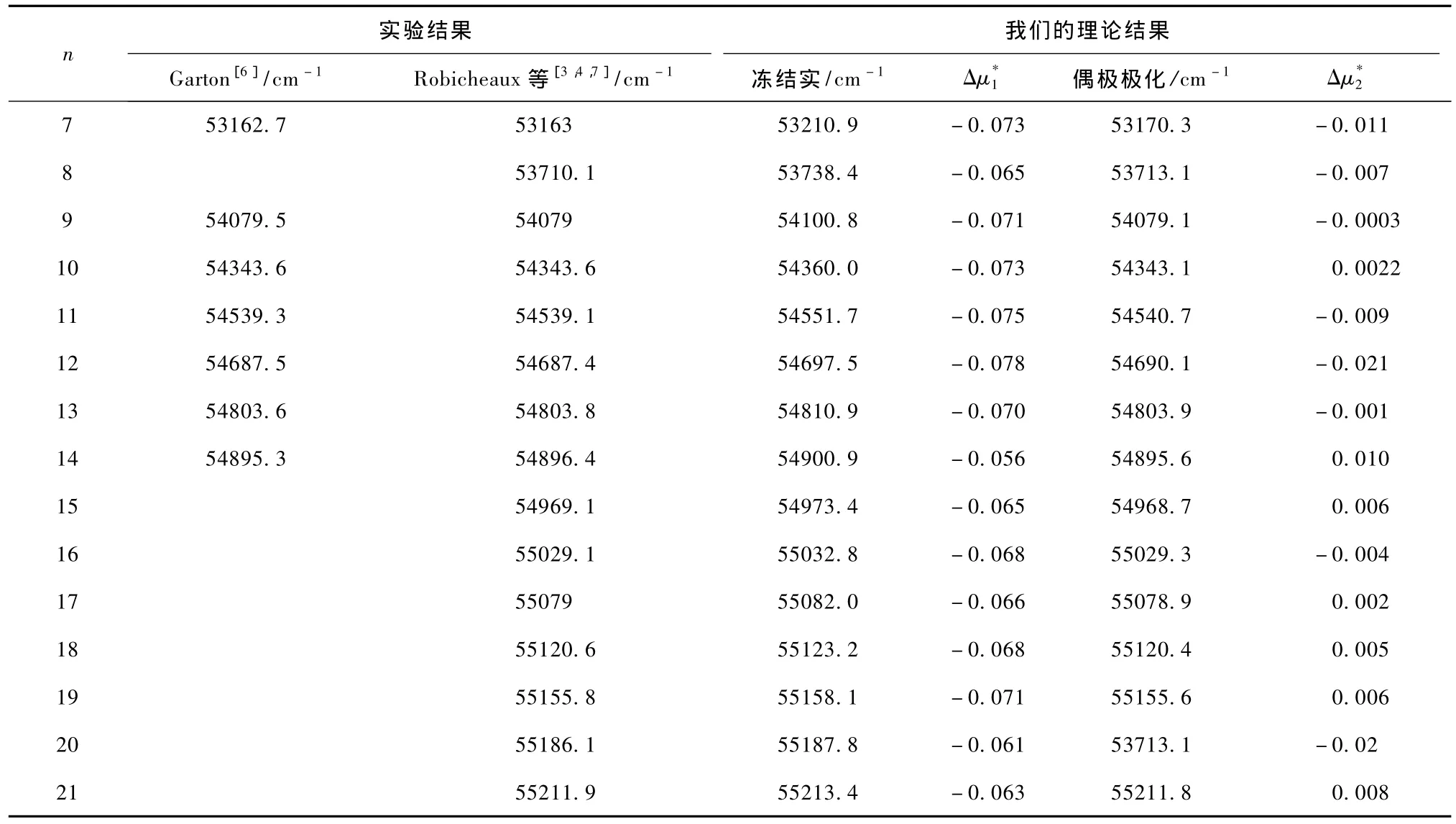
表4 系列3的理论和数据比较.我们的标识为3d4s(1D2)nf2F5/2,同Robicheaux等[3,4,8]的相同
而从表3(系列2,3d4s(1D2)nf2D3/2)的结果,可以看到,理论计算的量子数亏损和实验得到的量子数亏损之差,对冻结实和考虑偶极极化效应的基本一样.除n=17外,这个差值均在0.02—0.07之间.而n=17的能级,理论和实验的量子数亏损之差高达0.2,这有可能是由于与n=17邻近的与高阶极化效应有关的能级与之相互作用导致的.这个系列考虑偶极极化效应后,计算结果并没有如表2和表4所示的两个系列那样有明显改善,原因可能是:虽然钪原子有三个价电子,且前13个电离阈密集,使得其在第一电离阈值附近的光谱非常复杂,但是我们组以前的工作[8]和本文的结果均表明:仅考虑冻结实近似,理论计算的量子数亏损和实验值得到的量子数亏损之差一般已经小于0.1,足以满足对实验谱峰的标识.而文献[27]没有考虑偶极极化效应,只考虑冻结实近似和高阶极化效应,重构了52625—54046cm-1的复杂光谱,和实验谱符合较好,计算的量子数亏损和实验值之差也普遍小于0.1.虽然一般而言偶极极化效应比高阶极化效应重要,这一点,文献[8]的结果就是一个典型的例子.但是,若与所研究的能级邻近的是与高阶极化效应有关的能级,而与偶极极化效应有关的能级远离所研究能级,根据微扰理论,对这所研究的能级,高阶极化效应可能比偶极极化效应更重要.事实上,本文研究的能区,与偶极极化效应有关的能级位置远远高于我们研究的能区,而与高阶极化效应有关的能级却镶嵌在我们所研究的能区中.一旦与高阶极化效应有关的能级位置接近我们所研究的能级,如表3系列2 3d4s(1D2)nf2D3/2n=17,则它们之间的组态相互作用会比较显著,高阶极化效应可能比偶极极化效应更显著.这样对不同的系列,偶极极化效应和高阶极化效应的重要性可能不同.如本文研究的系列1 3d4s(1D2)np2D3/2和系列3 3d4s(1D2) nf2F5/2,考虑偶极极化效应后,计算精度大为提高,理论计算的量子数亏损和实验得到的量子数亏损之差普遍小于0.01;而系列2 3d4s(1D2)nf2D3/2考虑偶极极化效应的结果和冻结实近似结果比较接近,理论计算的量子数亏损和实验得到的量子数亏损之差普遍在0.02—0.07之间.对该系列,应该进一步考虑高阶极化效应,并标示与n=17有强组态相互作用的能级,这是我们下一步工作.
4. 结论
在多通道量子亏损理论框架下,利用相对论多通道理论,分别在了冻结实近似和考虑偶极极化效应下计算了钪原子的Jπ=(3/2)-,(5/2)-的三个收敛于[Ar]3d4s(1D2)的自电离里德伯系列的能级.对于3d4s(1D2)np2D3/2和3d4s(1D2)nf2F5/2这两个系列,偶极极化效应明显.其中系列1 3d4s (1D2)np2D3/2(见表2),考虑偶极极化效应的理论计算的量子数亏损和实验得到的量子数亏损之差从冻结实的0.03改善到0.01左右.系列3 3d4s (1D2)nf2F5/2(见表4),从冻结实近似的0.07改善到0.01.但系列2 3d4s(1D2)nf2D3/2(见表3),考虑偶极极化效应的结果和冻结实结果比较接近.理论计算的量子数亏损和实验得到的量子数亏损之差普遍在0.04左右,偶极极化效应不明显.这可能是由于与高阶极化效应有关的能级与该系列n=17的能级接近,必须考虑高阶极化效应.
[1]Kaufman V,Sugar J 1988 J.Phys.Chem.Ref.Data 17 1679
[2]Russell H N,Ward J F 1927 Scient.Pap.U.S.Bur.Stand. 22 329
[3]Robicheaux F,Greene C H 1993 Phys.Rev.A 48 4429
[4]Robicheaux F,Greene C H 1993 Phys.Rev.A 48 4441
[5]Lane W N,Papaconstantopoulos D A,Michael J M 2007 Phys. Rev.B 76 134512
[6]Durgun E,Ciraci S,Yildirim T Phys.Rev.B 77 085405
[7]Ralchenko Y,Kramida A E,Reader J,NIST ASD Team http:// physics.nist.gov/asd3[2008,December 20].
[8]Garton W R S,Reeves E M,Tomkins F S,B Ercoli 1973 Proc. R.Soc.London.Ser.A 333 1
[9]Robicheaux F,Greene C H 1993 Phys.Rev.A 48 4450
[10]Lee C M(Li J M),Johnson W R 1980 Phys.Rev.A 22 979
[11]Lee C M,Lu K T 1973 Phys.Rev.A 8 1241
[12]Jia F D,Wang J Y,Zhong Z P 2008 Chin.Phys.B 17 2027
[13]Seaton M J 1983 Rep.Prog.Phys.46 167
[14]Li J M 1980 Acta Phys.Sin.29 419(in Chinese)[李家明1980物理学报29 419]
[15]Li J M 1983 Acta Phys.Sin.32 84(in Chinese)[李家明1983物理学报32 84]
[16]Zou Y,Tong X M,Li J M 1995 Acta Phys.Sin.44 50(in Chinese)[邹宇、仝晓民、李家明1995物理学报44 50]
[17]Huang W,Zou Y,Tong X M,Li J M 1995 Phys.Rev.A 52 2770
[18]Li J M,Wu Y J,Pratt R H 1989 Phys.Rev.A 40 3036
[19]Yan J,Zhang P H,Tong X M,Li J M 1996 Acta Phys.Sin.45 1978(in Chinese)[颜君、张培鸿、仝晓民、李家明1996物理学报45 1978]
[20]Xia D,Li J M 2001 Chin.Phys.Lett.18 1334
[21]Xia D,Zhang S Z,Peng Y L,Li J M 2003 Chin.Phys.Lett. 20 56
[22]Sossah A M,Zhou H L,Manson S T 2008 Phys.Rev.A 78 053405
[23]Shi Y L,Dong C Z Acta Phys.Sin.2009 58 2350(in Chinese)[师应龙、董晨钟2009物理学报58 2350]
[24]Libermann D A,Comer D T,Waber J T 1971 Comp.Phys. Commun.2 107
[25]Li J M,Zhao Z X 1981 Acta Phys.Sin.30 105(in Chinese)[李家明、赵中新1981物理学报30 105]
[26]Fano U 1961 Phys.Rev.124 1866
[27]Fano U,Cooper J W 1965 Phys.Rev.137 A1364
[28]Ma Y P,He L M,Zhang M,Zhu Y X 2009 Acta Phys.Sin.58 7621(in Chinese)[马怡培、贺黎明、张孟、朱云霞2009物理学报58 7621]
[29]Qin W J,Dai C J,Zhao H Y,Xiao Y 2009 Acta Phys.Sin.58 209(in Chinese)[秦文杰、戴长建、赵洪英、肖颖2009物理学报58 209]
[30]Shore B W 1968 Phys.Rev.171 43
[31]Mies F H 1968 Phys.Rev.175 164
[32]Wang J Y,Zhong Z P,Jia F D,Qu Y Z,Zhong Y P 2008 J. Phys.B 11 085002
[33]Jia F D,Zhong Z P,Sun W,Xue P,Xu X Y 2009 Phys.Rev. A 79 032505
PACC:3120A,3120T,3280D
*Project supported by the National Natural Science Foundation of China(Grant Nos.10574162 and 10676014).
†Corresponding author.E-mail:zpzhong@gucas.ac.cn
Theoretical study of autoionization Rydberg series 3d4s(1D2)nf2D3/2,3d4s(1D2)nf2F5/2and 3d4s(1D2)np2D3/2of Sc*
Zhang Xin-Feng1)Fan Shi-Lin2)Jia Feng-Dong2)Xue Ping1)Xu Xiang-Yuan1)3)Zhong Zhi-Ping2)†
1)(Department of Physics,The Key Laboratory of Atomic and Molecular Nanosciences of the Ministry of Education,Tsinghua University,Beijing100084,China)
2)(Collage of Physics,Graduate University of Chinese Academy of Sciences,Beijing100049,China)
3)(Department of Physics,Capital Normal University,Beijing100037,China)
(Received 15 June 2009;revised manuscript received 16 December 2009)
In the frame work of multi-channel quantum defect theory,the energy levels of three autoionization Rydberg series converging to Sc+[Ar]3d4s(1D2)with Jπ=(3/2)-,(5/2)-are calculated from first principles by relativistic multichannel theory at two levels of approximation,i.e.,frozen core approximation and that with consideration of dipole polarization.Considering dipole polarization effect,the difference between calculated and experimental quantum defects for the 3d4s(1D2)np2D3/2and 3d4s(1D2)nf2F5/2series are smaller than 0.01,thus the dipole polarization effects are important for the two autoionization Rydberg series.While for 3d4s(1D2)nf2D3/2series,the calculated data by frozen core approximation are close to those by considering dipole polarization effects,and the difference between calculated and experimental quantum defects are generally about 0.04.
relativisticmultichanneltheory,multichannelquantumdefecttheory,electron-electroncorrelations,autoionization Rdberg series
book=590,ebook=590
*国家自然科学基金(批准号:10574162,10676014)资助的课题.
†通讯联系人.E-mail:zpzhong@gucas.ac.cn
