类钠Ni17+离子双电子复合过程理论研究*

李传莹刘晓菊孟广为王建国

1)(北京应用物理与计算数学研究所，北京100088)

2)(中国科学院等离子体物理研究所，合肥230031)

(2009年9月28日收到;2009年12月16日收到修改稿)

类钠Ni17+离子双电子复合过程理论研究*

李传莹1)†刘晓菊2)孟广为1)王建国1)

1)(北京应用物理与计算数学研究所，北京100088)

2)(中国科学院等离子体物理研究所，合肥230031)

(2009年9月28日收到;2009年12月16日收到修改稿)

使用基于相对论多组态方法的FAC程序，研究了类钠Ni17+(3s)离子通过双激发态Ni16+(3pnl，3dnl)(Δn=0激发)的双电子复合过程，得到了态选择的双电子复合截面和速率系数，并与文献中的实验和理论数据进行了对比.结果发现，计算通过3p3/210l和3p1/211l共振态的双电子复合积分截面在实验误差范围内与实验测量很好地符合，并好于全相对论的多体微扰理论计算结果.结合量子亏损理论，发现包含高里德伯态的共振双激发态的辐射跃迁和自电离速率具有较好的标度关系，利用该关系给出了近激发阈值的所有共振态的双电子复合积分截面和速率系数.比较3pnl和3dnl两个系列，发现在低温(大约小于100 eV)等离子体情况下前者速率系数比后者大，更高的温度后者大.

双电子复合过程，FAC程序，量子亏损理论，速率系数

PACC:3120A，3120T，3400，3485D

1. 引言

双电子复合过程是高温等离子体中影响等离子体电离平衡以及光谱特性的一种重要原子物理过程，其发射的双电子伴线光谱也是等离子体物理温度密度诊断的一种重要手段.双电子复合原子过程参数在惯性约束聚变(ICF)、磁约束聚变和天体物理中都具有重要应用.同时由于涉及复杂的双电子激发态，电子关联效应将对原子结构和动力学过程有重要影响，因此这也是研究原子物理多体效应的一个标准物理过程.目前兰州重离子储存环、上海电子束离子阱(EBIT)装置都可以对该过程进行细致的实验测量.

过去的实验和理论工作主要集中在入射电子能量较高的双电子复合过程，这些过程涉及的双激发态与基态的主量子数相差1以上(Δn≥1).随着高精度的储存环合并束技术的发展，近年来有大量工作测量低能的双电子复合过程，涉及的双激发态靠近电离阈值，两个电子中一个电子的主量子数与基态相同(Δn=0)，另一个电子处在高里德伯态，如类锂离子Ar15+［1］，N4+［2］和F6+［3］等的双电子复合过程.对于这些靠近电离阈值的双激发态，Auger电子的能量接近零值，准确计算电子双激发态的能量和自电离速率是对理论研究的一个重要挑战.特别是电子关联、相对论效应等都会对理论计算结果的准确性有很大影响.最近，Fogle等［4］利用储存环上的合并束技术测量了类钠Ni17+离子的双电子复合过程

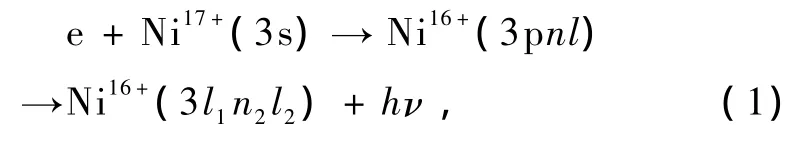
给出了自由电子能量低于6.5 eV的双电子复合积分截面和速率系数.类Na体系比类Li体系更为复杂，要准确给出双电子复合过程的共振位置和积分截面更为困难，尤其是对于激发电子Δn=0的跃迁过程.Fogle等［4］利用相对论多体微扰的方法对该过程进行了计算，但一些积分截面，如3p3/210s共振态，与实验符合得并不好.另外，理论工作只给出了实验测量的能量范围的计算结果，从应用和规律研究的角度看都应该扩展到更高的能区.因此有必要对该过程进行更深入的研究.

本文使用基于相对论多组态方法的FAC (flexible atomic code)程序［5—7］计算了类钠Ni17+(3s)离子的双电子复合过程，给出了双激发态3p1/2nl(n=11—16)和3p3/2nl(n=10—16)的能级、自电离速率、辐射跃迁速率，进一步计算了经过这些中间态的双电子复合积分截面和速率系数，并与文献［4］中的实验和理论数据进行了对比和分析.结果表明，我们的理论计算积分截面在实验误差范围内与实验测量很好地符合，总体上要比全相对论多体微扰计算的结果［4］要好.根据量子亏损理论，对于更高的里德伯态3pnl(n=17—35)，我们使用3p16l的双激发态能级、自电离速率和辐射跃迁速率进行了外推，得到了相应的积分截面和速率系数.此外，我们还计算了双激发态3d3/2nl(n= 7—12)和3d5/2nl(n=7—12)的能量、自电离速率、辐射跃迁速率、积分截面和速率系数，对于更高的里德伯态3dnl(n=13—31)，我们使用3d12l的双激发态能级、自电离速率和辐射跃迁速率进行了外推，得到了相应的积分截面和速率系数.

2. 理论方法

我们采用孤立共振近似计算双电子复合过程.在该近似下，双电子复合过程可以看作两步过程［8］，第一步:一个具有一定能量的自由电子与一个带电离子Xq+碰撞，将带电离子中一个束缚电子激发到较高激发态，同时该自由电子由于失去部分能量而被共振俘获到一个束缚态，从而形成一个共振双激发态，这个过程叫双电子共振俘获过程;第二步:共振双激发态通过自发辐射而衰变成为不能发生自电离的离子，并放出特定能量的光子，该双激发态也可以通过自电离与自发辐射过程相竞争.

2.1. 双电子复合的积分截面

双电子复合过程的第一步是双电子共振俘获过程，其逆过程是自电离过程，这一对正逆过程之间满足细致平衡关系.所以双电子俘获的截面可以由自电离速率表示出来，将双电子俘获的截面对入射电子的能量进行积分就得到双电子俘获的积分截面，即双电子俘获强度

其中me是电子的质量，gj和gi分别是双电子俘获所形成的双激发态j和初态i的统计权重，Aa(j→i)是自电离速率，Eij是共振能量.双激发态j既可以通过发射光子而衰变到较低的态d，也可以通过自电离而衰变.如果自发辐射过程的末态d的能量仍然高于电离阈值，那么它可以进一步通过自发辐射过程或者自电离过程而衰变，这样的过程叫做级联辐射过程.当考虑级联辐射时，双电子复合过程的分支比是

其中Ar是辐射速率，f和d分别代表能量低于电离阈值和高于电离阈值的态，i是自电离过程的末态.

对我们研究的双电子复合过程，由于我们计算出来的自电离速率远大于辐射速率，一般大两个量级以上，因此(3)式中的Brd很小，并且由于能级差小，辐射末态高于电离阈值的辐射速率)远远小于辐射末态低于电离阈值的辐射速率，因此对我们研究的这个体系，级联辐射过程是不重要的，本文忽略其效应，则双电子复合过程的分支比是

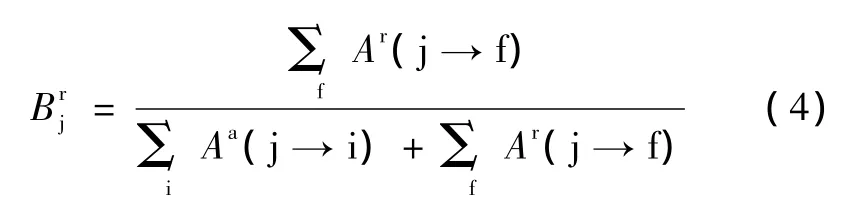
其中f代表能量低于电离阈值的态.

双电子复合过程的积分截面，即双电子复合强度可以表示为

2.2. 双电子复合的速率系数

当自由电子的速度分布是麦克斯韦速度分布时，双电子复合的速率系数为

其中Te=kT，Te是电子温度，k是玻尔兹曼常数.

在储存环的实验中，自由电子的速度分布是双温型的［9—11］，即这里v⊥和v‖分别为垂直和平行于离子束方向的电子速度分量，T⊥和T‖分别为v⊥和v‖对应的电子温度，T‖T⊥.

相应的双电子复合的速率系数为［11］

其中vd是相应于共振能量Eij的速度，vd=，v0是相应于质心能量E0的速度，du为误差函数.

3. 计算结果及讨论

利用FAC程序，我们计算了双激发态3p1/2nl(n =11－16)，3p3/2nl(n=10—16)，3d3/2nl(n= 7—12)和3d5/2nl(n=7—12)的能级、自电离速率、辐射跃迁速率，然后利用(2)—(8)式计算了Ni17+离子经过这些中间态的双电子复合积分截面和速率系数.对于更高的里德堡态3pnl(n=17—35)，根据量子亏损理论，我们对双激发态能级、自电离速率和辐射跃迁速率进行了外推，得到了相应的积分截面和速率系数.

表1给出了3p3/210l和3p1/211l的部分双激发态能量、自电离速率、辐射跃迁速率，以及Ni17+离子经过这些中间态的双电子复合积分截面，并与文献［4］中的理论数据进行了对比.需要指出的是，与文献［4］一样，我们根据NIST数据库的能级表对3p1/2－3s1/2，3p3/2－3s1/2，3d3/2－3s1/2和3d5/2－3s1/2的能级差进行了修正.这些是对双电子复合过程贡献最大的双激发态.可以看到，本文计算的双激发态能级与文献［4］的结果很好地符合，最大差别也小于1%，特别是靠近阈值的态，由于积分截面反比于共振能量，因此这些态对积分截面的贡献最大.两种方法计算的自电离速率和辐射跃迁速率大部分差别在15%以内，但由于自电离速率比辐射跃迁速率大两个量级左右，因此从(5)式可以看到，积分截面主要由辐射跃迁速率决定.我们计算的辐射跃迁速率大部分比文献［4］高约10%—20%左右，因此大部分态的积分截面也高约10%—20%左右.

表1 Ni16+离子双激发态3p1/211l和3p3/210l的部分能级、自电离速率、辐射跃迁速率，以及Ni17+离子通过这些中间态的双电子复合积分截面，并和Fogle等［4］的理论结果的比较

通过对双激发态的精细结构能级求和，我们在表2给出了Ni17+离子经过双激发态3p3/210l和3p1/211l的不同角量子数的双电子复合积分截面，并和文献［4］中的实验和理论数据进行了对比.可以看到，我们计算的积分截面在实验误差内与实验完全符合.文献［4］采用多体微扰理论计算的一些积分截面与实验符合得并不好，特别是3p3/210s共振态，主要是辐射跃迁速率的计算精度问题，或者他们采用的辐射末态不够，也可能是电子关联效应考虑的不好.在的计算中，我们不但考虑了相同主量子数组态之间的相互作用，也包含了近邻主量子数组态之间的相互作用.

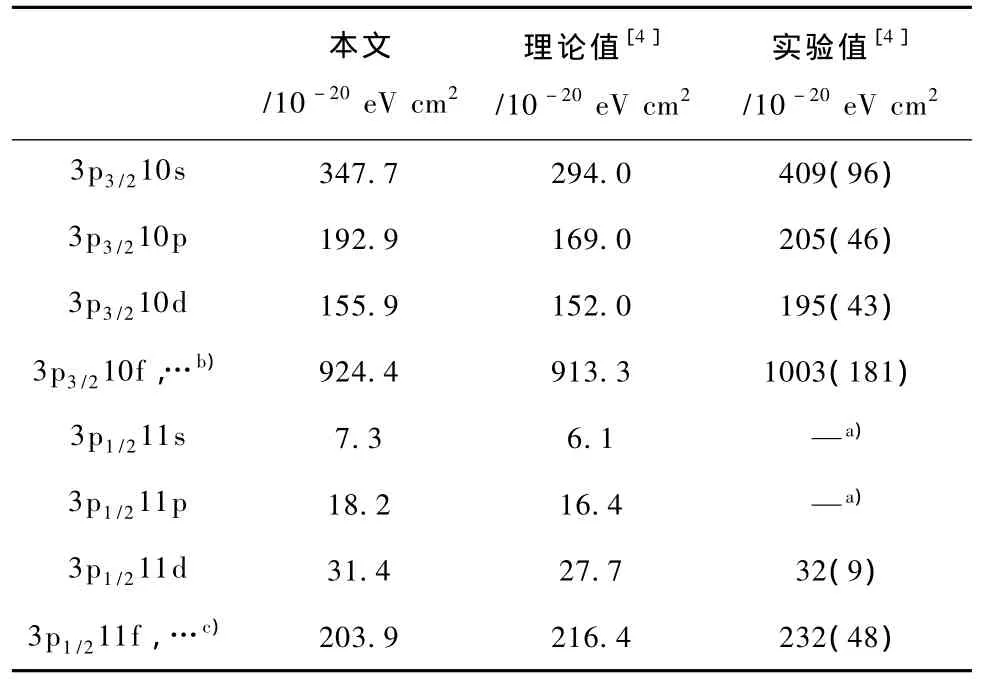
表2 Ni17+离子经过3p3/210l和3p1/211l共振态的双电子复合积分截面，并与Fogle等［4］的理论及实验结果的对比

为了与储存环的高精度实验［4］进行对比，我们计算了自由电子速度分布满足(7)式时的双电子复合速率系数.我们选kT⊥=1 meV，kT‖=0.1 meV与实验一致，计算的速率系数与文献［4］中的理论及实验结果进行了对比，如图1所示.可以看到，不论共振峰的位置还是强度与实验测量的结果都非常符合.

通过我们的理论计算和实验测量结果的对比，检验了我们的理论计算的可靠性.接着我们进一步把计算扩展到高里德堡态，更高能量的双电子复合过程.

图1 Ni17+离子的双电子复合速率系数及与其他实验和理论的对比(计算中取kT⊥=1 meV，kT‖=0.1 meV.粗黑实线是本文结果，细灰色实线是Fogle等［4］采用多体微扰理论计算的结果，具有噪声背景的灰色线是Fogle等［4］的实验结果)

根据量子亏损理论，对于更高的双激发共振里德堡态3pnl(n=17—35)或3dnl(n=13—31)，我们利用3p16l或3d12l的双激发态能级、自电离速率和辐射跃迁速率进行了外推，得到了相应的积分截面和速率系数.对能级进行外推的公式如下:

这里μl为高激发态电子的量子亏损，可以通过相邻的能级差计算得到，这里采用单通道近似［12］.

对辐射跃迁过程，当只有一个活动电子时，对自发辐射速率的外推分成两种情况:一是3pnl到3snl的跃迁过程，由于nl为高里德伯态，它对内层3p到3s跃迁过程的影响应该随着n的增加越来越小，见图2(a)，因此当n>16我们就用n=16的值来近似.由于3p12l已经是双激发态，而本文忽视级联辐射过程，所以我们对3d12l的辐射速率进行外推时不需考虑这种情况.二是外层电子从3pnl到3pn′l′或者从3dnl到3dn′l′的跃迁过程.根据量子亏损理论，辐射速率随主量子数n的增大逐渐呈现n－3标度［13］，从图2(b)可以看到n3Ar随主量子数n的增大逐渐趋向常数，因此对n>16的情况，可以用n－3标度关系进行外推.由于考虑了组态相互作用，所以计算结果中包括了辐射过程中存在两个活动电子的情况，考虑到这样过程的辐射跃迁速率很小，我们仍按照n－3标度律来外推这类辐射跃迁速率.对自电离过程，对n>16的情况，自电离速率也存在近似n－3标度关系［13］.图2(c)给出了几个计算的例子，可以看到n3Aa随着主量子数n的增大逐渐趋向常数［13］，因此我们仍然按照n－3标度律来外推自电离速率.

图3是对应于3p3/2nl(n=10—0)和3p1/2nl(n =11—20)的不同角量子数的积分截面.可以看到，积分截面不仅随着主量子数n的增加而逐渐减小，而且随着角量子数l的增加而减小.对我们计算的体系，AaAr，根据(5)式，积分截面SDijR∝Ar近似成立.由于Ar随着n的增大存在趋于常数和n－3标度变化两种情况，所以SDijR随着n的增大不一定符合n－3标度.对于本文计算的体系，当从3p16l到3s16l的辐射速率远远小于以3p16l为初始能级的其他所有辐射速率之和时，SDijR随着n的增大才基本符合n－3标度.

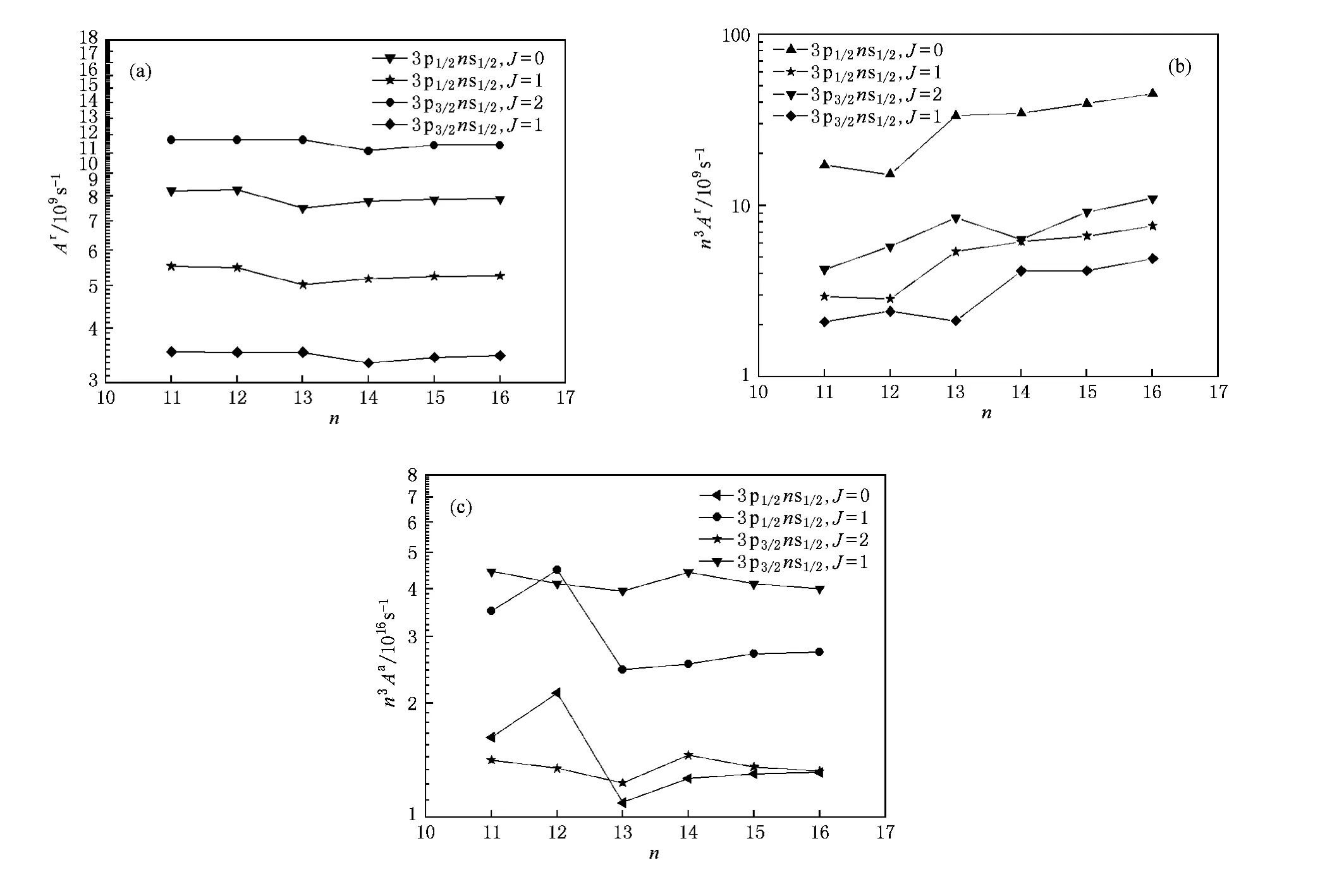
图2 Ni16+离子双激发态3p1/2，3/2ns1/2(n=11—16)四个通道中辐射速率和自电离速率随主量子数n的变化规律(a)3p1/2，3/2ns1/2(n =11—16)到3s1/2ns1/2(J=1)的辐射速率随n的变化规律;(b)3p1/2，3/2ns1/2(n=11—16)到能级3p1/23p3/2(J=1)的辐射速率随n的变化规律;(c)3p1/2，3/2ns1/2(n=11—16)的自电离速率随n的变化规律

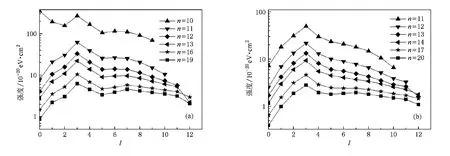
图3 Ni17+离子经过双激发态3pnl的不同角量子数l的积分截面(a)对应3p3/2nl(n=10—20)中间态;(b)对应3p1/2nl(n= 11—20)中间态

包含这些外推的高里德伯态，我们仍然采用文献［4］的实验双温分布:kT⊥=1 meV，kT‖=0.1 meV重新计算了通过双激发态3pnl(n≤35)和3dnl(n≤ 31)的双电子复合速率系数，如图4.可以看到速率系数，随着共振能量增加逐渐降低，并在较高的能区收敛于连续态.另外，对比两个共振态3pnl(n≤35)和3dnl(n≤31)的速率系数，可以发现3pnl(n≤35)有两个系列3p1/2nl(n≤35)和3p3/2nl(n≤35)，而3dnl(n≤31)只有一个系列，这是由于实验分辨率不足以分开3d3/2nl(n≤31)和3d5/2nl(n≤31).希望兰州近代物理研究所的储存环实验可以测量到Δn= 0的这几个双电子复合系列.

图4 Ni17+离子通过双激发态3pnl(n≤35)(a)和3dnl(n≤31)(b)的双电子复合速率系数(计算中取kT⊥=1 meV，kT‖=0.1 meV)

在实际的应用中，不论是天体物理或实验室环境中，等离子体的自由电子都是麦克斯韦分布的，因此我们也计算了该分布下Ni17+离子Δn=0跃迁的双电子复合速率系数，见图5.可以看到，速率系数随主量子数n的增加而逐渐减小，但并没有明显的标度关系，这是与图3中的积分截面一致的.对比3pnl和3dnl系列，可以发现当温度大约小于100 eV时，前者的速率系数大，这主要是由于前者有很多靠近阈值的共振态;而当温度约大于100 eV时，后者的速率系数大，这主要是由于后者的统计权重大.

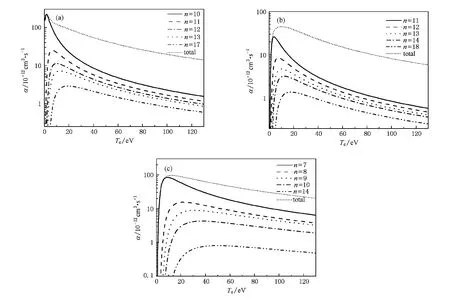
图5 利用自由电子麦克斯韦分布计算的Ni17+离子双电子复合速率系数(a)通过共振激发态3p3/2nl(n≤35);(b):通过共振激发态3p1/2nl(n≤35);(c):通过共振激发态3dnl(n≤31)

4. 结论

本文使用相对论多组态方法研究了类钠Ni17+离子Δn=0的双电子复合过程，得到了通过3pnl(n≤16)和3dnl(n≤12)各双激发态的积分截面和速率系数.靠近阈值的共振态积分截面在实验误差内与Fogle等［4］的实验很好地符合，并好于他们的多体微扰理论计算.基于量子亏损理论，我们研究了包含高里德堡态的共振双激发态的标度性质，发现辐射跃迁和自电离速率仍能保持较好的n－3标度关系，利用该标度关系我们得到了接近激发阈值的所有共振积分截面，并计算了对应的速率系数.电子数小于9的离子的Δn=0双电子复合过程，主要是离子2s到2p的激发并俘获一个自由电子，但类钠Ni17+离子不但有3s到3p的激发过程，还有3s到3d的激发，特别是我们发现后者的速率系数在电子温度约大于100 eV时，要比前者大.值得提醒的是，我们的计算并没有包含Δn=1的双电子复合过程，在较高的温度，Δn=1的双电子复合速率系数要大于Δn=0的情况，一些低共振态会进入Δn=0系列中，本文不再详细讨论.

［1］Zong W，Schuch R，Lindroth E，Gao H，DeWitt D R 1997 Phys.Rev.A 56 386

［2］Glans P，Lindroth E，Badnell N R，Eklow N，Zong W，E Justiniano，Schuch R 2001 Phys.Rev.A 64 043609

［3］Tokman M，Eklow N，Glans P，Lindroth E，Schuch R 2002 Phys.Rev.A 66 012703

［4］Fogle M，Eklow N，Lindroth E，Mohamed T，Schuch R，Tokman M 2003 J.Phys.B:At.Mol.Opt.Phys.36 2563

［5］Gu M F 2003 Astrophy.J.582 1241

［6］Gu M F 2003 Astrophy.J 589 1085

［7］Gu M F 2003 Astrophy.J 590 1131

［8］Wang J G，Zou Y，Chang T Q 1997 Acta Phys.Sin.46 11(in Chinese)［王建国、邹宇、常铁强1997物理学报46 11］

［9］Shi W，Bartsch T，Bohme C，Brandau C，Hoffknecht A，Knopp H，Schippers S 2002 Phys.Rev.A 66 22718.

［10］Andersen L H，Pan G Y，Schmidt H T 1992 Phys.Rev.A 45 7868.

［11］Kilgus G，Habs D，Schwalm D，Wolf A 1992 Phys.Rev.A 46 5730

［12］Wang J G，Tong X M，Li J M 1996 Acta Phys.Sin.45 1(in Chinese)［王建国、仝晓民、李家明1996物理学报45 1］

［13］Wang J G，Takako Kato，Izumi Murakami 1999 Phys.Rev.A 60 2104，3750

PACC:3120A，3120T，3400，3485D

*Project supported by the National Natural Science Foundation of China(Grant No.10974021).

†E-mail::li_chuanying@iapcm.ac.cn

Theoretical study of the dielectronic recombination process of Ni17+ions*

Li Chuan-Ying1)†Liu Xiao-Ju2)Meng Guang-Wei1)Wang Jian-Guo1)

1)(Institute of Applied Physics and Computational Mathematics，Beijing100088，China)

2)(Institute of Plasma Physics，Chinese Academy of Sciences，Hefei230031，China)

(Received 28 September 2009;revised manuscript received 16 December 2009)

We studied the dielectronic recombination processe of Ni17+(3s)through the resonant doubly excited states Ni16+(3pnl，3dnl)(Δn=0)using the Flexible Atomic Code(FAC)which is based on a relativistic configuration interaction method.We obtained the cross sections and the rate coefficients and compared them with the experimental data and other theoretical results.The integrated cross sections through the resonant doubly excited states 3p3/210l and 3p1/211l are in a good agreement with the measurements within the experimental errors.In combination with quantum defect theory，we have found out that the radiative rates and the auger rates of the resonant doubly excited states involving high Rydberg states obey a good scaling law，by means of which we obtained the integrated cross sections and the rate coefficients of all the resonances close to the thresholds.A comparison of the series 3pnl and 3dnl indicates that the rate coefficients of the former are larger when the temperature is below～100 eV，and are smaller when the temperature is higher.

dielectronic recombination，FAC code，quantum defect theory，rate coefficient

book=605,ebook=605

*国家自然科学基金(批准号:10974021)资助的课题.

†E-mail:li_chuanying@iapcm.ac.cn