采用BP神经网络建立咸潮入侵预报模型——以钱塘江为例

◎ 浙江大学控制科学与工程学系 杨兴果 张宏建 周洪亮

1 引言

现今成熟的三维数值模型可以用来很好的解决咸潮问题，但是工程应用中数值模型通常需要大量的数据和工作来对数值模型进行校验和检查，当影响因素发生变化时，不能快速的做出变化。而简单的一维模型或者时间序列模型在基本的工程研究中能由潮汐河流的修改快速做出盐度变化的基本估计，这一点是非常有用[1]。影响咸潮入侵的因素较多，数据量大，如何识别有意义的因素，并充分利用这些数据是模型构建中的一个重要问题。

人工神经网络在多元非线性时间序列模型的信号处理和控制中得到了广泛的应用[2]，影响咸潮入侵变化的因素主要有：潮水位、流量、杭州湾外海的盐度等，针对这些以下部分给出了输入变量的确定方法和神经网络模型预测钱塘江咸潮入侵变化的应用。因为神经网络模型相比较水利输移模型需要获得的水利数据少的多，所以它为工程使用者获得快速评估工程的潜在影响或者河流管理提供了一个很好的补充工具。

2 研究范围

钱塘江河口段以潮强流急、涌潮汹涌而著称。张潮流可一直上溯到距河口上游130km处的富阳附近，由于潮流强，钱唐江河口的盐淡水混合属垂向均匀混合型，盐水的入侵界线随钱塘江径流大小而上下移动，枯季盐水可上溯到杭州市以上，影响杭州市的工农业和生活用水。

据调查，钱塘江流域内主要县市用水量的85%来源于钱塘江，杭州市13个县市区现有集中式生活供水厂50家左右，取水量约258.43万m3/d，绝大部分取自钱塘江；同时，钱塘江还承担着发电、防洪、灌溉等功能。为此，需要预测河口盐水入侵情况，为节约用水，顶潮抗咸措施和水厂的取水口取水方案提供依据。

钱塘江研究范围内水文测站布局如图1所示。其中富春江水电站为流量控制点作为模型的上边界；乍浦水文站监测潮位、海水盐度数据作为模型的下边界。上下边界之间的有：桐庐水文站、富阳水文站、闻家堰水文站、闸口水文站、七堡水文站、仓前水文站，各水文站监测的水文数据作为模型的输入变量见表1所示。

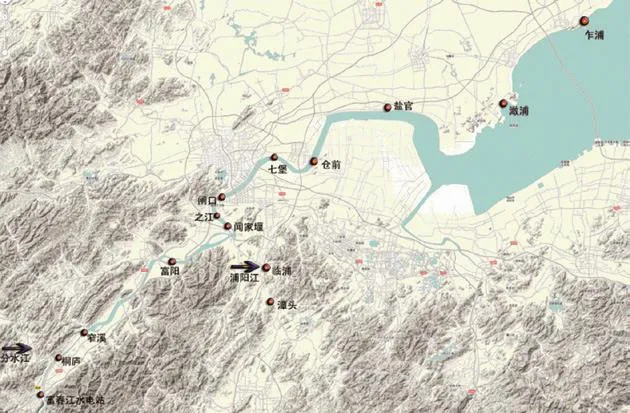
图1 研究范围内水文测站布局图

3 模型建立

杭州市现有：清泰水厂、祥符水厂、南星水厂、九溪水厂和赤山埠水厂五家。其中清泰水厂、南星水厂、九溪水厂和赤山埠水厂使用钱塘江水源，祥符水厂使用东苕溪水源。钱塘江季节性的潮汐现象，引入下游咸水影响水质。

日盐度时间序列从七堡水文站、仓前水文站、澉浦水文站获得、日流量从富春江水电站水文站、和分水江水文站获得、日潮位两个高潮位、两个低潮位数据从各个水文站获得。因为降雨量、蒸发量在收集的数据期间比较小可以忽略，这样只有富春江水电站的流量和分水江的流量作为径流输入。

本文使用BP算法训练的前馈多层感知器来进行研究。神经网络模型采用matlab编程实现。

3.1 模型输入选择

水文数据量通常很大，这些数据大多是非线性、不稳定、存在噪声。神经网络是数据驱动型模型，可以辨识输入数据间的非线性关系，但是数据间冗余性会使得神经网络输入的数据很多，网络结构复杂，计算效率降低，因此需要对输入神经网络的变量进行筛选[3]。

目前大多数研究采用“近大远小”或周期性原则通过经验来判断历史时间序列值作为输入项，因此模型输入项的确定相当随意。本文通过相关分析方法分析不同历史时刻序列值与当前时刻预测对象的相关性水平来进行选择，就使得模型输入项选择过程比较科学，有定量指标可依，对提高模型的泛化能力，降低模型输入维数，简化模型结构有很好的作用[4]。

3.1 历史数据相关性分析

X={xi, i=1,2,…, n}表示模型某一输入变量的历史时间序列，Y={yi,i=1,2,…, n}表示模型输出变量的历史时间学列。令X1={xi, i=1,2,…, n-t}, Y={yi, i=t+1,2,…, n}, 其中0≤t≤n-1，则X1和Y的标准差为：

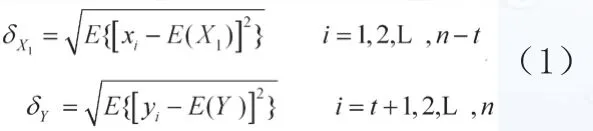
上式中，E(·)为数学期望。

X1和Y的相关系数RX1Y为：

品质得分在54.70以上的为优质一级烤鸭，市售优质烤鸭中检测到的9种杂环胺总含量水平为5 757.02～6 859.31ng·g-1。

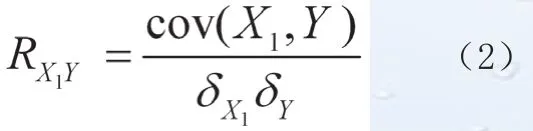
（2）式中，cov(X1, Y)为X1和Y的协方差，i=1,2,…, n-t。RX1Y表示前t时刻变量X和当前时刻变量Y之间的相关系数。X和Y相同时表示前t时刻和当前时刻同一变量的自相关系数。

3.2 主成分分析

影响咸潮的变量有很多，其中主要变量是流量、各水文站的潮水位、各水文站的盐度，由于输入变量很多，各个变量之间存在一定的相关性，全部作为输入变量输入到神经网络模型中，不仅使模型结构复杂、计算效率降低、还降低了模型的泛化能力。因此需要采用主成分分析法（PCA）提取输入变量中的主成分信息，降低输入维数。

主成分分析法的原理是相似的输入很有可能属于同一类，而输入变量方差越大，相关性越小，越有可能具有好的区分能力。主成分分析方法如下，原输入矩阵

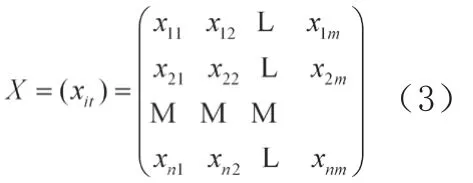
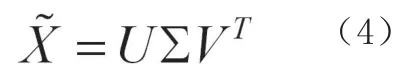
其中：Σ=diag[λ1,λ2,…,λs…,λk]式中：k为特征值个数，λ1≥λ2≥…≥λs…≥λk为对应的奇异值。实际应用时选取累计贡献率达到较高比例的前s个特征值作为神经网络模型的输入项。输入矩阵降维为：

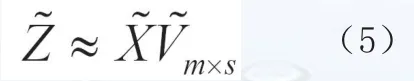
这样原始变量信息损失很小的情况下有效降低了输入项维数，并且避免了预报输入项间的相关性，可以有效的降低网络结构，提高网络的泛化能力。

4 实例分析与仿真

本文预测七堡水文站15天盐度的变化情况，模型输入数据变量见表1所示。选取13个变量的前60天历史数据分别与输出的七堡盐度数据时间序列做相关分析，确定输入变量的时间序列。对13个输入变量作相关分析得降维后的输入矩阵。（如表1）

相关系数曲线如图2所示，13个输入变量与输出变量之间的前15天相关系数的绝对值大部分都较大（＞0.5）即与输出相关性较强，因此确定输入的历史时间序列为前15天的数据。

4.2 主成分分析

经主成分分析后前7个特征值的累积贡献率达到96.495%，选取前7个因子作为模型的输入项，即输入变量由原来的13个降维为7个。

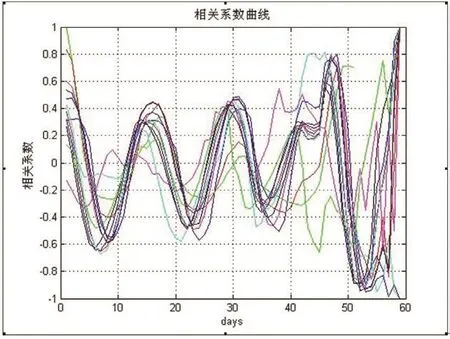
图2 相关系数曲线图

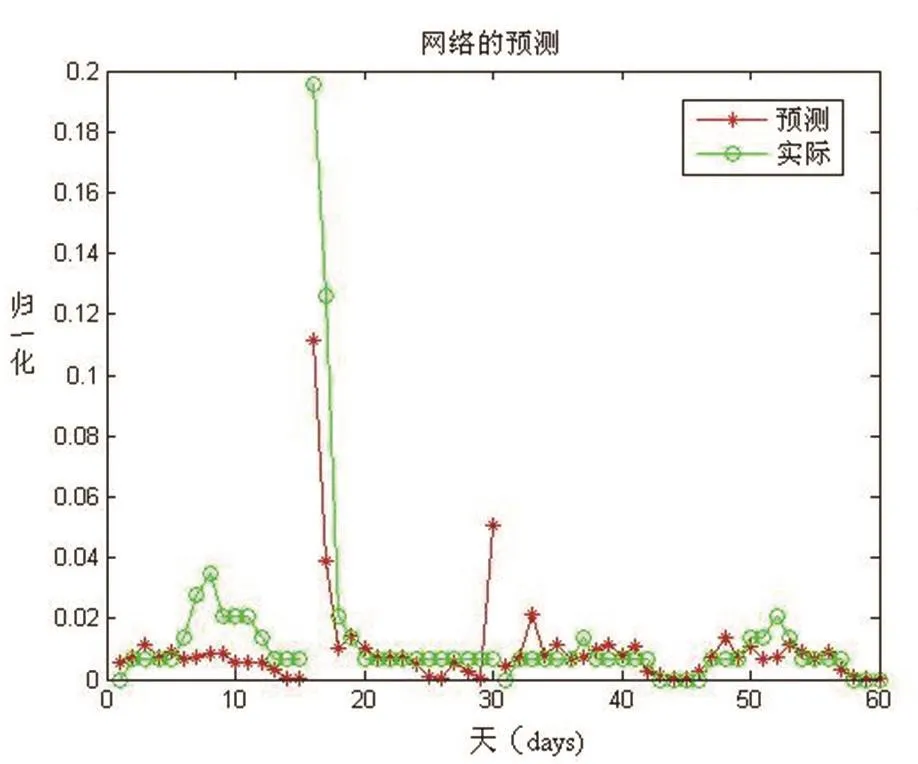
图3 模型预测值与实测值比较

经主成分分析后神经网络模型由原来780个输入变量降维为195个，仿真结果如图所示，网络的误差和泛化能力都得到了提高，对于咸潮的预测比较准确，可以作为工程应用方面的参考与指导。

4.3 神经网络模型

一般一个隐层的神经网络就可以任意逼近一个非线性函数，但是两个隐含层的神经网络其非线性的逼近能力更强，考虑到咸潮预报的非线性模型采用四层BP神经网，其中第一隐层节点数数经反复试验选择为69，Kudrycki的经验研究表明第一隐含层与第二隐含层节点数的最优比例应为3:1[5]，因此第二隐层节点数定为23，神经网络结构为105-69-23-15。传递函数采用正切函数，学习算法采用弹性BP方法。

仿真结果如图3所示，由仿真结果曲线可以看出，模型可以较好的反应盐度的变化情况，能够作为咸潮入侵预报做出指导。

表1 模型输入变量

5 结论

本文采用相关分析法和主成分分析法相结合的方法对输入的变量进行了选择，用神经网络进行了建模和预测。通过相关分析和主成分分析对输入的存在相关关系的多维变量进行了降维处理，提高了输入变量之间的相互独立性，由神经网络的仿真结果可以看出优化输入变量后的模型较好的预测了七堡未来15天咸潮的变化情况，为取水口的取水规划提供了有意义的参考。