一类非线性时滞细胞神经网络稳定性分析

李洁坤, 丁明智, 虞继敏

(1.柳州师范高等专科学校数学与计算机科学系 广西柳州545004; 2.广西师范学院数学与计算机科学系 广西南宁530023;3.重庆邮电大学数理学院 重庆400065)

一类非线性时滞细胞神经网络稳定性分析

李洁坤1, 丁明智2, 虞继敏3

(1.柳州师范高等专科学校数学与计算机科学系 广西柳州545004; 2.广西师范学院数学与计算机科学系 广西南宁530023;3.重庆邮电大学数理学院 重庆400065)

研究了一类常时滞细胞神经网络的全局渐近稳定性.通过构造适当的Lyapunov-Krasovskii泛函,利用线性矩阵不等式(LM I)得出了全局渐近稳定性判据.数值的例子验证了方法结果的有效性.

全局渐近稳定性;线性矩阵不等式;Lyapunov-Krasovskii泛函;时滞

0 引言

神经网络的全局渐近稳定、平衡点的存在性和唯一性、动力学特性受到许多专家学者的深切关注,并成功地应用到信息处理、图像处理、最优化问题、模式识别等问题中.同时神经网络中时滞现象又是客观存在的,有时是不可避免的,在研究的过程中常要考虑时滞的存在对整个网络稳定性的影响.时滞细胞神经网络稳定性分为两类:一类是时滞相关的[1-2];另一类是时滞无关[3]的.时滞无关的判据趋于保守,尤其是时滞较小时,而时滞相关通常具有较小的保守性.

文献[4]通过变换把神经网络系统变换成线性系统,然后构造Lyapunov函数得出全局渐近稳定的一个充分条件且该条件是时滞相关的.文献[5]引入自由权值矩阵得出两个全局渐近稳定性判据,一个与时滞相关,一个与时滞无关.文献[6]通过对Lyapunov范函导数上界进行估计,得出全局渐近稳定性的一个充分条件与时滞无关.本文通过构造具有增广形式的Lyapunov范函,利用牛顿-莱布尼兹公式,对系统方程引入自由权值矩阵,结合矩阵不等式技巧,得到了比文献[4-6]限制性更少、条件更为宽松常时滞神经网络的全局稳定性的充分判据.

1 神经网络模型

考虑如下的细胞神经网络模型

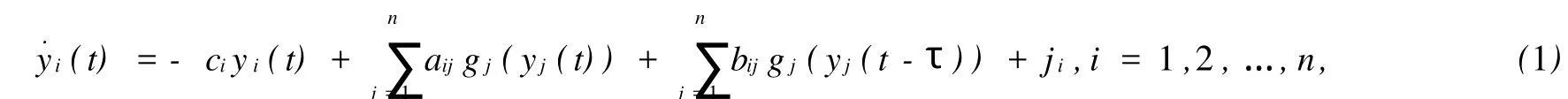
或者其等价形式

其中,y(t)=[y1(t),y2(t),…,yn(t)]T是状态向量,C是正定的对角矩阵,A=[aij]n×n,B=[bij]n×n分别表示状态反馈矩阵和时滞反馈矩阵,J=[j1,j2,…,jn]T是外部输入向量,τ>0为传输时滞,g(y(t))=[g1(y1(t)),g2(y2(t)),…,gn(yn(t))]T表示神经元的激活非线性向量函数.

(1)转化为模型

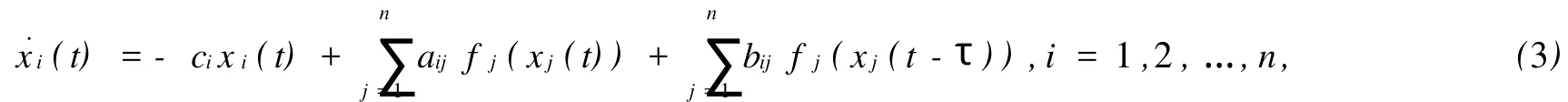
或等价的系统模型

其中,x(t)=[x1(t),x2(t),…,xn(t)]T是新的状态向量,f(x(t))=[f1(x1(t)),f2(x2(t)),…,fn(xn(t))]T是新的激活函数,并且有

系统(1)的平衡点y＊可以通过x(t)=y(t)-y＊平移到系统(3)的零点上.于是,系统(1)的平衡点y＊的全局渐近稳定性问题转化为系统(3)的关于零点的全局渐近稳定性问题.

2 主要结果

定理1在条件(5)成立的条件下,如果存在正定矩阵P,Q,Z,半正定对角矩阵Tj=diag(tj1,tj2,…,tjn)≥0, j=1,2,D=diag(d1,d2,…,dn)≥0,适维矩阵N=[NT1,NT2,NT3,NT4]T,使得矩阵不等式满足Θ<0,那么,系统(4)关于原点是全局渐近稳定的,且时滞相关的,

其中,

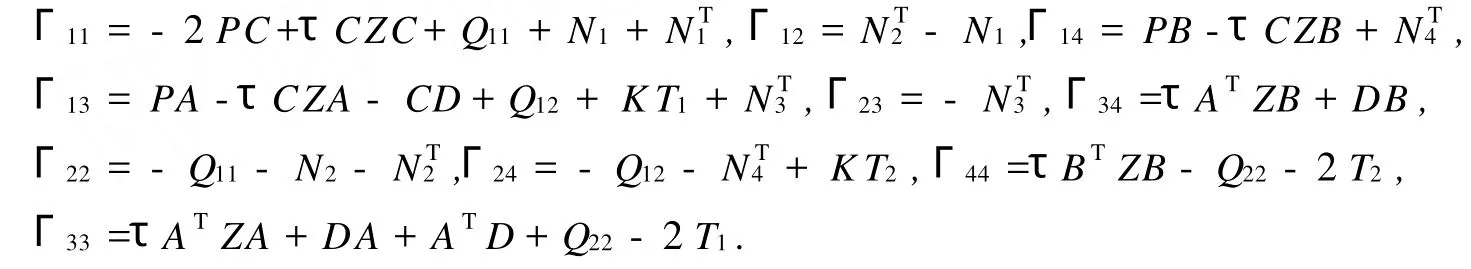
证明 构造Lyapunov-Krasovskii范函V=V1+V2+V3+V4,其中,

沿系统(4)的解轨线,计算Vi(i=1,2,3,4)关于时间的导数:

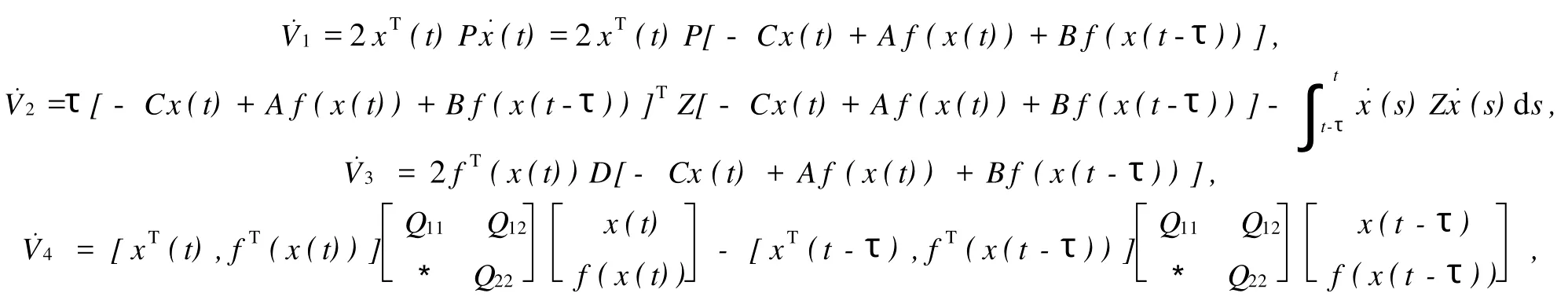
又由(5)有

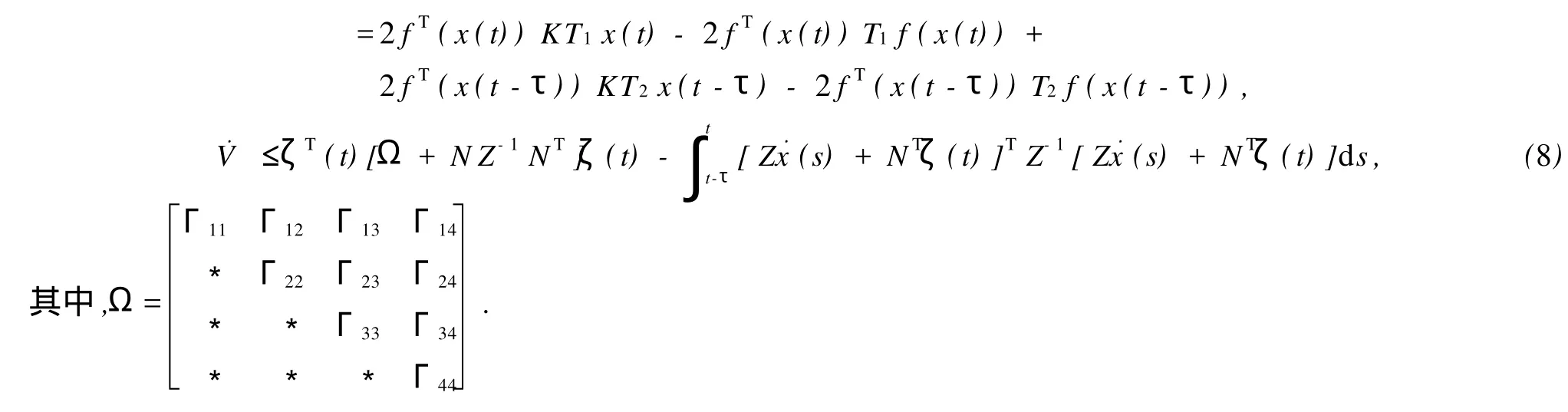
由式(6)和式(8)得˙V<ζT(t)(Ω+N Z-1NT)ζ(t)=ζT(t)Θζ(t)<0.从而,系统(4)关于原点是全局渐近稳定的,且时滞相关的.

为了说明得到的判据比以前结果的优越性,令Z=0,N=0得到系统(4)在原点时滞无关的全局稳定性判据.

推论1在条件(5)成立的条件下,如果存在正定矩阵P,Q,Tj=diag(tj1,tj2,…,tjn)≥0,使得矩阵不等式满足Θ<0,那么系统(4)关于原点是全局渐近稳定的.其中,

在推论1中,令Q11=0,Q12=0,T1=D,T2=0,得文献[6]的结论.

若令C=I,则(4)变为:

推论2如果存在正定矩阵P=[Pij]∈Rn×n,Q=[qij]∈Rn×n和半正定对角矩阵D=diag(d1,d2,…,dn)≥

如果保留˙x(t)项,利用系统(4)的方程引入自由权值矩阵,我们有定理2.

定理2在条件(5)成立的条件下,如果存在正定矩阵P,Q,Z,和半正定对角矩阵Tj=diag(tj1,tj2,…,tjn)≥0,j=1,2.适维矩阵N=[N1T,N2T,N3T,N4T,N5T]T和适维矩阵M=[M1T,M2T,M3T,M4T,M5T]T,使得矩阵不等式满足Θ<0,那么系统(4)关于原点是全局渐近稳定的,且时滞相关的.其中

证明 构造Lyapunov-Krasovskii范函如(7),类似定理1的证明(略).

在定理2中,我们令Z=0,N=0得到系统(4)在原点时滞无关的全局稳定性判据.

推论3在条件(5)成立的条件下,如果存在正定矩阵P,Q,半正定对角矩阵Tj=diag(tj1,tj2,…,tjn),j=1,

2,使得矩阵不等式满足Υ<0,那么系统(4)关于原点是全局渐近稳定的.其中,

在推论3中,如令M4=0,M5=0,T2=0,Q12=0,D=0,得类似文献[5]的结果.

推论4在条件(5)成立的条件下,如果存在正定矩阵P,Q,Tj=diag(tj1,tj2,…,tjn),j=1,使得矩阵不等式满足^Υ<0,那么系统(4)关于原点是全局渐近稳定的.其中,

3 举例及仿真

为了说明所得结果的有效性条件的宽松性,我们举例与先前文献的结果相比较.用matlab中DDE23程序求解时滞微分方程,用LM I工具箱求解定理中的线性矩阵不等式.

例1 考虑如下的时滞细胞神经网络系统,

应用推论1,通过matlab的LM I工具箱求得一个可行解:

图1 系统(10)时间状态响应曲线Fig.1 System(10)time response curve of the state

当初始值为(-1,1)、时滞为τ=127时系统(10)时间状态响应曲线如图1所示.因此,根据推论1～4知,该系统的平衡点是全局渐近稳定的,且与时滞无关的.而文献[4]的结果与时滞相关的,这就意味着我们的结果比文献[4]具有更少的保守性.

[1] Fridman E,Shaked U.An imp roved stabilization method fo r linear time-delay system s[J].IEEE Trans Automat,2002, 47:1931-1937.

[2] Fridman E,Shaked U.Delay-dependent stability and H control:constant and time-varying delays[J].Int J Control, 2003,76(1):48-60.

[3] Fridman E,Shaked U.Parameter dependent stability and stabilization of uncertain time-delay system s[J].IEEE Trans Automat,2003,48:861-866.

[4] 杨德刚.一种新的时滞细胞神经网络全局渐近稳定性准则[J].重庆师范大学学报:自然科学版,2007,24(3):46-50.

[5] Xu Junpin,Dao ying,Cao Yongyan.Delay-independent and delay-dependent stability of a novel delayed neural networks by Lyapunov functional based app roaches[C]//Proceedings of the 2006 American Control Conference.M inneapolis, 2006:3146-3151.

[6] Singh V.A generalized LM I-based app roach to the global asymp totic stability of delayed cellular neural networks[J]. IEEE Trans,2004,15:223-225.

Stability Analysis of Celluar Neural Networks with Delay

L IJie-kun1, D INGM ing-zhi2, YU Ji-min3
(1.Department of M athem atics and Com puter Science,L iuzhou Teachers College,L iuzhou 545004, China;2.Department of M athem atics and Com puter Science,Guangxi Teachers Education University, N anning 530023,China;3.College of M athem atics and Physics,Chongqing University of Posts and Elecomm unications,Chongqing 400065,China)

The global asymp totic stability of celluar neural networks w ith constant delay is studied.An app rop riate type of Lyapunov-Krasovskii functions and the linear matrix inequatity (LM I)app roach are p roposed to investigate the p roblem.An imp roved global asymp totic stability criterion is also derived.Numerical examp le demonstrates the effectiveness of the criterion.

global asymp totic stability;linear matrix inequatity;Lyapunov-Krasovskii functionals;delay

O 231.2

A

1671-6841(2010)03-0054-05

2010-01-18

重庆市自然科学基金资助项目,编号2009BB3280.

李洁坤(1967-),女,副教授,主要从事时滞系统控制研究,lzszljk@163.com.