切流式旋流器内两相流场的模拟

王振波,马 艺,金有海

(中国石油大学机电工程学院,山东东营 257061)

切流式旋流器内两相流场的模拟

王振波,马 艺,金有海

(中国石油大学机电工程学院,山东东营 257061)

将雷诺应力模型与欧拉分析方法相结合,对切流式单、双入口旋流器内的单相和两相流场进行模拟。模拟结果表明:与双入口旋流器比较,单入口旋流器内流场存在明显偏心现象,并且速度分布和湍流参数均存在偏差,流场很不稳定;对于油水两相流场,双入口旋流器的油相和水相体积分数径向变化梯度更大,油相更倾向于向轴心移动形成油核;双入口旋流器的工作性能优于单入口旋流器;试验结果验证了模拟结果的正确性。

水力旋流器;油水分离;数值方法;模拟;Fluent软件

水力旋流器的大多数应用场合中,流体流动呈高雷诺数下的湍流状态(水力旋流器的进口雷诺数高达 105～108)[1-2]。旋流器内湍流的存在不仅会引起分散相颗粒的湍流扩散,对分离性能产生不利影响,而且会造成旋流器内能量的损耗。近年来,利用数值模拟技术预测旋流器的流场和性能受到重视,但是数值模拟研究主要是针对旋流器内三维速度场,分析切向、轴向及径向速度,而对于反映旋流器内湍流流动的各项特征参数如湍动能和湍能耗散率等研究较少,另外旋流器内的油水分离过程也有待加强,从而更好地为结构优化提供理论依据。因此,笔者应用 Fluent软件,将湍流模型与多相流欧拉分析方法相结合,对切流式旋流器内油水分离过程进行三维模拟,分析旋流器内流场的分布规律和油水两相的分离特性,进行分离效率预测,并在此基础上进行入口结构优化。

1 湍流模型

湍流模型是油水分离 CFD数值模拟计算的核心[3]。对于水力旋流器来说,其内部流动规律复杂,呈现强湍流现象,而基于涡黏性假设的 k-ε模型及其修正模型都采用各向同性的湍动黏度来计算湍流应力,难于考虑旋转流动及流动方向表面曲率变化的影响,相应地,模拟结果有很大的局限性。雷诺应力模型RS M直接建立 Reynolds应力微分方程,并通过对方程中各项进行模化封闭,直接求解出流场中各项流动参数的分布情况,更适合于复杂强旋流场的计算。因此本文中采用RS M模型作为基本的湍流模型对旋流器进行数值模拟。相对应的方程有[4]:

式中,DL,ij为分子黏性扩散项;pij为剪应力产生项; Fij为系统旋转产生项;DT,ij为湍流扩散项;φij为压力应变项;εij为黏性耗散项。

补充 k和ε方程如下:

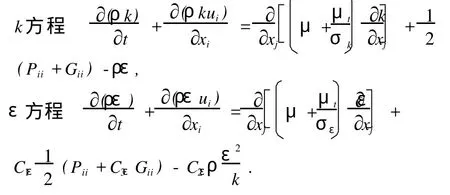
这样就构成了三维湍流流动问题的基本控制方程组。

考虑到目前用于研究多相流的方法有欧拉 -拉格朗日方法和欧拉 -欧拉方法[5],对于第二相比较多的情况,可把第二相当成连续相,一般采用欧拉 -欧拉方法,可用的多相流模型有VOF模型、混合模型和欧拉模型。根据 FLUENT用户指南,认为采用混合模型(M IXTURE)模拟比较合适。具体控制方程及处理方法可参见文献[6]。

2 计算模型及相关设置

2.1 几何模型、网格划分

图 1 切流式单入口旋流器的结构示意图Fig.1 Schematic diagram of structures of single-inlet tangential hydrocyclone

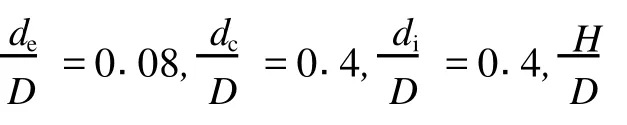
2.2 相关设置

材料设置:混合物采用油水混合液,主相为水,次相为油。水的物性参数直接取 Fluent数据库中的值,ρw=998.2 kg·m-3,μw=0.001003 Pa·s,油的物性参数根据实验参数取得:ρo=850 kg·m-3,μo=0.050 Pa·s。相间的拖拽力为 Schiller-Naumann模型,滑移速度为Manninen-at-al模型,质量传输函数为 constant。

边界条件:入口边界采用速度入口,入口流量为3 m3·h-1;出口边界按照湍流流动充分发展处理;壁面边界采用无滑移边界条件。同时设定油相体积比为10%。

数值解法:采用有限体积法控制方程的离散,选取QU ICK的差分格式,对流动时均控制方程组的数值求解采用 SI MPLEC算法,压力差补格式为 PRESTO!格式。

计算策略:先计算单相流体的流动情况,首先利用 RS M模型进行定常情况下的计算,之后改为非定常至计算稳定,然后在此基础上再运用M IXTURE模型加入第二相进行油水两相流场的计算。

3 模拟结果分析

3.1 入口部分流体流动

旋流器的入口结构对后续流场的分布有直接影响,所以有必要对旋流器的入口部分的流场变化进行分析。图 2为切流式单入口旋流器的入口截面矢量及入口流线图 (图 2(a)中心空白位置为溢流管外壁)。由图 2(a)可以看到,流体沿切向进入分离空间,在圆柱腔内产生高速旋转流场,以便在超重力场下进行两相分离。同时可以看出,旋流器入口侧 (X轴下方)的速度矢量分布密度要明显大于另一侧,即入口截面部分的流场已表现出了不均匀性,总体的旋转是偏向入口一侧的,流体流动的旋转中心无法与腔体的物理中心相重合。这一点可以通过入口部分的流线(图 2(b))进一步证明,显然也不可避免地会作用于旋流器内主要分离空间的流场。

图 2 切流式单入口旋流器入口截面矢量图及入口部分流线图Fig.2 Section vectors and stream line of inlet section in single tangential hydrocyclone

3.2 入口部分结构优化

图 3 切流式双入口结构示意图Fig.3 Schematic di agram of structure of double tangenti al inlets

流场的不对称性显然是由旋流器的单入口结构导致的,还有进一步优化的空间。贺杰等[7]曾经针对液 -液水力旋流器对单入口和双入口两种情况下旋流器的分离性能进行对比实验,发现双入口的分离性能要大大优于单入口的。因而在此基础上提出了切流式双入口进料的概念,其基本入口形式如图3所示,其他结构不变。显然两入口在空间上呈对称分布,从结构上避免了偏心现象的发生。进一步通过模拟主要分离空间的流场分布规律来比较单入口与双入口旋流器内的流动稳定性与分离效果。

3.3 主要分离空间的流场

以旋流器入口顶部截面为基准 (z=0),选取锥段中部截面 z=-350 mm作为研究截面。

图 4为两种旋流器切向速度、轴向速度、湍动能和湍能耗散率的分布。由图 4可以看到,两种旋流器的切向速度分布规律基本相同,呈现出明显的组合涡形式,基本趋势为从边缘向中心不断增大,在达到最大值(r=10 mm附近)后又迅速降低,并以此最大值为界分为准自由涡区和强制涡区,但是相对来说,显然双入口结构的切向速度最大值 (10.1 m/s)要大于单入口结构的切向速度最大值 (8.95 m/s),相应地产生的离心力更大,流体的分离效果也更优。同时单入口结构的切向速度呈现出了明显的非轴对称性,切向速度的最小值处于 r=1.29 mm处,与旋流器的中心轴线有较大偏离。

两种旋流器的轴向速度分布规律也基本相同,呈近壁下行流和近轴上行流分布,在轴心处达到最大值,在边壁附近存在最小值,并在约二分之一半径处存在零点。单入口与双入口两种结构旋流器的轴向速度在数值上相差不大,其中双入口结构的轴向速度最大值和最小值的平均值分别为 1.86 m/s和-1.72 m/s,单入口结构则为 2 m/s和 -1.83 m/s。然而,相比双入口结构旋流器对称性良好的轴向速度分布,单入口旋流器的轴向速度在轴心两侧的最小值相差较大,左侧 r=-14 mm处为 -2.44 m/s,右侧 r=-13.9 mm处为 -1.22 m/s,表现出了明显的速度分布不均现象。

两种旋流器的湍动能分布均是在边壁附近最大,之后随着半径的减小而迅速减小。以双入口旋流器为例,湍动能在 r=16 mm处达到最大值 1.38 m2/s2,之后在轴心附近 r=1.35 mm处已减为 0.45 m2/s2,这是因为湍动能主要来源于时均流,通过雷诺切应力做功给湍流提供能量,也说明湍流在水力旋流器的边壁附近区域从时均流中提取的能量较多。通过湍动能表达式 k=1.5(¯uI)2可以进一步看出湍动能 k与时均流速 ¯u和湍流强度 I的平方成正比。这也是双入口旋流器的湍动能总体上要大于单入口旋流器的原因。

湍能耗散率的分布规律与湍动能分布规律类似,即湍动能较大的地方湍能耗散率也较大,反之亦然。显然,湍动能和湍能耗散率的较大值一般出现在流态变化复杂,涡旋活动剧烈的强湍流区,具体表现为在旋流管器壁附近。这表明,旋流管内湍流能量的产生和耗散与流体状态的变化程度密切相关。对于两种旋流器来说,双入口旋流器的湍能耗散率 也更大。

图 4 旋流器内 z=-350 mm处的流动参数分布Fig.4 Flow parameters distribution on section-350 mm of hydrocyclone

通过对两种旋流器主要分离空间的主要流动参数分布进行比较分析,可以发现单入口旋流器内流场存在明显的偏心现象,并且速度分布与湍流参数均与双入口旋流器存在偏差,以至于一方面流体流动不稳定,整个旋流器工作状况变差,内旋流的流体也不能很好地从溢流口流出,并且容易产生涡流与返混,另一方面流体所受离心力偏小,分离情况也会随之减弱。所以,从旋流器内流场来看,双入口旋流器的工作性能要优于单入口旋流器。

3.4 主要分离空间的两相浓度分布

为了进一步了解旋流器的分离性能,更真实地分析油水两相的分离情况,在单相流场基础上加入油相进行两相流动的模拟研究。其中入口油相体积分数为 10%,仍然选取 z=-350 mm截面为研究截面。两种旋流器在此截面上的油相与水相浓度分布如图5所示。

图 5 旋流器内 z=-350 mm处的两相体积分数分布Fig.5 Two-phase volume fraction distribution on section-350 mm in hydrocyclone

因为进入旋流器的油水混合液受到离心力作用,油相向中心聚集,而水相则向边壁移动,所以由图 5可以看出,两种旋流器的两相分布规律是相似的,均是随着半径的减小,油相体积分数呈现增加趋势,而水相体积分数则逐渐减小。但是,相对来说,在轴心附近双入口旋流器的油相体积分数要大于单入口旋流器的,而在边壁附近则相反,这就意味着双入口的油相体积分数径向变化梯度更大,油相更倾向于向轴心移动,形成油核,分离效果更好。对于水相体积分数来说,则相反。这一结果验证了单相流场的比较结果。

3.5 分离性能对比

分离效率是衡量分离性能的重要指标。在得到旋流器内流场、各相体积分数分布后,便可估算出旋流器的分离性能。水力旋流器的分离效率定义为

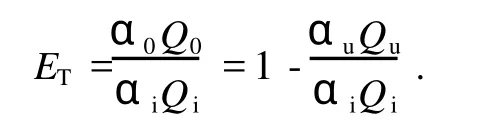
式中,下标 i,o,u分别代表来流入口处及顶部出口、底部出口处的参数;α为油相体积率;Q为流量。

为了验证结果的正确性和更深一步了解分离性能,这里对两种旋流器分别进行性能试验,其试验流程如图6所示。

因为流量和溢流率是影响分离效率的重要参数,所以在此分别考虑溢流率为 10%时流量对分离效率的影响和流量为 3 m3/h时溢流率的影响。两种旋流器的试验值与模拟值的对比如图 7所示。

图 6 旋流器性能试验流程图Fig.6 Experi ment flow diagram of separation performance of hydrocyclone

图 7 旋流器的分离效率曲线Fig.7 Separation efficiency curves of hydrocyclone

从图 7中可以看出,数值模拟结果与试验研究结果比较接近,基本分布规律一致:①随着流量增大,切向速度和离心加速度都增大,分离效率也逐渐增加,但在流量大于 3 m3/h时,试验值开始呈现下降趋势,这是由分散相液滴受到的剪切应力过大而发生破碎,不利于分离而导致的,而模拟值则仍在增大,这是因为在模拟过程中,很难完全考虑液滴的聚结破碎等因素,这也导致了模拟值整体上要略大于试验值;②随着溢流率增加,分离效率也在增加,但是可以看到与入口流量相类似,溢流率也存在一个合理工作区,当溢流率大于 15%时,虽然能耗有所减小,但是分离效率也开始下降,所以一般工业应用的溢流率值比较小。

从图 7可以看到,双入口旋流器的分离效率均大于单入口旋流器的,这充分说明了双入口旋流器的分离性能优于单入口旋流器的,所以在空间满足要求的条件下,在工业上采用双入口旋流器进行油水分离为更好的选择。

4 结束语

切流式单入口旋流器流动不均匀,流场很不稳定,提出双入口旋流器以进行入口数目优化。对于单相流场来说,单入口旋流器的主要分离空间内流场存在明显偏心现象,并且速度分布和湍流参数均存在偏差,而双入口旋流器流场则呈现很好的轴对称分布。对于两相流场来说,双入口旋流器的油相和水相体积分数径向变化梯度更大,油相更倾向于向轴心移动,相应地分离效率也更大,双入口旋流器的工作性能优于单入口旋流器的。

[1] 金有海,马艳杰,许伟伟,等.排气芯管结构对导叶式旋风管内流场影响的数值模拟[J].中国石油大学学报:自然科学版,2009,33(6):87-90.

J I N You-hai,MA Yan-jie,XU Wei-wei,et al.Numerical simulation of effects of vortex finder on gas phase flow in cyclonewith guide finder[J].Journalof ChinaUniversity of Petroleum(Edition of Natural Science),2009,33 (6):87-90.

[2] NOWAKOWSKIA F,DYAKOWSKI T.Investigation of swirling flow structure in hydrocyclones[J]. Trans IchemE,81(A):862-873.

[3] 牛贵锋,艾志久,刘春全,等.油水旋流分离器流动机理和分离性能研究 [J].石油矿场机械,2007,36 (9):13-17.

N I U Gui-feng,A I Zhi-jiu,L I U Chun-quan,et al.Study on flow mechanis m and separation performance of oil-water separation hydrocyclone[J].Oil Field Equipment, 2007,36(9):13-17.

[4] 王福军.计算流体动力学分析[M].北京:清华大学出版社,2004.

[5] 王瑞金,张凯,王刚.Fluent技术基础与应用实例[M].北京:清华大学出版社,2007.

[6] SLACKM,COKLJATD,VASQUEZ SA.Reynolds——stressmodel for Eulerian multiphase:Proc 4th Int Symp on Turbulence Heat and Mass Tralqsfer[C].Begell House Inc,2003:1047-1054.

[7] 贺杰,蒋明虎,宋华.新型油水分离装置——水力旋流器试验[J].石油机械,1993,21(12):26-29.

HE Jie,J I ANGMing-hu,SONG Hua.Experiments of a new type of oil-water separation device—hydrocyclone [J].China Petroleum Machinery,1993,21(12):26-29.

(编辑 沈玉英)

Si mulation of two-phase flow field in tangential hydrocyclone

WANG Zhen-bo,MA Yi,J IN You-hai
(College of Electrom echanical Engineering in China University of Petroleum,Dongying257061,China)

RS M and Eulermethod were combined to study the single-phase and two-phase flow field in tangential hydrocyclones.The results show that compared with double-inlet hydrocyclone,single-inlet hydrocyclone had eccentricity in the flow field,and there were differences in velocities and turbulent parameters,and the flow field was unstable.For the oil-water flow,the radial gradients of volume fractions of oil and water in double-inlet hydrocyclone were larger.The oilwasmore inclined to move to the axis and formed oil-core.Thework performance of double-inlet hydrocyclonewas better than thatof single-inlet hydrocyclone,and the correctness of the simulation was verified.

hydrocyclone;oil-water separation;numericalmethods;simulation;Fluent software

TQ 051.8

A

10.3969/j.issn.1673-5005.2010.04.027

1673-5005(2010)04-0136-05

2009-12-03

国家“863”高技术研究发展计划项目(2007AA09Z318)

王振波(1971-),男(汉族),山东寿光人,副教授,博士,主要从事石油化工过程装备、多相流分离技术的教学、科研及设计工作。