考虑后期变形影响的高面板堆石坝工作性态

王永明,董育烦,朱 晟

(1.河海大学水利水电学院,江苏南京 210098;2.中国水电顾问集团华东勘测设计研究院,浙江杭州 310014)

考虑后期变形影响的高面板堆石坝工作性态

王永明1,董育烦2,朱 晟1

(1.河海大学水利水电学院,江苏南京 210098;2.中国水电顾问集团华东勘测设计研究院,浙江杭州 310014)

由于面板堆石坝工作条件复杂,受到尾水位升降等干湿循环的影响会产生湿化变形;又由于堆石料处在高坝高应力状态下,会导致由颗粒破碎引起随时间变化的流变变形。认为高坝有限元计算必须考虑这两者引起的后期变形的影响。对某超高混凝土面板堆石坝进行了考虑后期变形与不考后期变形的对比计算,结果表明后期变形较大程度上改变了大坝的变形和应力,对面板变形和应力影响甚大。

面板堆石坝;湿化;流变;后期变形

近年来,随着超重型振动辗压设备和混凝土面板滑模浇筑技术的研制成功,堆石体因变形过大而导致的面板开裂问题得到改善。高面板堆石坝具有明显的经济性、安全性,因而成为坝工界的首选坝型,发展迅猛,已建成天生桥一级、Campos-Novos、洪家渡、水布垭等一大批200m级的高坝。对面板堆石坝的数值模拟已由原来的二维线弹性模型进入到三维弹塑性模型分析,对有限元的运用已进入日臻精细的程度,但仍存在不少问题。已建成坝的资料表明,数值计算与原型监测资料相去甚远,这主要有2个方面的原因:①现阶段有限元计算所采用的本构模型参数仍然基于室内三轴试验,而室内三轴试验试样是原型级配料的缩尺,级配的变化导致参数具有不可预测的影响,缩尺效应尚未完全解决。②后期变形的影响,后期变形主要包括堆石的湿化和流变变形。由于堆石料在填筑过程中受到降雨的淋滤,水库在建成以后的初次蓄水、地下水位的上升、库水位的反复升降、面板止水的失效等原因都会使坝料颗粒浸水发生软化,棱角破碎,产生相互滑移,从而导致体积缩小。已有资料表明,堆石具有明显的流变特性,在高应力状态下堆石体内部颗粒破碎导致颗粒旋转、滚动和滑移,使得内部应力重新分配和颗粒位置的重新界定,这将引起一个与时间相关的附加变形,一般在大坝竣工蓄水数年后变形才能稳定,这就是堆石料的流变特性,而且流变变形占到总变形量的1/4。因此,为了更合理地预测高面板堆石坝的工作性态,为设计和安全校核服务,必须计入后期变形的影响,本文主要讨论后期变形的影响。

1 湿化变形试验方法

浸水变形试验可分为单线法和双线法2种。最早提出双线法的是Nobari等[1-2],所谓双线法是指分别进行干态和湿态下的试验,得到相应的应力应变关系,然后用相同应力状态下湿态与干态变形的差值作为该应力状态下发生浸水湿化时的湿化变形量。图1为双线法示意图,图中 Δεwij为湿化变形量。国内最早开展单线法试验研究的是沈珠江院士,他建立了相应的浸水湿化模型[3]。所谓单线法是指在干态下沿某一加载路径达到某一应力状态,然后在保持应力状态不变的条件下进行浸水湿化饱和,此过程中发生的变形即为该应力状态下的湿化变形量。图2为单线法示意图。

图1 双线法示意图

图2 单线法示意图

用初应变法进行有限元计算。将湿化单元在某一应力状态下所能产生的湿化变形当作该单元所具备的初应变势,然后将该初应变转化为该单元节点的等效节点力,求解所得的单元应变即为满足单元之间协调率的真实应变。

由于双线法改变了水与荷载对土体的作用顺序,这样的应力状态与实际不符;单线法符合浸水变形的实际过程,但1个试样只能得到1种应力状态下的湿化变形,要得到不同应力状态下的湿化变形,必须做多次试验,且考虑到试验结果的离散性等因素,试验工作量很大。笔者选用单线法进行试验研究。

2 流变模型

筑坝堆石料具有明显的流变特性,对大坝进行设计、分析时必须计入流变效应的影响,沈珠江等[4]对西北口面板堆石坝垫层料进行了长达数月的流变试验,开启了堆石流变试验与流变模型研究的先河,而后其建立的三参数指数模型[5]被广泛应用于土石坝的分析计算,被证明具有较好的适应性和参数稳定性。

选用该三参数指数模型,采用滞后变形理论并考虑堆石料的蠕变特性,用初应变法计算土体的黏滞荷载,用指数型曲线表示堆石料的流变特征:

相应的应变速率为

式中:ε为时间为t时所产生的流变量;εf为t→∞时的最终流变量,与应力状态有关;c为t=0时单位时间流变量占εf的比值;﹒ε为流变速率。

对堆石材料而言,其最终体积流变和最终剪切流变与应力状态之间有不同的关系。根据试验研究结果,最终体积流变与最终剪切流变的计算公式如下:

式中:εvf为最终体积流变;σ3为围压 ;εsf为最终剪切流变;Pa为单位大气压,Pa=105Pa;Sl为应力水平;b和d为参数,b相当于σ3=Pa时的最终体积流变量,d相当于Sl=0.5时的最终剪切流变量。

计算时,将体积流变、剪切流变按Prandtle-Reuss流动法则转换成六分量应变张量。

3 工程实例

某混凝土面板堆石坝坝顶高程为409.00m,坝顶轴线长660 m,最大坝高为 233 m,坝顶宽度为12m,防浪墙顶高程为410.20m,墙高为5.4m。大坝上游坡度为1∶1.4,下游平均坡度为 1∶1.4。现已蓄水至380.00m。为模拟大坝分期填筑与蓄水过程,大坝共分40级加载,有限元模型共剖分为9694个单元和12462个节点,大坝有限元网格见图3。

3.1 瞬时变形计算模型及参数

采用土石坝计算中运用最为广泛的邓肯E-B非线性弹性模型[6],认为应力应变关系符合广义胡克定律,采用切线弹性模量和切线体积模量进行增量法计算,切线弹性模量和体积模量分别为

式中:Et为切线弹性模量;φ为非线性强度,φ由φ0,Δφ确定;Bt为体积模量;C,K,n,Rf,Kb,m为E-B模型参数。各计算参数来源于该坝前期可行性研究阶段的三轴试验和现场大型承压试验[7],如表1所示(C取零)。

表1 各坝体分区的E-B模型参数

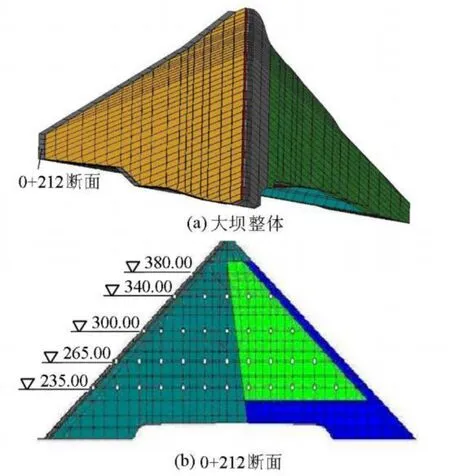
图3 大坝有限元网格(单位:m)

3.2 湿化计算参数

单线法符合浸水变形的实际过程,但1个试样只能得到1种应力状态下的湿化变形,要得到不同应力状态下的湿化变形,必须做多次试验。试验结果具有一定的离散性,但整体规律明显,见图4～5。由图4～5可知,湿化剪切应变与应力水平呈现较好的双曲线关系,而湿化体积应变与试验平均正应力亦呈现较好的双曲线关系。

图4 湿化剪切应变与应力水平的关系曲线

计算采用以下双曲线函数:

图5 湿化体积应变与平均正应力的关系曲线

3.3 流变参数的确定

由于室内堆石流变试验研究必须进行缩尺,包括试样的缩尺和时间的缩尺,但由于缩尺后堆石料的流变机理与原型的流变机理有差异,导致室内流变试验的变形时间较短,易于稳定,而且室内试验也难以合理模拟现场堆石的加载路径,因此室内流变试验成果仅能用作最终流变量的参考,而不能直接用于有限元计算。根据大坝原型的变形观测资料进行反演分析是研究流变的较好方法[5]。

表2给出了4个已建工程反馈所得的流变参数,其堆石岩性各不相同,具有一定的代表性[5]。考虑到该混凝土面板堆石坝的堆石料主要为灰岩,其岩性类似于鲁布革心墙堆石坝,暂时选用与鲁布革心墙堆石坝材料一致的流变参数。由于目前对堆石流变的研究尚不精确,故未对各分区的堆石料流变参数进行区分。

表2 已建工程反馈所得流变参数

3.4 计算结果分析

实际运行中若面板发生裂缝,需计算坝体内部浸润线,将浸润线以下的单元设置为湿化状态。现假定面板防渗功能完好,认为下游尾水位以下的单元均处于湿化状态。该坝从2003年1月开始填筑,至2007年 8月蓄水,工期历时近 5 a,蓄水至380.00m高程2a后在不考虑后期变形与考虑后期变形2种情况下对堆石体变形、应力,面板变形、应力以及面板缝的变形进行较为详细的对比分析。

3.4.1 堆石体的变形、应力

不考虑后期变形:蓄水至380.00m高程后,堆石体向上游的最大位移为7.9cm,位于0+212断面上游主堆石区高程230.00m附近位置,向下游的最大位移为47.4cm,位于下游次堆石区高程318.00m附近位置;最大竖向位移为180.4cm,发生在0+212断面318.00m高程附近的次堆石区域,占坝高的0.77%。坝体应力从坝顶向坝基呈现逐渐增大的趋势,蓄水后大、小主应力等值线在上游堆石区都出现上抬现象,极值所处的位置向上游主堆石区靠近。0+212断面堆石体第一主应力最大值为3.51MPa,第三主应力最大值为1.26MPa。

考虑后期变形:堆石的流变使坝体变形的分布规律改变不大,但数值明显增大。堆石体向上游的最大位移为13.4 cm,向下游的最大位移增至70.2cm;最大竖向位移为266.6cm,发生在325.00m高程附近的次堆石区域,占坝高的1.14%。应力的分布规律与不考虑后期变形时的相似,第一主应力最大值为3.36MPa,第三主应力最大值为1.06MPa。

由此可见,考虑后期变形后,水平变形和竖直变形均有较大幅度的增大,但分布规律相似,极值出现位置基本相同,只是竖向位移略微靠近坝体上部,这主要是由于流变变形具有滞后效应。是否考虑后期变形主应力亦差别不大,考虑后期变形后坝体应力略有松弛,且分布更为均匀。

3.4.2 面板的变形、应力

不考虑后期变形:水库蓄水后,面板变形的分布规律较好,面板挠度基本指向坝内,面板中下部约1/3～1/2坝高部位数值较大,最大值为42.4 cm,出现在河床剖面的265.00m高程附近。在水压力作用下,面板绝大部分区域表现为受压状态。其中顺坡向压应力最大值为5.8MPa,出现在0+212～0+228号断面面板中部的280.00m高程附近;坝轴向压应力最大值为4.0MPa,位于河床坝段的0+212断面275.00m高程附近。仅在面板的端部以及两岸存在局部拉应力区,顺坡向拉应力最大值为2.5MPa,位于河床坝段面板的底部,坝轴向拉应力出现在两岸,最大值为2.0MPa。

考虑后期变形:面板挠度分布规律基本不变,最大值增大为64.6 cm。面板应力的分布规律变化不大,但数值有较大的改变,其中顺坡向压应力最大值增大为11.9MPa,坝轴向压应力最大值为8.3MPa。两岸的坝轴向拉应力最大值增至4.3MPa。

由此可见,考虑后期变形后,面板挠度和应力值增加明显,说明在水荷载作用方向坝体产生较为明显的后期变形,导致面板跟随坝体移动,面板应力急剧增加,且面板和垫层出现脱空现象,罗马尼亚的LESU坝[8]就是因为面板与坝体后期变形不协调导致面板被卡在岩基上而被压碎,设计中应注意。

3.4.3 面板接缝的变形

不考虑后期变形:蓄水后,面板竖缝的变形有所增大。垂直缝长方向的沉降较小,最大不超过0.9cm,位于右岸剖面面板的底部;沿缝长方向的错动位移最大值为2.5cm,发生在右岸剖面面板下部;河床部位的竖缝全部呈压紧状态,两岸的面板缝为张拉状态,张开位移最大值为1.7cm,处于岸坡地形变化较大的位置;压缩位移最大值为1.8cm,发生在河谷中央剖面的250.00～260.00m高程部位。周边缝基本处于拉伸状态,最大张拉量为0.9cm,发生在河床0+212断面。

考虑后期变形:垂直缝长方向的沉降较小,最大值为1.1 cm;沿缝长方向的错动位移最大值为3.2cm,发生在右岸面板下部;河床部位的竖缝全部呈压紧状态,两岸的面板缝为张拉状态,张开位移最大值为2.7cm,处于岸坡地形变化较大的位置;压缩位移最大值为3.0cm,发生在河谷中央剖面。周边缝基本处于拉伸状态,最大张拉量为1.9cm,发生在河床0+212断面。

由此可见,考虑后期变形后,面板缝的变形更为剧烈,张性缝和压性缝最大变形均增加较大,其中面板竖缝的张开值和压缩值分别达到2.7 cm和3.0cm,周边缝拉开1.9cm,设计时应保证缝间的止水材料具有足够的安全余度,特别是压性缝必须填充合适的柔性材料以消散后期变形压应力产生的能量,以避免面板压碎性结构裂缝的产生。

4 结 论

a.由于高面板堆石坝运行条件复杂,受水位升降等干湿循环因素影响,计算中必须计入堆石料湿化变形的影响。

b.高面板堆石坝的施工历时数年,室内试验和已有监测资料表明,高面板堆石料具有明显的流变特性,因此计算中必须计入流变变形的影响。

c.对某超高混凝土面板堆石坝进行了是否考虑湿化和流变等后期变形影响的对比计算,计算结果表明,后期变形对坝体变形、应力分布规律略有改变,但变形、应力值增加明显,考虑后期变形后,面板应力增加剧烈,坝体运行状态趋于危险。

d.后期变形使得面板缝变形极值增加,设计时应对止水材料保留充分的安全余度。

[1]NOBARI E S, DUNCAN J M.Movements in dams due to reseervior filling [C]//ASCE Specialty Conference on Performance of Earth and Earth Supported Structures.Pbrdue :Purdue University , 1973:32-54 .

[2]NOBARI E S , DUNCAN J M .Static analysis of embankment dams:a finite element perspective [J].Dam Engineering ,1973, 1(21):79-99.

[3]左元明, 沈珠江.坝料土的浸水变形特性研究[R].南京:南京水利科学研究院土工研究所, 1989.

[4]沈珠江, 左元明.堆石体流变试验研究[R].南京:南京水利科学研究院土工研究所, 1983.

[5]沈珠江, 赵魁芝.堆石坝流变变形反馈分析[J].水利学报, 1998 , 6(6):1-6 .

[6]DUNCAN J M, CHANG C Y.Nonlinear analysis of stress and strain in soils[J].J of the Soil Mech and Found , 1970 , 96 (5):1629-1653.

[7]朱晟, 梁现培, 冯树荣.基于现场大型承载试验的筑坝原级配堆石料力学参数反演研究[J].岩土工程学报,2009 , 31(7):1138-1143.

[8]傅志安, 凤家骥.混凝土面板堆石坝[M].武汉:华中理工大学出版社, 1993.

Working behaviors of high concrete face rockfill dams considering late deformation

WANG Yong-ming1,DONG Yu-fan2,ZHU Shen1(1.College of Water Conservancy and Hydropower Engineering,Hohai University,Nanjing210098,China;2.East China Investigation&Design Institute of HydroChina Corporation,Hangzhou310014,China)

The concrete face rockfill dams have complex working conditions and will result in wetting deformation owing to the influencesof drying and wetting cycles such as variation of tailwater levels.Owing to the rockfill materials under high stress conditions,the time-dependent rheological deformation of high concrete face rockfill dams will be induced by the particle breakage.It was regarded that the late deformation induced by the above two factors should be considered for the calculation of high dams by use of finite element methods.A comparative calculation was performed for a high concrete face rockfill dam with and without consideration of late deformation.The results show that the late deformation greatly changes the stress and deformation of the dam and has significant influences on the deformation and stress of the concrete faces.

concrete face rockfill dam;wetting;rheological deformation;late deformation

TV641.4

A

1006-7647(2010)03-0024-04

10.3880/j.issn.1006-7647.2010.03.007

王永明(1983—),男,湖南益阳人,博士研究生,从事土石坝等水工建筑物研究。E-mail:wym247@163.com

2009-06-09 编辑:骆超)