低渗透介质中3种井的非线性渗流流量

邓英尔,刘慈群,张 伟

(1.成都理工大学地质灾害防治与地质环境保护国家重点实验室,四川成都 610059;2.中国科学院渗流流体力学研究所,河北廊坊 065000)

低渗透介质中3种井的非线性渗流流量

邓英尔1,刘慈群2,张 伟1

(1.成都理工大学地质灾害防治与地质环境保护国家重点实验室,四川成都 610059;2.中国科学院渗流流体力学研究所,河北廊坊 065000)

给出考虑起始水力梯度的低渗透介质中分别存在垂直井、垂直裂缝井及分支水平井时的非线性渗流量公式,讨论了非线性渗流参数(起始水力梯度)、供给边界、垂直裂缝井的裂缝半长、分支水平井井筒数等因素对流量的影响。结果表明:在其他条件相同时,非线性渗流使得垂直井、垂直裂缝井及分支水平井流量降低;供给边界距离越大,垂直井、垂直裂缝井及分支水平井流量越小;垂直裂缝井的裂缝越长,流量越大;井筒数越多,分支水平井流量越大。

非线性渗流;垂直井;垂直裂缝井;分支水平井;低渗透介质;起始水力梯度

在建筑工程中,常用明沟排水法、深井法等方法降低地下水位。文献[1]介绍了通过水平井降低地下水位的原理与施工技术。水平井是一种很有前景的新技术[1-3],在薄的或低渗透介质中开采(或疏干)地下水等地下流体时比垂直井有较大的优势[2-3],故受到水文地质、环境工程及石油工程等领域研究者的高度重视[3-5]。对于地下水水平井井流的计算可追溯到Hantush等[6]对辐射井流的研究(可视为1组水平井),他们用等强度线汇刻画水平井管。此后,研究者广泛采用线汇描述水平井管的作用[4-13]。水力压裂是改善地层渗透性、提高流量的有效手段之一,该技术在工程中得到了广泛应用[2]。

自从1856年达西渗流定律建立以来,该定律被广泛运用于地下水、石油、天然气等开发领域[13-16]。渗流理论已成为人类开发地下水等诸多地下流体资源的重要理论基础,在保护环境、防治地面沉降、兴建水利水电工程等领域成为必不可少的理论。然而,有许多情形涉及非线性渗流,例如低渗透介质渗流问题[13-18]。笔者研究低渗透介质中垂直井、垂直裂缝井及分支水平井的非线性渗流问题,给出考虑起始水力梯度的垂直井、垂直裂缝井及分支水平井非线性定常渗流流量公式,分别计算低渗透介质中这3种井的非线性渗流流量,讨论非线性渗流参数(起始水力梯度)、供给边界、垂直裂缝井的裂缝半长、分支水平井井筒数等对流量的影响,为低渗透介质中分别存在垂直井、垂直裂缝井及分支水平井时的非线性渗流量计算提供依据。

1 低渗透介质非线性渗流定律

低渗透介质渗流时,可近似按照具有起始水力梯度的非线性渗流定律进行描述,即

式中:v为渗流速度,m/s;u为压力,Pa;ρ为密度,kg/m3;Ji为起始水力梯度;K为渗透系数,m/s。

2 低渗透介质中3种井的非线性渗流流量公式

2.1 垂直井

当垂直井工作时,在地层中产生平面径向渗流。根据低渗透介质非线性渗流方程,可得低渗透介质中垂直井的径向非线性渗流流量:

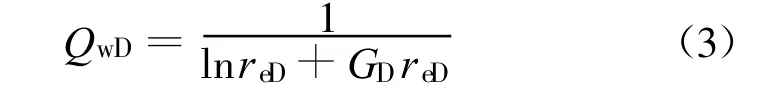
其中各无量纲量的定义为

式中:Q0为初始状态的流量;M为含流体低渗透介质厚度,m;r为径向半径,m;下标w为井壁、D表示无量纲量、e为边界符号、0为初始状态。

2.2 垂直裂缝井

当垂直裂缝井工作时,在地层中诱发平面二维椭圆渗流,即形成以裂缝端点为焦点的共轭等压椭圆和双曲线流线簇,如图1所示。

图1 垂直裂缝井直角坐标和椭圆坐标的关系示意图

直角坐标和椭圆坐标的关系为

式中:a,b分别为椭圆的长半轴、短半轴,m;L为裂缝半长,m。

从式(7)可得等压椭圆和双曲线流线簇:

用发展的矩形簇描述等压椭圆簇。用此方法得到的流量公式与Muskat[19]用复变函数方法得到的结果相同,表明此方法是正确的。

令垂直裂缝井流量为Q,则用椭圆坐标表示的渗流速度为

根据低渗透介质非线性渗流方程,可得低渗透介质中垂直裂缝井的椭圆非线性渗流流量为

2.3 分支水平井

当水平井工作时,在其周围地层中形成对称的共焦点的旋转等压椭球面和双曲面流线簇。令水平井的长度为2L′,井轴线位于直角坐标系的x轴上,如图2所示。

图2 水平井直角坐标和椭球坐标的关系示意图

直角坐标系和椭球坐标系的关系为

式中:a′,b′分别为椭球的长半轴、短半轴,m;L′为水平井半长,m。分支水平井如图3所示。

根据低渗透介质非线性渗流方程,可得低渗透介质中分支水平井的非线性渗流流量为

图3 分支水平井示意图

式(18)相当于达西渗流作用所产生的因子[20],而非线性渗流时增加了因子 Ωi。式中及图4中的QD,reD,ξeD,GD,n分别为无因次流量、无因次径向供给边界距离、无因次椭圆向供给边界距离、无因次起始水力梯度、井筒数。

令起始水力梯度为零,则非线性渗流流量公式(3)(13)(17)简化为相应的达西渗流的流量公式。

3 计算结果与讨论

图4 非线性渗流参数与供给边界对3种井渗流流量的影响

根据式(3)(13)(17),对低渗透介质中重直井、垂直裂缝井及分支水平井的非线性渗流流量进行计算,结果如图4所示。结果表明:①在其他条件相同时,起始水力梯度使得垂直井、垂直裂缝井及分支水平井流量降低。②在其他条件相同时,供给边界距离越大,垂直井、垂直裂缝井及分支水平井流量越小。③在其他条件相同时,垂直裂缝井的裂缝半长越大,流量越大。④在其他条件相同时,井筒数越多,分支水平井流量越大。

4 结 论

a.给出了低渗透介质中考虑起始水力梯度的垂直井、垂直裂缝井及分支水平井的非线性渗流流量公式。

b.在其他条件相同时,起始水力梯度使垂直井、垂直裂缝井及分支水平井流量降低;供给边界距离越大,垂直井、垂直裂缝井及分支水平井流量越小;垂直裂缝井的裂缝半长越大,流量越大;井筒数越多,分支水平井流量越大。

[1]朱陆明,吕艳斌,张舰,等.利用水平井法降低地下水位技术[J].浙江建筑,2005,22(5):46-47.

[2]刘慈群.单相和两相流体多维渗流问题[C]//周连第.第十届全国水动力学学术会议论文集.北京:海洋出版社,1996:439-445.

[3]陈崇希,万军伟.地下水水平井流的模型及数值模拟方法[J].地球科学:中国地质大学学报,2002,27(2):135-139.

[4]陈崇希.关于地下水开采引发地面沉降的思考[J].水文地质工程地质,2000(1):45-48.

[5]陈崇希,成建梅.关于滑坡防治中排水模式的思考:以长江三峡黄腊石滑坡为例[J].地球科学:中国地质大学学报,1998,23(6):628-630.

[6]HANTUSH M S,PAPADOPULOS I S.Flow of ground water to collector wells[J].J Hydraulics Division,1962,5:221-244.

[7]DAVIAU F,MOURONVAL G,BOURDAROT G,et al.Pressure analysis for horizontal wells[J].SPE Formation Evaluation,1987,3(4):716-724.

[8]CLEVELAND T G.Recovery performance for vertical and horizontalwells using semi-analytical simulation[J].Ground Water,1994,32(1):103-107.

[9]ZHAN Hong-bin.Analytical study of capture time toa horizontal well[J].J of Hydrol,1994,217:46-54.

[10]ZHAN Hong-bin,CAO Jiang.Analytical and semi-analytical solutions of horizontal well capture times under no-flow and constant head boundaries[J].Adv Water Resour,1994,23(8):835-848.

[11]TARSHISH M.Combined mathematical model of flow in an aquifer horizontal well system[J].Ground Water,1992,30(6):931-935.

[12]ZHAN Hong-bin,WANG Li-hong,PARK E.Onthe horizontal well pumping tests in anisotropic confined aquifers[J].J of Hydrol,1994,252(1/2/3/4):37-50.

[13]郭尚平,张盛宗,桓冠仁,等.渗流研究和应用的一些动态[C]//渗流力学进展.北京:石油工业出版社,1996:1-12.

[14]孔祥言,卢德唐.渗流力学的理论应用及其前沿研究[J].中国科技大学学报,2007,37(10):1262-1266.

[15]孔祥言.高等渗流力学[M].合肥:中国科技大学出版社,1999:1-7.

[16]邓英尔,刘慈群,黄润秋,等.高等渗流理论与方法[M].北京:科学出版社,2004:1-15.

[17]DENG Ying-er,LIU Ci-qun.Numerical simulation of unsteady flow through porous media with moving boundary[C]//ZHANG Feng-gan.Proceedings of the Third International Conference on Fluid Mechanics.Beijing:Beijing Institute of Technology Press,1998:759-765.

[18]DENG Ying-er,XIE He-ping,HUANG Run-qiu,et al.Law of nonlinear flow in saturated clays and radial consolidation[J].Applied Mathematics and Mechanics,2007,28(11):1427-1436.

[19]MUSKAT M.The flow of homogeneous fluids through porous media[M].New York:McGraw-Hill,1937.

Flow rates of nonlinear flows in low-permeability media for vertical well,vertically fractured well and branch horizontal

well

DENG Ying-er1,LIU Ci-qun2,ZHANG Wei1(1.State Key Laboratory of Geohazard Prevention and Geoenvironment Protection,Chengdu University of Technology,Chengdu610059,China;2.Institute of Porous Flow and Fluid Mechanics,Chinese Academy of Sciences,Langfang065000,China)

Formulas for the flow rates of nonlinear flows in low-permeability media for vertical well,vertically fractured well and branch horizontalwell considering the initial hydraulic gradients were presented.The influences of parameters for nonlinear flows(initial hydraulic gradient),supply boundaries,fracture length of vertically fractured well and wellbore number of branch horizontalwell on the flow rateswere analyzed.The results show thatwhen the other conditions are the same,the flow rates for the above three kinds of wells decrease because of the nonlinear flows.The flow rates are smaller when the supply boundaries are larger.The flow rate for the vertically fractured well increases when the fracture length is larger.The flow rate for the branch horizontal well increaseswhen the number of wellbores is larger.

nonlinear flow;vertical well;vertically fractured well;branch horizontal well;low-permeability medium;initial hydraulic gradient

TV139.14

A

1006-7647(2010)03-0017-03

10.3880/j.issn.1006-7647.2010.03.005

国家自然科学基金(40202036;40572163);四川省教育厅重点科技项目(07ZA009)

邓英尔(1967—),男,湖南邵阳人,教授,博士,从事水文地质、环境地质工程、岩土力学与渗流等研究。E-mail:dengye6789@sina.com

2009-06-01 编辑:骆超)