支持向量机分类误差不均衡内在原因分析

佛山市高明区广播电视大学 谢长菊

支持向量机分类误差不均衡内在原因分析

佛山市高明区广播电视大学 谢长菊

对于标准支持向量机C2SVM,样本数大小不同时,样本数量多的类别,其训练误差、预测误差小;而样本数量少的类别,其训练误差、预测误差反而大。这就导致分类类别误差的不均衡。就这一问题,对C2SVM在理论上进行分析,找出它们出现这种情况的内在本质的原因,指出了出现这种分类类别误差,是由C2SVM的本质、内在的特性决定的,并非由实验环境或者是算法实现过程中的偶然因素所致。

模式识别统计学习理论支持向量机

一、引言

统计学习理论[2]和支持向量分类机(SVM)正在成为继神经网络研究之后新的研究热点。SVM算法在模式识别、回归估计、概率密度函数估计等方面都有应用。特别是在模式识别方面,对于文本的自动分类、手写数字识别、语音识别、人脸图像识别等问题,SVM算法在精度上已经超过传统的学习算法。作为新生事物,SVM在实际应用中,不断出现一些新问题,等待我们去解决。比如正、负两类训练样本数目差别很大的时候,训练误差对于两类来说差别很大。这需要我们进行深入的研究。

二、雷达监测与分类误差率不均衡的问题

ChewHong2Gunn在文献[1]中,对SVM应用于雷达图像的目标自动监测进行了研究。对于低分辨率电子显像雷达图像的目标监测来说,大量的图像是不包含有目标的,而含有目标的图像所占比例非常小。如果以包含目标的样本图像作为正类,而不包含目标的图像作为负类,那么按照随机抽样原则获得的训练样本,正类样本数目很少,而负类样本占有绝对多数的比例。这就出现了不同类别之间,训练样本数目上不均衡的情况。作为训练集来说,样本数目在各个类别之间不均衡是很正常的。在实际应用中,我们也没有理由要求所获得的训练样本,在不同类别中的数目都相同。那么这种不均衡对SVM的训练效果有没有影响,有什么样的影响,如何消除这种影响?对于这个问题,结合实验,文献[1]针对C2SVM在理论上作了如下粗略的分析。指出如果l-、l+分表示是正、负类训练样本数,那么分类错误率之比为:

如此说来,对于标准支持向量机C2SVM,样本数大小不同时,样本数量多的类别,其训练误差、预测误差小,而样本数量少的类别,其训练误差、预测误差反而大。这就是类别误差不均衡。这样的类别误差不均衡,在很多场合必须给予消除和调整。对于雷达目标监测问题来说,宁愿出现误报警(不应该报警却报警了),也不愿出现漏报警的情况(应该报警却没有报警)。类似情形出现在疾病诊断、故障分析中。

三、SVM分类误差率不均衡内在原因分析

提高SVM分类能力,是SVM研究的根本目的。SVM出现类别分类误差不均衡的问题,必须进行调整,即类别补偿。但是在考虑如何进行类别补偿之前,首先需要思考:出现这种分类类别误差,是由SVM的本质、内在的特性决定的,还是由实验环境或者是算法实现过程中的偶然因素所致,不均衡是否是SVM内在的规律?导致SVM训练误差和预测误差不均衡的内在原因是什么?现在针对标准支持向量机C2SVM进行分析。首先来考虑C2SVM的原始问题:

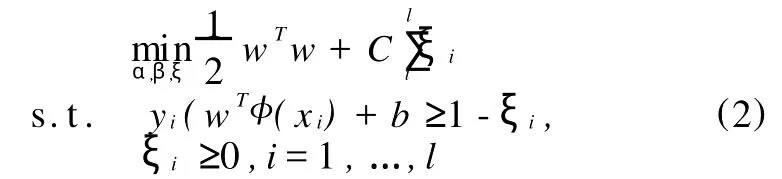
对应的拉格朗日函数为:

若α为它的对偶问题的最优解,则其应该满足如下的KKT条件:

所谓的边界支持向量,就是ξi>0所对应的向量。此时,由KKT条件(4)知,α1=C。满足这样条件的向量记为BSV,它们是错误分类的样本。用NBSV+、NBSV2分别为正、负类边界支持向量的数目,则有:

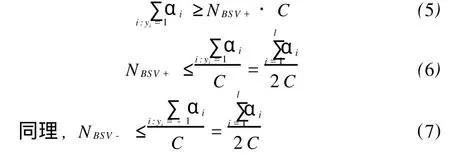
这就是我们要找的结论:无论正类、负类样本数差别多大,C2SVM给NBSV+和NBSV2所提供的上界都是相同的。如果考虑的不是分类错误的数目,而是分类错误的比率,当正类、负类样本数相差很大时,就会必然导致分类误差的不均衡。这就是SVM分类误差率不均衡的内在原因。

四、小结

对于标准支持向量机C2SVM,样本数大小不同时,样本数量多的类别,其训练误差、预测误差小;而样本数量少的类别,其训练误差、预测误差反而大。这就是分类类别误差的不均衡。

通过理论分析发现,出现这种分类类别误差,是由C2SVM的本质、内在的特性决定的,而非由实验环境或者是算法实现过程中的偶然因素所致。

[1]Chew Hong2Gunn ,Crisp D.J .,Bogner R.E.et al.Target detection in radar imagery using support vector machines with training size biasing [ A ].In : Proceedings of the sixth international conference on control , Automation ,Robotics and Vision[C],Singapore ,2000

[2]Vapnik V., The nature of statistical learning theo2ry.Springer2Verlag , New York.NY, 1995 ,张学工译,统计学习理论的本质,清华大学出版社,2000

[3]Vapnik V , Statistical learning theory [ M].NewYork.John Wiley >Sons , 1998

[4]Scholkopf B., Smola A., Williamson R.C.et al ,New support vector algorithms[J ].Neural Compu2 tation , 2000 , 12 (5) : 120721245

book=110,ebook=64