受承台和埋深影响的沉井水平位移计算
2010-09-05殷永高孙敦华周正明中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室武汉43007安徽省高速公路总公司合肥3005
刘 鹏,殷永高,孙敦华,周正明(.中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室,武汉 43007;.安徽省高速公路总公司,合肥 3005)
受承台和埋深影响的沉井水平位移计算
刘 鹏1,殷永高2,孙敦华2,周正明1
(1.中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室,武汉 430071;2.安徽省高速公路总公司,合肥 230051)
在桩的线弹性地基反力法基础上,求出考虑承台以及埋深影响的沉井水平位移的通解,即在沉井计算中,经常遇到的地面处水平抗力不为0时新的计算方法。并对沉井的边界条件作出了数学上的归纳总结,它们涵盖了在实际中可能遇到的大多数情况。推导出了对应于每种工况的显式表达式,并利用安徽马鞍山长江大桥的实际数据验证了所求得的显式解的数学上的正确性和力学上的合理性。所得出的公式对长桩、短桩、细桩、粗桩以及沉井桩都适用。承台对沉井(桩)的约束体现在桩顶的边界条件中。
弹性解;桩;沉井;承台
1 概 述
根据Poulos和Davis[1]研究,桩水平方向上的最大偏移是设计的关键所在。目前国际上通用的计算方法主要分为3类[2]:
第1种方法是单桩的弹性解法,这种方法在分析土和桩之间的相互作用时,使用“地基反力”这个概念[3]。土的反力和桩变形的比值被称为土的水平反力系数Es。我们已经有了当Es随深度变化为常数的解[3],当Es随深度线性变化的解[4],和Es随深度非线性变化的解[5]。
第2种方法是非线性Py法[6],当土变形较大时,将会呈现非线性。因此,在不同深度下如何获取Py曲线就成了关键所在。我们一般通过试验或解方程组的办法来获得。Matlock[7]提出了软黏土的Py曲线计算方法,Reese[8]提出了硬黏土的Py曲线计算方法,Cox和Reese[9]提出获得Py曲线的试验方法。Py曲线法的优点在于它能适用于很广泛的土的类型和真实的加载条件,得到的结果与实际也吻合得较好,充分考虑了土的非线性。缺点在于Py曲线法把土分割成一个个离散的单元,并且把土压力转化成了节点荷载;另一个不足是在实际应用中计算的输入输出费时费力。在实际工程中,我们需要一种更简单实用的方法。
第3种方法是由Evans和Ducan提出的特征荷载法(CLM)[10],这种方法和非线性Py法的结果相近,但计算速度更快。但在对CLM法的计算结果使用上,我们必须十分小心,通常在用CLM法求位移时,最好先有一组在所求地层条件下的现场实测值与CLM法计算所得结果作对比,证明方法和所取参数可行,再推广应用。
在实际工程中,桩的线弹性地基反力法因为其简单容易计算的特点,在技术人员的设计与评估中仍有广泛的应用。只要参数选取合理,此法有较好的精度。本文在借鉴桩的线弹性地基反力法的基础上,考虑地面处水平抗力不为0,求出了适合于沉井应用的修正解法。并将受承台约束沉井的边界条件归纳成3种,推导出了其表达式。
2 桩(沉井)的挠曲微分方程[11]
设置于土中的竖向弹性桩,地面处承受横向荷载(水平力H0和弯矩M0),因此,桩顶产生横向(侧向)位移y0和转角φ0(桩身受有水平分布荷载珋q(z)作用)。由于荷载作用,桩将发生挠曲,支撑桩的弹性介质(土)将产生连续分布的土反力。假定桩上任意一点z处单位桩长上的反力珋p=珋p(z,y)。若忽略由于桩挠曲引起的竖向摩擦力,则各截面仅有水平向地基土反力。
现截取桩身的一个微分单元,单元两侧分别作用分布荷载珋q(z)和土反力珋p(z,y),上截面作用剪力Q(与y轴同向)和正弯矩M(顺时针向),下截面作用负剪力Q+d Q和负弯矩M+d M(见图1)。由单元体上水平力之和为0的平衡条件可推得
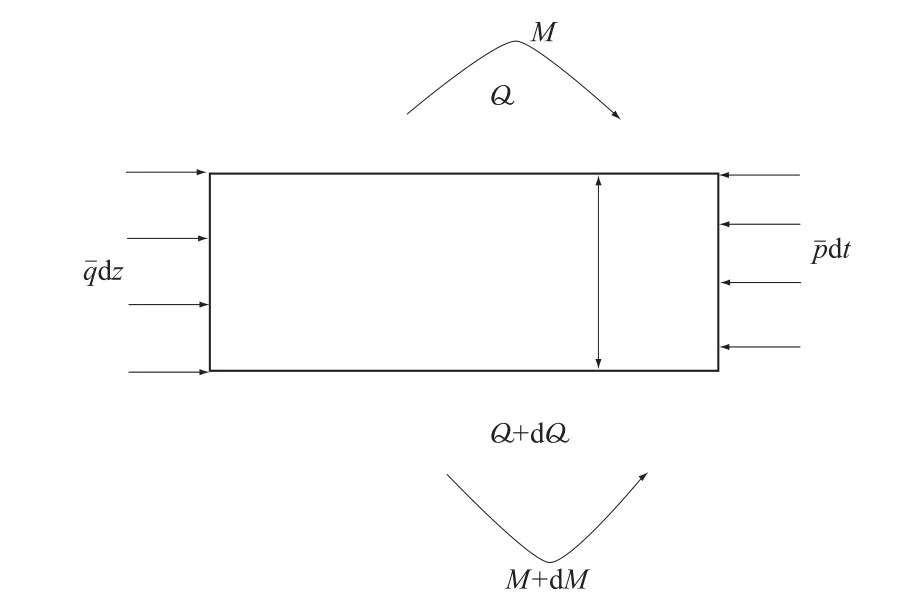
图1 设置于土中的弹性桩Fig.1 Elastic pile in soil
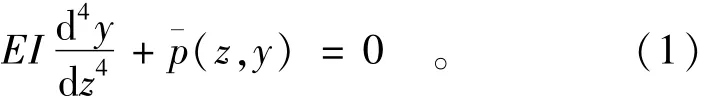
这就是结构物基础主动桩(沉井)的基本挠曲微分方程。
3 土水平反力系数修正表达式
设置于弹性介质中的弹性桩,假定桩侧地基土为线弹性体,这里采用常用的线弹性地基反力法。假定桩侧土为温克尔(Winkler)离散线形弹簧,不考虑桩土之间的粘着力和摩阻力,任一深度z处,桩侧土反力与该点水平位移y成正比,表示为
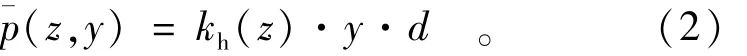
式中,地基土水平反力系数kh(z)随深度变化的表达式有不同的假定[12]。在本文中,我们假设地基土反力系数随深度呈线形增长,变化趋势与m法相似,但是在地表处k的值不为0,即在一个常数基础上的线性增加,表达式为:kh(z)=k(z+c0),k为比例系数;c0为地表处的kh/k的值,也可以看作是埋深;z为深度。公式改写为
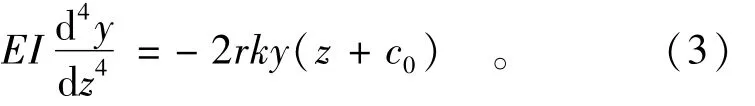
式中:2r为桩的宽度,r为桩的半径;E为桩的弹性模量;I为桩截面惯性矩;EI为抗弯刚度。
这种土反力系数的形式,考虑了土的粘聚力和埋深的影响。在桩基计算中,对c0的处理一般是忽略。但在本文所基于的马鞍山长江大桥中,沉井的直径尺寸远大于一般的桩,且由于工地表层土为软黏土,所以在实际计算中需要单独考虑,以便满足实际的需要,也为了反映出它的影响。
4 桩(沉井)挠曲微分方程的求解
采用幂级数法求解偏微分方程(3),设
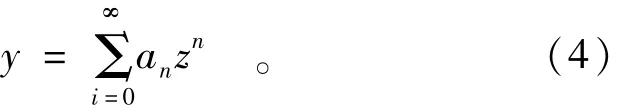
把方程(4)代入方程(3),由对应项系数相等和边界条件,可得:

所以,式(8)可以写成


因式(6)可以写成
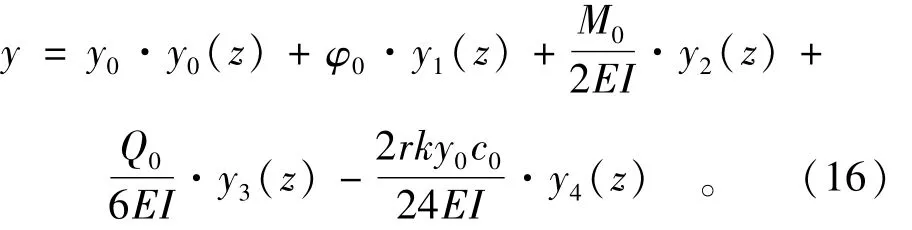
亦可以改写为
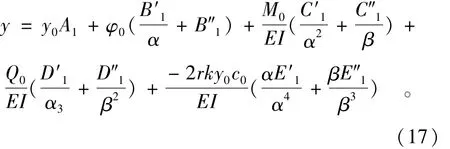

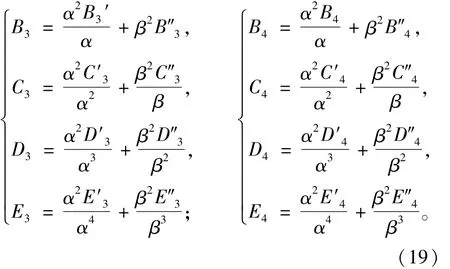
对(17)式所求的导数可以写成A1,B′1,C′1,D′1,E′1,……A4,B″4,C″4,D″4,E″4的值,在沉井情况下,可以事先算出,用的时候直接查表即可。求参数的时候,要使用换算深度h′=αz,h″=βz。
根据参数表列出的参数,我们可以通过公式计算出我们所需要的参数值,然后代入公式(18)就可以用来求我们需要的位移和力。
5 三组边界条件的显式解
在考虑承台的约束作用和埋深的影响的基础上,本文结合在实际计算中遇到的考虑承台约束的沉井的边界条件,归纳成了3种,推导出了其显式表达式,以便于应用。
工况1:沉井的底部立于岩石中,或沉井的长度足够长,底部转角比较小,承台的转角φ0范围可以估测时,得


上面所提到的的3种,是在实际计算中经常使用的。对于其它工况,只要从本文推导的公式出发,可以一一求出。
6 工程实例
我们利用求出的显式表达式,来计算安徽马鞍山长江大桥锚碇的水平向位移。表1为沉井的几何尺寸,表2为此种工况下的计算模型参数。

表1 沉井和锚碇的几何尺寸Table 1 The geometry size of the caisson and anchorages

表2 计算模型参数Table 2 Themodel parameters of calculation
算例1:当沉井受到30 000 t水平力,由于承台的作用,井顶转角为0.2°,在综合考虑承台的约束作用和桩的几何参数后,我们选用第2组条件的显式解,在这里我们取M1和φ1近似为0。图2为计算出来的桩长取35 m时所对应的水平向位移关系曲线。
算例2:在受到与算例1相同的水平力,同样几何尺寸的沉井长度为48 m,井顶转角为0.05°,0.1°,0.15°时,图3为计算得到的各条水平向位移关系曲线。
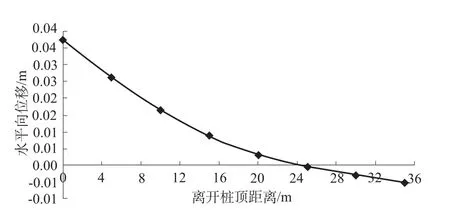
图2 桩长为35 m时沉井轴向的水平向位移关系曲线Fig.2 Axial horizontal displacement curve of the caisson w ith 35meterlong pile
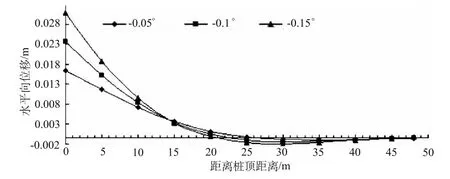
图3 48 m桩长沉井轴向水平位移曲线Fig.3 Axial horizontal displacement curves of the caisson w ith 48meterlong pile
算例3:在受到与算例1、算例2相同的水平力,同样几何尺寸的沉井,井顶转角为0.2°,长度为48 m,埋深为5m时(C0=5 m),图4为计算出的水平向位移关系曲线。
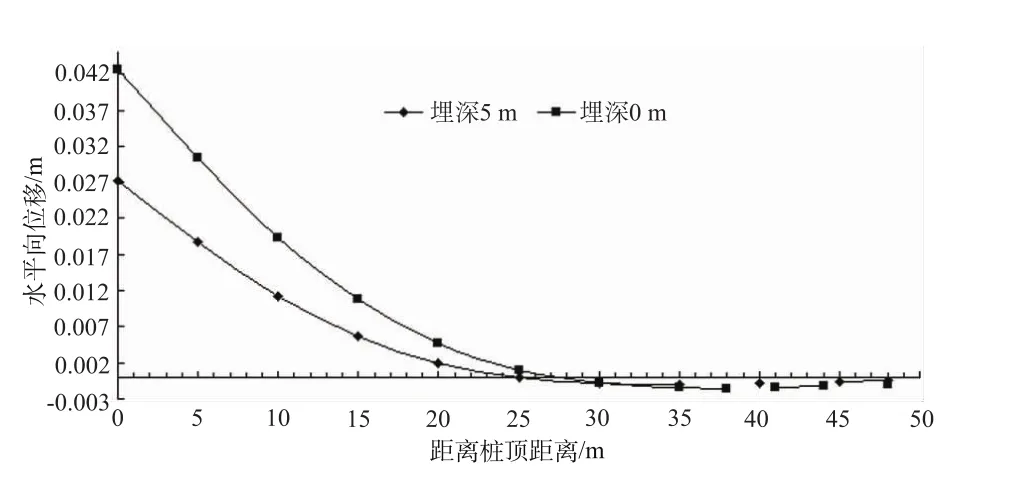
图4 不同埋深沉井轴向水平位移曲线Fig.4 Axial horizontal displacement curves w ith different dep ths
由图4,我们可以清楚的看出当沉井埋深取不同值时,沉井的水平井顶位移有较大变化,埋深为5 m时的水平向位移比埋深为0 m的水平向位移小了60%以上。
7 结 论
本文推导的简化理论计算公式,考虑了承台埋深的影响,给出了常用边界条下的显式解。公式简单,便于设计咨询业界应用。所得出的公式对长桩、短桩、细桩、粗桩以及沉井桩都适用。计算得出了与理论预测相符的变形曲线,计算结果也有很好的精度。
[1] POULOS H G,DAVIS E H.Pile Foundation Analysis and Design[M].New York:Wiley,1980.
[2] CHEN YungTsang.Lateral load analysis of single piles[M].Davis:University of California,2004.
[3] HETENYI M.Beams on Elastic Foundations:theory with applications in the fields of civil and mechanical engineering[M].Ann Arbor:The University of Michigan Press,1946.
[4] REESE L C,MATLOCK H.Nondimensional solutions for laterally loaded piles with soilmodulus assumed proportional to depth[C]∥Proceedings Eighth Texas Conference on Soil Mechanics and Foundation Engineering Special Publication No.29.Austin:University of Texas,1956.
[5] MATLOCK H,REESE L C.Generalized solutions for laterally loaded piles[J].Journal of Soil Mechanics and Foundation Division,ASCE,1960,86(5):63-91.
[6] McClelland and Focht.Soilmodulus for laterally loaded piles[J].Transactions,ASCE,1958,123:1071-1074.
[7] Matlock,H.Correlations for design of laterally loaded piles in soft clay[C]∥Proceedings,2nd Annual Offshore Technology Conference.Houston:1970.
[8] REESE L C,WELCH R C.Lateral loading of deep foundations in stiff clay[J].Journal of the Geotechnical Engineering Division,ASCE,1975,101(7):633-649.
[9] REESE L C,COXW R,KOOP F D.Analysis of laterally loaded Pples in sand[C]∥Proceedings,5th Annual Offshore Technology Conference.Houston:1974.
[10]DUNCAN JM,EVANS Jr LT,OOIPSK.Lateral load analysis of single piles and drilled shafts[J].Journal of Geotechnical Engineering.ASCE,1994,120(5):1018-1033.
[11]左名麟,胡人礼,毛洪渊.桩基础工程[M].北京:中国铁道出版社,l996.(ZUO Minglin,HU Renli,MAO Hongyuan.Pile Foundation Engineering[M].Beijing:China Railway Press,1996.(in Chinese))
[12]刘金砺.桩基基础设计与计算[M].北京:中国建筑工业出版社,l991.(LIU Jinli.Pile foundation design and calculation[M].Beijing:China Building Industry Press,1991.(in Chinese) )
(编辑:赵卫兵)
Horizontal Displacement of Single Pile Constrained by Buried Platform
LIU Peng1,YIN Yonggao2,SUN Dunhua2,ZHOU Zhengming1
(1.State Key Laboratory of Geomechanics and Geotechnical Engineering,Institute of Rock and Soil Mechanical,Chinese Academy of Sciences,Wuhan 430071,China;2.Anhui Expressway Holding Group Co.,Ltd,Hefei 230051,China)
A general elastic solution for single pile constrained by buried platform was derived to calculate the horizontal displacement,the shear stress and the bendingmomentof the pile.The specially explicit solutions for several boundary condition groupswhich aremerged into three group scenarios are presented.Three examples are presented to highlight themathematical correctness and themechanical rationality of the obtained solutions.The solutions are applicable to both short and long piles and even caissons.
elastic solution;pile;caisson;platform
TU411.3
A
1001-5485(2010)07-0041-06
20090926;
20100105
刘 鹏(1985),男,山东青岛人,硕士,主要从事工程力学及计算土力学研究,(电话)13100621398(电子信箱)liupengreal@sina.com。
