基于灰色系统理论的几种需水量预测方法分析
2010-09-05李洪伟廖城毅西南大学资源环境学院重庆400716
杜 涛,叶 琰,李洪伟,廖城毅,沈 亮(西南大学资源环境学院,重庆 400716)
基于灰色系统理论的几种需水量预测方法分析
杜 涛,叶 琰,李洪伟,廖城毅,沈 亮
(西南大学资源环境学院,重庆 400716)
在灰色系统理论下,运用几种方法弱化原始需水量数据,并进行对比分析。分析表明二阶弱化算子修正与累加生成相结合的方法精度较高,最终验证了该模型应用于重庆市北碚区需水量预测的可行性及有效性,预测2015年北碚区需水量为2.45亿m3,2020年北碚区需水量为2.69亿m3。
灰色模型;二阶弱化算子修正;需水量预测;精度
随着经济的飞速发展以及与日俱增的人口对水的需求越来越多,水资源的供需矛盾愈益突出。加之水资源的不合理利用造成的浪费,使得我国面临的水资源危机越趋严重,同时给社会经济带来负面影响十分巨大,严重制约了城市经济的发展,影响人民的生活水平。水资源的短缺已成为我国经济发展的重要制约因素,供水管理向需水管理转变也就成为必然。科学合理地对城市供需水量进行全面有效的预测分析,实现水资源优化配置,可以为城市水资源合理有效地使用以及社会经济的发展提供保障,具有重大的意义。
1 灰色系统理论
灰色系统理论在我国于1982年由著名学者邓聚龙教授提出,经过近30年的发展完善,它的科学思想和研究方法已经渗透到了许多科学领域,它所使用的灰色数学方法已广泛应用于工程系统、经济系统、农业系统、气象系统、生态系统、社会系统、未来学研究等科研工作中[1-3]。
所谓的灰色系统理论就是指既含有已知信息,同时又含有未知的或非确定的信息系统,其属于黑箱概念的一种推广,是黑色与白色相结合的一种系统理论。利用已知的白化参数通过分析、原始数据误差弱化、建模、精度评定、控制和优化等程序,将灰色问题淡化和白化,在允许误差精度范围内,达到未知信息已知化。尽管客观系统表象复杂,信息不充分,但主脉必是有整体功能的,且是有序的,在离散的数据中必然蕴含着某种内在的规律可循,该系统理论提出了一种利用微分方程建立数学模型的思想,将原始的数据通过一系列的数学方法进行处理,将其转化为微分方程来描述系统的客观规律。通过对所得微分方程描述的事物理论规律与现实规律进行精度评定,以判断所建模型是否合适,从而进一步实施未知信息的白化过程。
2 灰色建模
2.1 灰色生成
预测即人们对客观事物发展变化过程的一种认识与估计。通常使用的预测模型是因子模型,因子模型建立的关键是要找出与预测对象相关性好而因子之间又彼此独立的预报因子,并且建立前期预报因子与后期预报量之间的某种联系,然后按照这种规律作预测[4]。然而由于事物的发展变化过程复杂多样,各种变量因子之间相互联系、影响、制约,要想建立因子模型是十分困难的,引进灰色系统理论预测模型则为事物的发展变化预测提供了新的方法理论。GM(1,1)预测模型克服了变量之间的相互影响,只要将GM(1,1)模型与不同的数据生成处理相结合,即可达到不同的预测目的。
模型的建立要先对所得的数据进行初步处理,把无明显规律的时间系列,经过初步处理后(本文拟采用了三种方法进行处理,分别为原始数据累加、滑动平均法弱化后进行数据累加,以及二阶弱化算子法弱化后进行数据累加)使之生成有明显规律的时间系列,然后利用灰色系统理论结合初步处理数据建立GM(1,1)预测模型,进行需水预测。
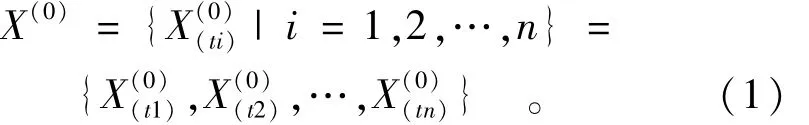
由于该模型实质上是一个指数型函数,其预测效果很大程度上取决于原始数据的特点,要求时间序列近似服从指数规律变化或者说要求数据总体上呈单调较平缓变化,而不是周期性或无序性变化。如果由初步获得的原始数据判断,并不完全符合模型的要求,那么,要对于原始数据做初步的处理以期得到随机性弱化、规律性强的新数列,该过程称为灰色生成。一般的应用方法有累加生成、累减生成、均值生成和归一化生成等。
本文采用了3种方法(①累加生成法[5],②滑动平均法[6,7]与累加生成相结合,③二阶弱化算子修正[8-10]与累加生成相结合)对原始数据进行弱化,并通过每次所得结果,寻找进一步优化的方法,以期达到更加合理的效果。
2.1.1 单纯累加生成

2.1.2 滑动平均法与累加生成相结合

2.1.3 二阶弱化算子修正与累加生成相结合
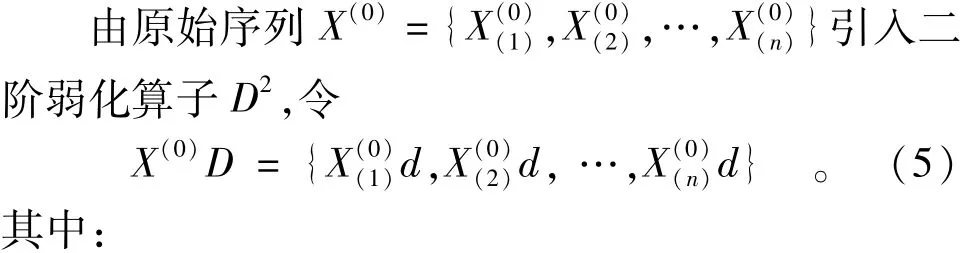
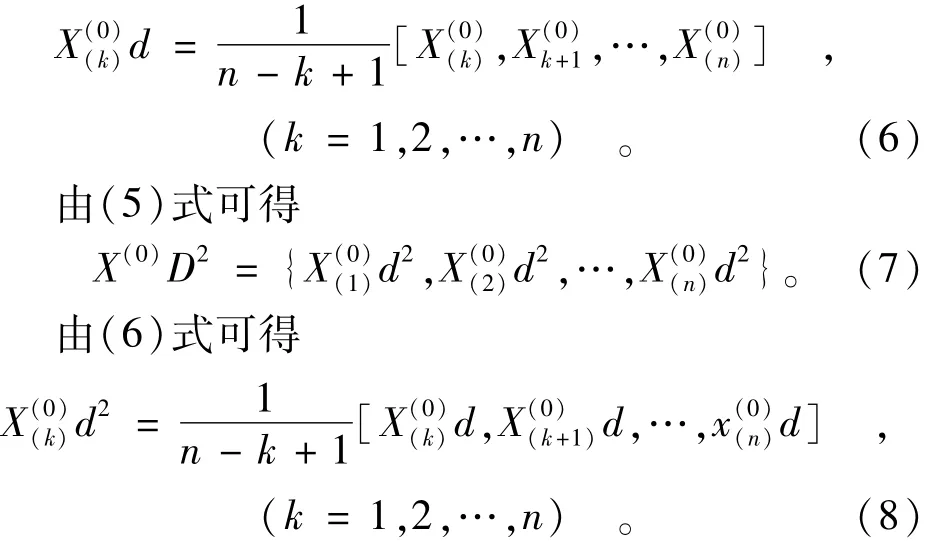
以上经二阶弱化算子得到的X(0)D2再经依次累加生成即得到。
2.2 模型建立
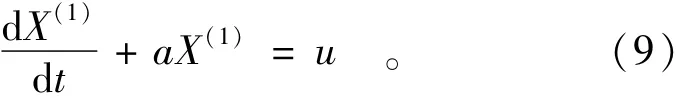
其中的a,u为对应的白化参数,2参数的具体确定方法可由最小二乘法近似求得。将上式按导数形式变换并写成矩阵形式为
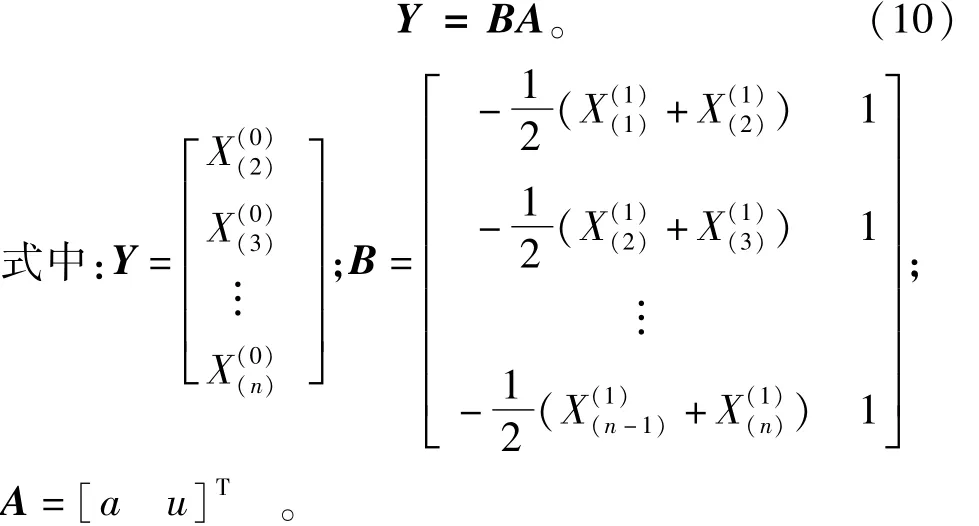
经上面计算处理可以确定Y与B均为已知,因此由式(10)可以求得两参数a,u的值,为进一步简化计算过程可写成如下形式:
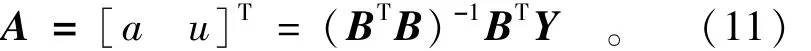
上式求解过程可以Matlab7.0软件[11]编程求得a,u值,或者可以用Excel中的mmult(矩阵相乘)和minverse(矩阵求逆)函数结合求得,当数据较少时可采用后者逐一输入,但当数据较多时建议采用前者可以减少工作量。
最后,再将求得的参数值重新代入原白化微分方程即可得出预测模型方程,基本形式为
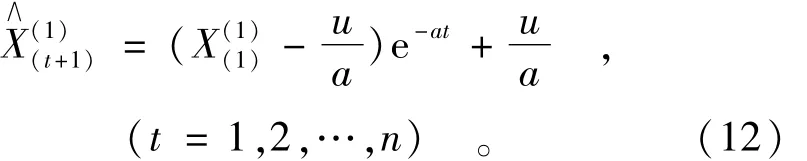
以上得出的预测模型计算结果为预测累加值,进一步累减后方可得到还原值:
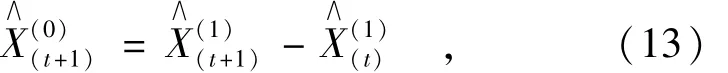
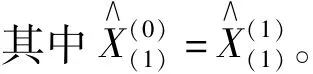
3 误差检验
对于一个模型是否符合要求,要经过多方面的检验判断,只有各方面的检验均能通过的模型才能用于预测。一般灰色预测模型的精度评定通过利用后验差方法,对残差分布的统计特性进行检验,但为了安全可靠,本文对于所得灰色预测模型进行全面的检验,以确保其符合要求。
以下采用残差大小检验[12]、后验差检验[13,14](后验差比值C和小误差概率检验P)判断模型的精度:

(3)相对误差大小ε对于给定的a>0,当ε<a时,所得模型为残差合格模型。相应的精度检验等级参照表见表1。
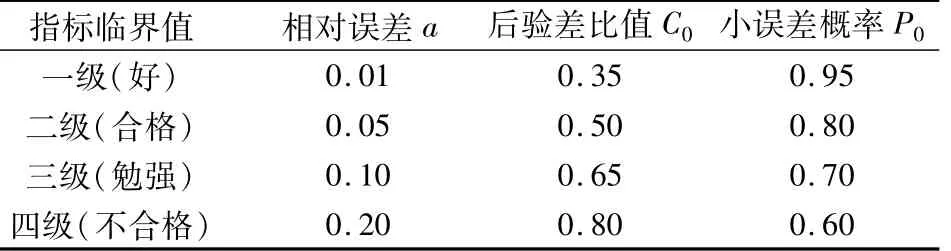
表1 精度检验等级参照表[6,8,15]Table 1 Accuracy exam ination level
4 实例分析
将以上理论应用于重庆市北碚区。首先对原始数据序列依照3种方法进行初步弱化,最终得到累加值序列。详细计算结果见表2、表3、表4。
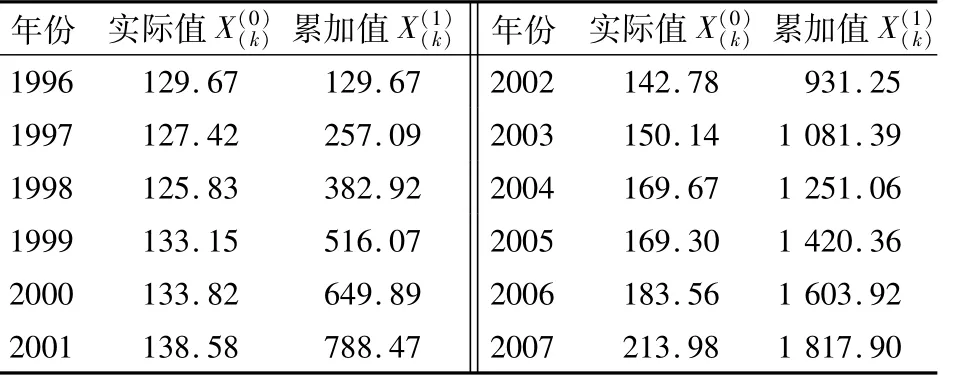
表2 原始数据及累加结果Table 2 The array of original data and cumulative data 106m3
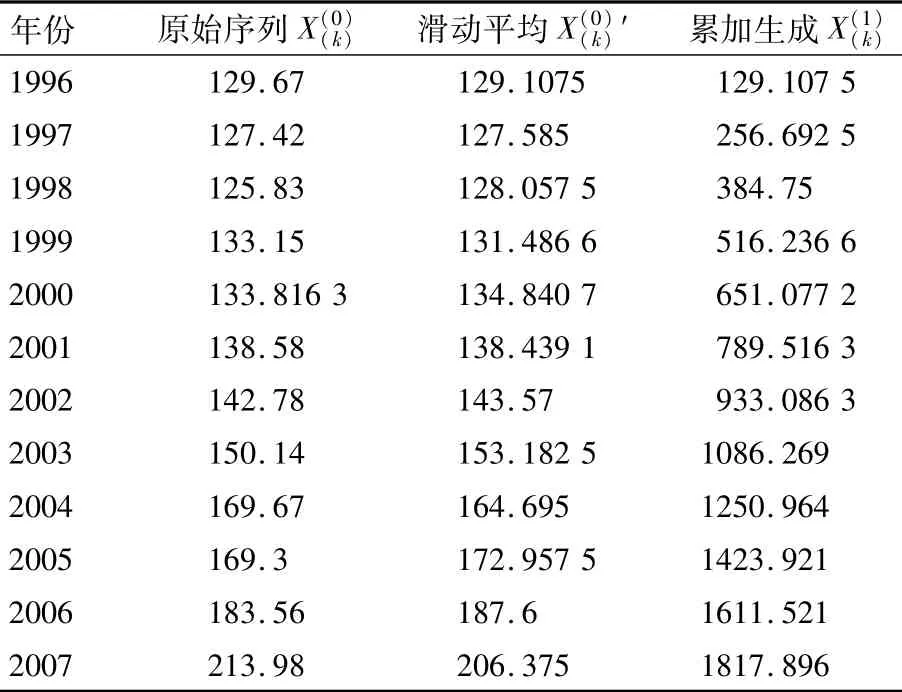
表3 滑动平均后累加生成序列Table 3 Generation sequence of data after combining average and cumulative 106m3
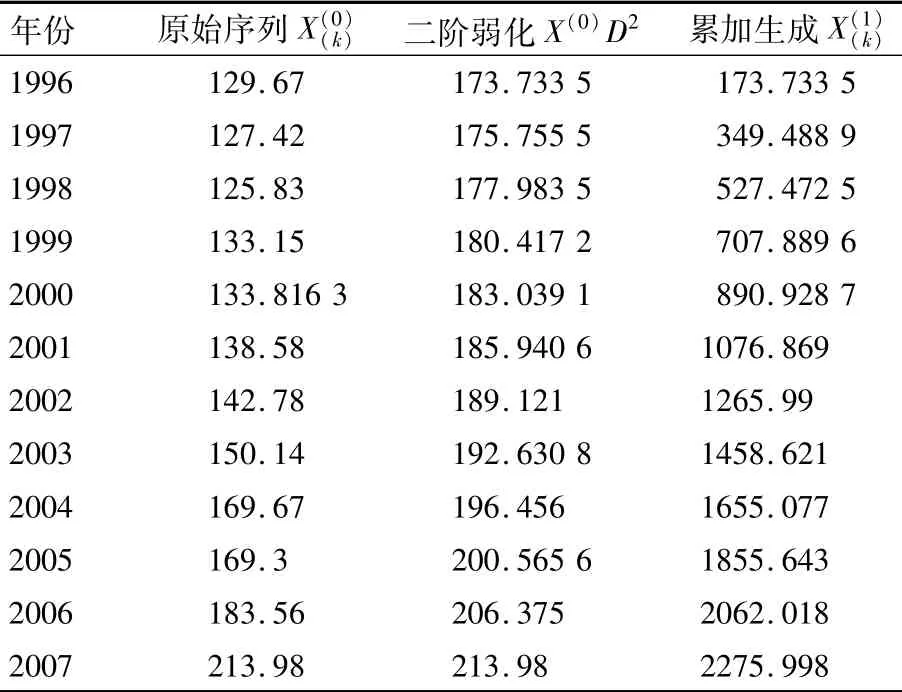
表4 二阶弱化后累加生成序列Table 4 Generation sequence of data after combining twoorder weakening and cumulative 106m3
由处理后的数据序列求解预测模型,依照上述原理可分别做出3种方法所对应的重庆市北碚区年需水量预测结果(表5),同时计算各预测方法的残差ε(0)及残差百分比,,
对比各种方法预测结果误差的大小以确定最终选用的灰色预测模型。
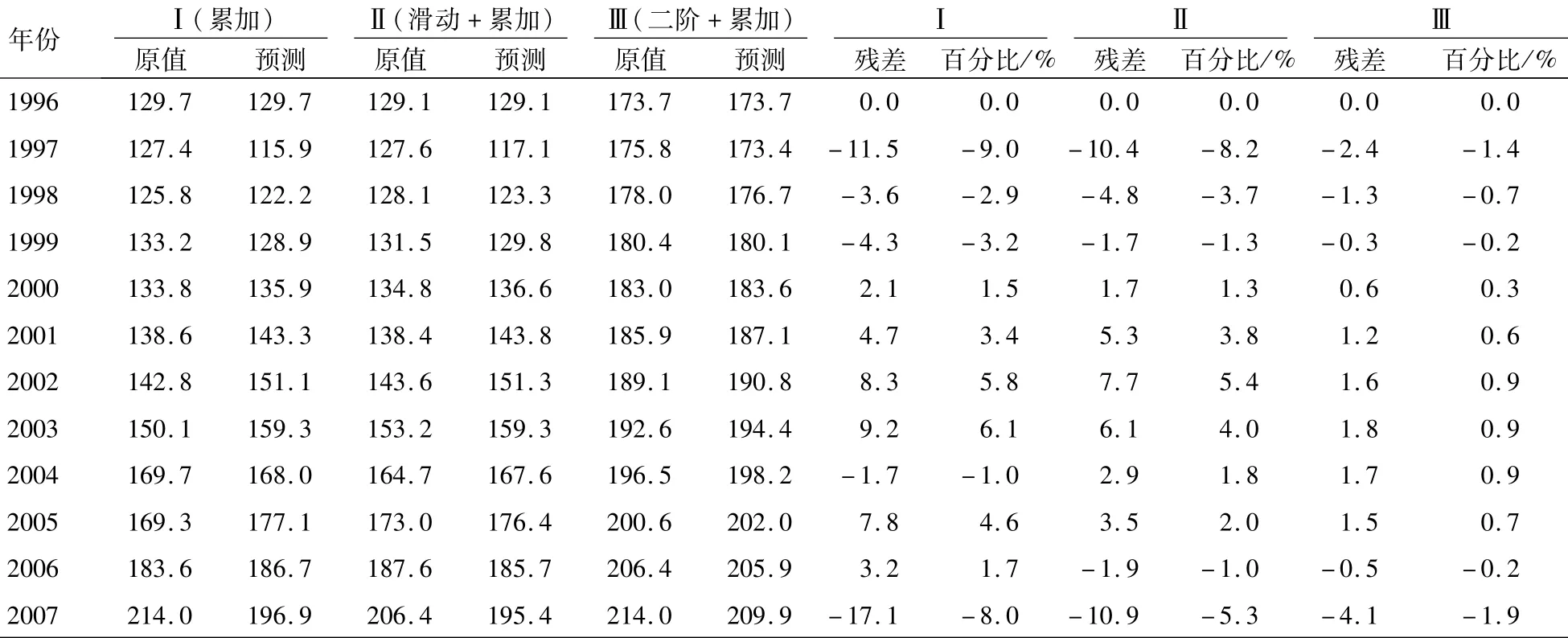
表5 3种预测方法结果对照表Table 5 Comparison among the threemethods
对比表5结果可以明显地发现:单纯的累加生成所得的预测模型预测结果误差较大,先经过滑动平均处理后再进行累加生成,所得到的预测结果较前一种方法来看误差方面较为合理一些,但两者都比第3种方法所得的预测结果误差要大。而且,1997年与2007年2年的误差为所选取序列中误差最大的2年。这是因为1997年是由于重庆成为直辖后,部分统计口径发生变化;2007年重庆发生特大洪涝灾害,且在2006年发生了特大干旱。这从侧面也验证了模型预测的精度。
对以上3种预测模型进行精度评定:

经比较,3种方法中前2种的相对误差项属于二级合格标准,另外两项属于一级好的标准;而第3种方法3项均符合一级标准,由此可得知选择第3个预测模型完全符合预测要求,可将其应用于具体预测实践当中。因此,选定第3种方法做为预测模型。其对应的白化参数值以及灰色模型如下:
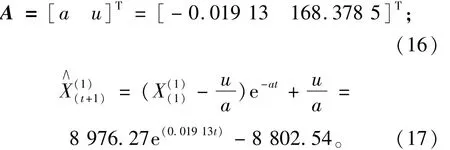
运用二阶弱化算子修正与累加生成相结合的灰色预测模型,预测重庆市北碚区2010年、2015年、2020年的年需水量分别为222.3×106,244.6×106,269.2×106m3。
5 结 论
灰色模型为指数模型,对原始数据的特点依赖性较大,因此模型的精度也很大程度上取决对原始数据的初步处理以及弱化方法。本文通过选取3种弱化原始数据的方法,对3种方法预测结果进行对比并最终经过精度评定来确定符合要求的预测模型。运用二阶弱化算子修正与累加生成相结合的灰色预测模型对于城乡水资源的供需预测,以期达到供需平衡,具有现实意义。
[1] 马兴冠,马志孝,崔伟,等.灰色神经网络耦合模型在城市需水量预测中的应用[J].沈阳建筑大学学报,2008,24(4):653-657.(MA Xingguan,MA Zhixiao,CUIWei,et al.Prediction of urban water demand with couple model method[J].Journal of Shenyang Jianzhu University Natural Science,2008,24(4):653-657.(in Chinese))
[2] 王好芳,董增川.区域经济人口系统需水量的灰色预测方法研究[J].西北水资源与水工程,2001,12(2):53-54.(WANG Haofang,DONG Zengchuan.Water demand on system of regional economy and population[J].NorthwestWater Resources and Water Engineering,2001,12(2):53-54.(in Chinese))
[3] 刘晓霞.城市需水量预测的思路和方法探讨[J].山西水利,2004,38(1):38-39.(LIU Xiaoxia.Ideas and methods of urban water demand forecasting[J].Shanxi Water Resources,2004,38(1):38-39.(in Chinese))
[4] 李祚泳.灰色系统理论及其应用进展[J].自然杂志,1988,12(7):483-488.(LIZuoyong.Progress on grey system theory and its application[J].Nature Magazine,1988,12(7):483-488.(in Chinese))
[5] 刘二敏,杨侃.灰色系统理论改进技术在城市生活需水预测中的应用[J].黑龙江水专学报,2007,34(1):19-21.(LIU Ermin,YANG Kan.Innovate technologically grey system theory in city lifewater demand forecasting[J].Journal of Heilongjiang Hydraulic Engineering College,2007,34(1):19-21.(in Chinese))
[6] 魏令勇,白润才.城市用水量预测模型及其应用[J].辽宁工程技术大学学报,2005,24(S1):288-289.(WEILingyong,BAIRuncai.Model to appraise water requirementof city and its application[J].Journal of Liaoning Technical University(Natural Science Edition),2005,24(S1):288-289.(in Chinese))
[7] 于书霞,尚金城.城市水资源供需系统优化分析[J].自然资源学报,2002,17(2):229-233.(YU Shuxia,SHANG Jincheng.Optimization of the supply and demand system of urban water resources[J].Journal of Natural Resources,2002,17(2):229-233.(in Chinese))
[8] 马文敏,唐莲.灰色系统理论在城市需水量预测中的应用[J].西北水资源与水工程,2001,12(1):14-16.(MAWenmin,TANG Lian.An application ofgreymodel in forecasting city water[J].Northwest Water Resources and Water Engineering,2001,12(1):14-16.(in Chinese))
[9] ZHAO Xinhua,TIAN Yimei,CHEN Chunfang.Research on municipal water demands forecast[J].Transactions of Tianjin University,2001,7(1):21-25.
[10]胡德秀,杨杰.城市需水量的灰色非线性预测[J].陕西水力发电,1999,15(1):23-27.(HU Dexiu,YANG Jie.Grey nonlinear forecasting of metropolis water demand[J].Journal of ShanXiWater Power,1999,15(1):23-27.(in Chinese))
[11]张瑞丰.精通MATLAB6.5[M].北京:中国水利水电出版社,2004.(ZHANG Ruifeng.Proficient in Matlab6.5[M].Beijing:China Water Power Press,2004.(in Chinese))
[12]席 洋,程水源,郭秀锐,等.灰色预测模型在城市需水量预测中的应用[J].环保科技,2007,13(1):25-34.(XIYang,CHENG Shuiyuan,GUO Xiurui,et al.An Application of greymodel on urban city water demand forecasting[J].Environment Protection and Technology,2007,13(1):25-34.(in Chinese))
[13]TSENG Fangmei,YU Hsiaocheng,TZENG G.Applied hybrid grey model to forecast seasonal time series[J].Technological Forecasting and Social Change,2001:291-302
[14]张雅君,刘全胜.城市需水量灰色预测的探讨[J].中国给水排水,2002,18(3):81.(ZHANG Yajun,LIU Quansheng.An investigation of greymodel on city water demand[J].ChinaWater and Wastewater,2002,18(3):81.(in Chinese))
[15]TSENG FM,TZENGG H,YU CH,etal.The comparison of four kinds of prediction methods:ARIMA,Fuzzy Time Series,Fuzzy Regression Time Series and Grey Forecastingan example of the production value forecast of machinery industry in Taiwan[C]∥1997 Second National Conference on Grey Theory and Applications,Taibei.1997:53-68.
(编辑:王 慰)
Analysis of SeveralW ater Demand Prediction M ethods Based on Gray System Theory
DU Tao,YE Yan,LIHongwei,LIAO Chengyi,SHEN Liang
(College of Natural Resources and Environment,Southwest University,Chongqing 400716,China)
On the basis of the gray system theory,we weaken the original data of water demand by using several methods,then conduct comparative analysis on forecasting results.Analysis shows that the result obtained from the combination of secondorder weakening operator with the AGO can get the highest accuracy.Finally,we validate the feasibility and effectiveness of the model which is applied to forecasting water demand in Beibei,Chongqing.The forecasted result is that:water demand of Beibei District is245 millionm3in 2015,and 269 million m3for the year of 2020.
graymodel;secondorder weakening operator;water demand forecast;accuracy
TV213.4
A
1001-5485(2010)07-0012-05
20100128
中央高校基本科研业务费专项资金项目(XDJK2009C066);西南大学光炯基金资助项目(20600901)
杜 涛(1988),男,河北承德人,本科生,主要从事水文与水资源的研究,(电话)13594214550(电子信箱)dtgege@126.com。
叶 琰(1977),男,四川仁寿人,讲师,主要从事流域水资源规划与管理研究和教学工作,(电话)13983380210(电子信箱)yye_china@126.com。
