明渠混合污染物侧向和垂向扩散系数的计算方法及其应用
2010-09-05武周虎胡德俊徐美娥
武周虎,胡德俊,徐美娥
(青岛理工大学环境与市政工程学院,山东青岛 266033)
明渠混合污染物侧向和垂向扩散系数的计算方法及其应用
武周虎,胡德俊,徐美娥
(青岛理工大学环境与市政工程学院,山东青岛 266033)
明渠的侧向和垂向扩散系数是衡量岸边水流对污染物质混合输移能力的重要水质参数之一,其值的准确与否直接关系到明渠水质预测预报成果的可靠性。基于污染混合区的理论计算方法,推导了污染混合区外边界标准曲线和曲面的统一方程,包含最大长度Ls、最大宽度bs和最大深度ds等特征尺度。该曲线形状近似于半椭圆,曲面形状为近似椭球体的一部分,表明污染混合区具有相似性。给出了由岸边污染混合区外边界最大长度、最大宽度或最大深度和平均流速确定侧向或垂向扩散系数的计算公式,提出了采用污染混合区面积或体积进行总体控制的侧向或垂向扩散系数计算方法和采用水面横向积分浓度确定垂向扩散系数的实用方法。通过现场观测结果分析,给出了府河下游河段枯水期的侧向扩散系数0.27 m2/s。
明渠;污染混合区;标准曲线;侧向扩散系数;垂向扩散系数;计算方法
1 概 述
明渠沿岸地区工业或城镇生活污水经处理达到相应的排放标准后,大多数情况是通过管道或明渠实施岸边排放。污水首先在排污口近区稀释混合,其次在水域的长度与宽度、深度方向逐渐移流扩散,在排污口附近水域会形成污染混合区[1]。对于宽阔河流的污染混合区分布多属于二维问题[2,3],而对于宽阔深水水库的污染混合区分布则多属于三维问题[4,5]。另一方面,明渠岸边附近水体常常是人们生产生活用水对水质要求较高的区域,对大江大河来说,“总体水质”不超标,并不意味着“岸边水质”不超标。“岸边水质”对应“岸边环境容量”[6]。
明渠的横向和垂向扩散系数是衡量水流对污染物质混合输移能力的重要水质参数之一,其值的准确与否直接关系到明渠水质预测预报成果的可靠性。目前国内外确定河流横向和垂向扩散系数的主要方法有理论公式、经验公式法和示踪实验法,艾尔德采用对数流速分布函数,在各向同性紊动条件下得出垂向扩散系数为Ez=0.067HU (式中H为断面平均水深,U 为摩阻流速)。由于无量纲横向扩散系数经验公式αy=Ey/HU 一般认为其值为0.3~0.9[7],所以横向扩散系数的计算结果是一个范围值,其准确性难以判定。示踪实验法分为现场实验和室内实验,示踪实验完成后可采用矩法[8-14]、直线图解法[15,16]、线性回归法[17]、曲线拟合法[18]、遗传算法[19]、人工神经网络法[20]等计算横向扩散系数。现场实验法计算结果比较可靠,但河流实验受示踪剂的投放、取样等条件的限制;室内实验多用于水槽中横向扩散系数与粗糙形式、宽度、水深、流速、摩阻流速等水力要素的关系研究。郑旭荣等[21]借助于抛物线型断面形态方程,提出了横向紊动扩散系数的断面分布及其平均值表达式。现行关于横向扩散系数的关系式和数值都是针对河流全断面混合特性的研究成果。实际工程中常见的多为岸边排放,对于宽阔的明渠(如长江、黄河、三峡水库等)水流对污染物质混合输移能力主要取决于岸边混合扩散特性,大江大河岸边污染混合区和岸边环境容量的计算往往只涉及到全断面宽度的数十分之一甚至于数百分之一,选择采用全断面平均水深等水力要素确定的横向扩散系数显然不尽合理,侧向扩散系数比横向扩散系数能更好地反映岸边水流的混合扩散特性。如三峡水库万州段的平均水深为71m,而岸边扩散区的水深比较浅,并且往往处于一个由倾斜岸坡形成的角形变化域。
本文以顺直宽阔的明渠水流对污染物质的混合输移研究为背景,基于武周虎等[2-5]提出的岸边污染混合区理论计算方法,推导污染混合区外边界等浓度标准曲线和曲面的统一方程,提出确定侧向扩散系数和垂向扩散系数的计算公式。采用府河岸边污染混合区的现场观测结果计算其侧向扩散系数,为进一步解决大江大河、水库岸边污染混合区和岸边环境容量的计算问题,提供一定的参考研究。
2 侧向扩散系数计算方法
2.1 河流二维问题

式中:x为自排污口沿河流主流向的纵坐标;y为垂直于x的横向坐标,坐标原点取在岸边排污点;m为单位时间的排污强度;U为岸边水域平均流速;H为平均水深;Ey为岸边排污的横向扩散系数,又称侧向扩散系数①。
由文献[2]给出的岸边污染混合区最大长度Ls、最大宽度bs和相应纵坐标Lc以及面积S的理论计算公式分别为:
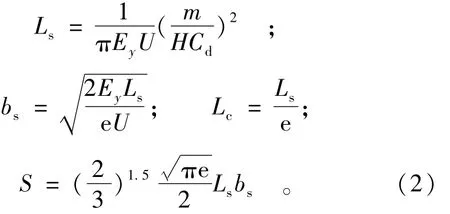
式中Cd为河流排污引起的允许浓度升高值,该值等于水环境功能区所执行的浓度标准值Cs减去背景浓度Cb,即Cd=Cs-Cb,其等浓度线所包围的区域为污染混合区。由式(2)可以得到岸边污染混合区最大长度与最大宽度的比值为

其中Pe=ULs/Ey称为贝克来数,表征物质的纵向移流通量与侧向扩散通量的比值[3]。即岸边污染混合区的长宽比与贝克来数Pe的0.5次方成正比。
将式(2)代入式(1)并令C=Cd,化简整理得到河流岸边污染混合区外边界标准曲线(见图1)方程为
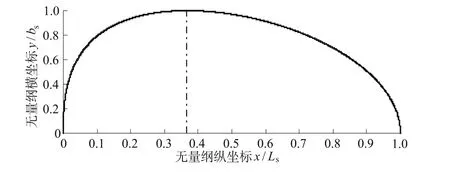
图1 岸边污染混合区外边界标准曲线Fig.1 The standard curve of pollutantm ixing zone’s outer boundary in the bank side
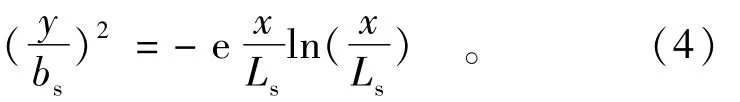
由图1可以看出,河流岸边污染混合区外边界标准曲线形状近似于半椭圆,在靠近排污口一端出现钝头,在污染混合区下游边界出现稍尖形状,污染混合区最大宽度相应的纵坐标为最大长度的1/e≈0.368,说明污染混合区具有相似性。
由式(2)可以得到顺直宽阔河流侧向扩散系数的计算公式为:

式(5)给出了侧向扩散系数的3个计算公式。表明顺直宽阔河流侧向扩散系数与岸边污染混合区最大宽度的2次方成正比,与平均流速的1次方成正比,与最大长度的1次方成反比。说明在平均流速相同的条件下,污染混合区最大长度越大侧向扩散系数越小,最大宽度和面积越大侧向扩散系数越大。在实际应用中,可根据岸边污染混合区的现场观测结果采用式(5)计算侧向扩散系数。
通常,受天然河道地形的影响,污染混合区的形状一般不会像式(4)、图1所示的那么规则,污染混合区最大宽度的测量受多种因素的影响也会存在变数。为了减小污染混合区最大宽度测量不精确给侧向扩散系数计算带来的误差,可以根据现场观测数据绘制污染混合区外边界等浓度曲线,在污染混合区形状大体为上游出现钝头和下游出现稍尖的近似椭圆形情况下,即在最大宽度相应的纵坐标大约为最大长度的1/e时确定其面积(其它形状污染混合区的侧向扩散系数较为复杂,另文研究),然后按照式(5)计算侧向扩散系数,即采用污染混合区面积进行总体控制的侧向扩散系数计算方法,下同。
①Mixing Zone Technical Procedures Manual(DRAFT),Idaho Department of Environmental Quality,USA,2008.8
2.2 倾斜岸水库三维问题

式中:x为沿水库主流向的纵坐标;y,z为垂直于x的横向和垂向坐标,坐标原点取在库岸水面排污点;β为角域映射系数,当岸坡线与水平线之间的夹角为θ时,β=360/θ,其他符号含义同前。
由文献[4]可知,倾斜岸水库岸边污染混合区在z=0水面上最大长度Ls、最大宽度bs、最大深度ds和相应纵坐标Lc以及面积S的理论计算公式依次为:
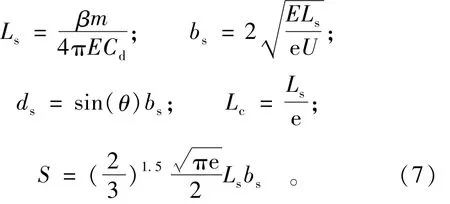
倾斜岸水库岸边污染混合区外边界等浓度标准曲线(宽度)方程与河流二维问题的式(4)、图1相同,污染混合区的空间形状为该等浓度标准曲线在θ角度上的旋转体,是一近似椭球体的扇形截图。
由式(7)可以得到顺直宽阔倾斜岸水库侧向扩散系数的计算公式为

顺直宽阔倾斜岸水库侧向扩散系数与平均流速和水面上污染混合区特征尺度的关系与河流情况相同,只是系数减半。在实际应用中,可根据倾斜岸水库岸边水面上污染混合区的现场观测结果采用式(8)计算侧向扩散系数。
2.3 垂直岸水库三维问题

式中符号含义同前。
由文献[5]可知,垂直岸水库岸边污染混合区在z=0水面上最大长度Ls、最大宽度bs以及面积S和在y=0垂直面上最大深度ds以及相应纵坐标Lc的理论计算公式依次为:
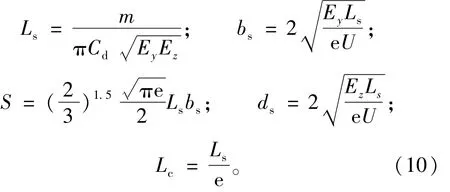
垂直岸水库岸边污染混合区外边界等浓度标准曲线(宽度和深度)方程分别与河流二维问题的式(4)、图1相同,污染混合区的空间形状为1/4近似椭球体的扁蛋形。将式(10)代入式(9)并令C=Cd,化简整理得到该曲面方程为

由式(10)可以得到顺直宽阔水库侧向扩散系数的计算公式为:
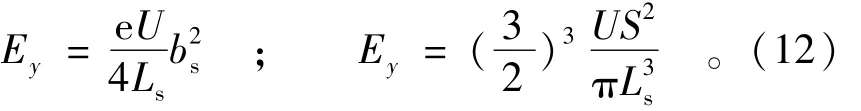
顺直宽阔垂直岸水库侧向扩散系数与平均流速和水面上污染混合区特征尺度的关系与倾斜岸水库情况相同。在实际应用中,可根据垂直岸水库岸边水面上污染混合区的现场观测结果采用式(12)计算侧向扩散系数。
3 垂向扩散系数计算方法
针对垂直岸水库三维问题,在横向和垂向扩散系数不相等的情况下,讨论垂向扩散系数的计算方法。
3.1 垂直面上污染混合区法
根据垂直面上岸边污染混合区外边界标准曲线的特征尺度,按照与侧向扩散系数相同的方法,由式(10)可以得到顺直宽阔水库垂向扩散系数的计算公式为:
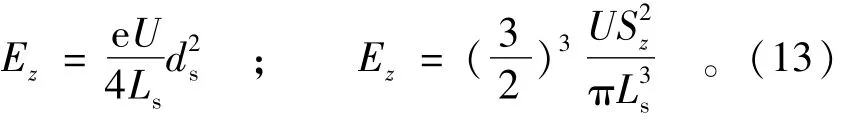
式(13)表明顺直宽阔垂直岸水库垂向扩散系数与垂直面上岸边污染混合区最大深度的2次方成正比,与平均流速的1次方成正比,与最大长度的1次方成反比。说明在平均流速相同的条件下,污染混合区最大长度越大垂向扩散系数越小,最大深度和垂直面积Sz越大垂向扩散系数越大。在实际应用中,根据垂直岸水库岸边垂直面上污染混合区的现场观测结果采用式(13)计算垂向扩散系数。
3.2 岸边污染混合区体积法
根据岸边污染混合区体积计算垂直岸水库的垂向扩散系数是考虑到受天然水库地形的影响,岸边污染混合区的空间形状一般不会像式(11)给出的那么规则,垂直面上岸边污染混合区最大深度和面积的测量受多种因素的影响也会存在变数。为了减小垂直面上岸边污染混合区最大深度和面积测量不精确给垂向扩散系数计算带来的误差,可以根据现场观测数据采用数值积分求和方法计算岸边污染混合区(云团)的体积,然后根据岸边污染混合区体积进行总体控制计算垂向扩散系数。
由文献[5]可知,垂直岸水库三维问题岸边污染混合区体积的理论计算公式为


式(15)表明顺直宽阔垂直岸水库垂向扩散系数与平均流速和岸边污染混合区体积的2次方成正比,与最大长度的4次方成反比,与侧向扩散系数的1次方成反比。说明在平均流速相同的条件下,岸边污染混合区最大长度和侧向扩散系数越大垂向扩散系数越小,污染混合区体积越大垂向扩散系数越大;在侧向扩散系数相同的条件下,平均流速和体积越大垂向扩散系数越大,而岸边污染混合区最大长度越大垂向扩散系数越小。
在实际应用中,根据垂直岸水库岸边污染混合区的现场观测结果采用式(15)计算垂向扩散系数。观测数据包括岸边污染混合区范围内的平均流速、岸边污染混合区的最大长度和体积以及由2.3节中计算方法观测求得的侧向扩散系数。
3.3 水面横向浓度积分法
当z=0时,由式(9)得到垂直岸水库三维问题的岸边水面等强度时间连续点源条件下的水面污染物浓度分布为
由式(10)和式(14)可以得到顺直宽阔水库垂向扩散系数的计算公式为

将式(16)对y积分得到水面横向积分浓度CwI为


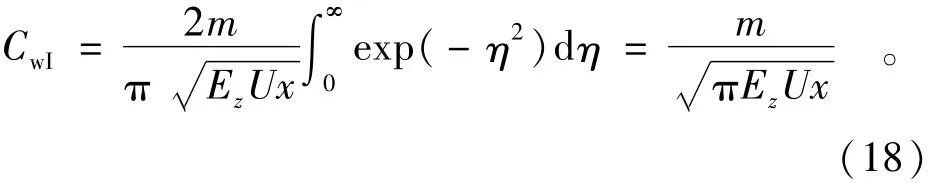
由式(18)可以看出,水面横向积分浓度公式中没有出现侧向扩散系数Ey。这样就可以根据垂直岸水库岸边排污口下游距离x0处水面横向浓度分布的观测资料求得水面横向积分浓度CwI,然后利用下式计算垂向扩散系数

式(19)表明顺直宽阔垂直岸水库垂向扩散系数与平均流速和排污口下游距离的1次方成反比,与水面横向积分浓度的2次方成反比,与排污强度的2次方成正比。说明在排污强度相同的条件下,水面横向积分浓度越大垂向扩散系数越小。即垂向扩散系数越小,向深水区扩散的污染物就会越少,大量污染物就会聚集在水面附近的浅层水体。对水库水面中心排放条件式(19)同样适用,此时水面横向积分浓度CwI的积分区间是断面全宽度。
根据水面横向浓度积分法计算垂向扩散系数,使现场观测工作得到了大大地简化,无需在深水区大量采样观测其空间浓度分布。观测水面横向浓度分布既省时省力,又容易保证观测精度。建议水面横向浓度分布的观测选在污染混合区最大宽度出现的断面附近,该断面污染物浓度相对较高,污染物浓度分布较宽,有利于保证精度。
4 现场观测结果分析
氵光府河发源于泰山山脉,流经泰安、济宁两地市入南四湖的南阳湖北端,流域面积1 331 km2。作者于2005年3月枯水期调研时,在济宁市河路大桥附近右岸发现某淀粉厂向府河大量排放超标淀粉废水,在排污口附近下游形成清晰可辨的白色污染混合区,当即进行了现场拍照和测量,图2给出了该淀粉厂岸边排污口污染混合区现场观测示意图。经现场测量该淀粉厂岸边高浓度白色污染混合区外边界最大长度Ls和最大宽度bs分别为32 m和5 m,最大宽度相应的纵坐标Lc为12 m,污染混合区范围内的平均流速U为0.25 m/s,该河段水面宽度B为72 m。
氵光府河顺直宽阔,而且纵向移流作用较强,排放岸边高浓度白色污染混合区的色度基本不受对岸边界反射的影响。将现场观测的最大长度和最大宽度代入式(4)得到该淀粉厂岸边高浓度白色污染混合区外边界(等色度)曲线方程为
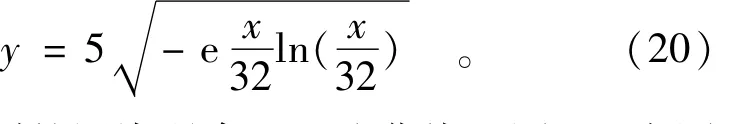
由式(20)绘制的污染混合区理论曲线见图2。由图2可以看出,由现场观测的最大长度和最大宽度确定的污染混合区理论曲线与拍照的该淀粉厂岸边高浓度白色污染混合区外边界吻合良好,最大宽度相应的纵坐标理论值Lc=Ls/e=11.8 m与现场观测值12 m非常接近,说明河流保守物质平面二维移流扩散简化方程以及由此得到的理论公式适用于府河污染混合区的计算。因此,可采用式(5)计算府河侧向扩散系数为


图2 氵光府河某淀粉厂岸边排污口污染混合区现场观测示意图Fig.2 The observation of pollutantm ixing zone at some starchy factory’s outfall near Guangfu River bank
顺直宽明渠混合污染物侧向扩散系数计算方法涉及的现场观测数据主要是岸边污染混合区外边界最大长度、最大宽度和污染混合区范围内的平均流速共3个要素,对已有排污口的现场观测在岸边污染混合区外边界线清晰可辨时更为简单方便,快捷灵活,利于掌握。一般情况下,需进行现场水流水质同步监测,即在已有排污口邻近上游和下游污染影响区布设若干个断面和垂线,监测流速和水质指标,同时测定排污强度以及河流水文水力要素。然后,根据水质监测结果绘制一系列等浓度线并计算相应的平均流速,在等浓度线与式(4)表示的标准曲线吻合较好时,采用式(5)计算侧向扩散系数,分析侧向扩散系数与河流水文水力要素和污染混合区尺度的关系。
5 结 论
(1)推导了顺直宽阔明渠岸边污染混合区外边界标准曲线和曲面的统一方程,包含最大长度Ls、最大宽度bs和最大深度ds等参数,曲线形状近似于半椭圆,空间形状为近似椭球体的一部分,表明污染混合区具有相似性。
(2)给出了顺直宽阔明渠混合污染物侧向和垂向扩散系数的理论计算公式,表明侧向和垂向扩散系数可以根据污染混合区特征尺度和平均流速来计算,还提出了采用水面横向积分浓度确定垂向扩散系数的实用方法。
(3)通过现场观测结果分析,给出了氵光府河下游河段枯水期的侧向扩散系数Ey=0.27 m2/s。
[1] 张永良,李玉梁.排污混合区分析计算指南[M].北京:海洋出版社,1993:3-9.(ZHANG Yong-liang,LI Yu-liang.Companion of Analytical Calculation to the Pol-lutant Mixing Zone in the Outfall’s[M].Beijing:Ocean Press,1993:3-9.(in Chinese))
[2] 武周虎,贾洪玉.河流污染混合区的解析计算方法[J].水科学进展,2009,20(4):544-548.(WU Zhou-hu,JIA Hong-yu.Analytic method for pollutant mixing zone in river[J].Advances in Water Science,2009,20(4):544-548.(in Chinese))
[3] 武周虎.明渠移流扩散中无量纲数与相似准则及其应用[J].青岛理工大学学报,2008,29(5):17-22.(WU Zhou-hu.The concept and its application of the dimen-sionless numbers&conform rules by advection-diffusion in the open channel flow[J].Journal of Qingdao Tech-nological University,2008,29(5):17-22.(in Chi-nese))
[4] 武周虎.倾斜岸水库坡地形污染混合区的三维解析计算方法[J].科技导报,2008,26(18):30-34.(WU Zhou-hu.3-D Analytic computationalmethod of pollutant mixing zone for reservoir with incline bank[J].Science&Technology Review,2008,26(18):30-34.(in Chi-nese))
[5] 武周虎.水库铅垂岸地形污染混合区的三维解析计算方法[J].西安理工大学学报,2009,25(4):436-440.(WU Zhou-hu.3-D analytic computationalmethod of pol-lutantmixing zone for reservoir with vertical bank[J].Journal of Xi’an University of Technology,2009,25(4):436-440.(in Chinese))
[6] 黄真理,李玉粱,李锦秀,等.三峡水库水环境容量计算[J].水利学报,2004,35(3):7-16.(HUANG Zhen-li,LIYu-liang,LI Jin-xiu,et al.Water environ-mental capacity for the reservoir of Three Gorges Project[J].Journal of Hydraulic Engineering,2004,35(3):7-16.(in Chinese))
[7] FISCHER H B,IMBERGER J,LIST E J,et al.Mixingin Inland and CoastalWaters[M].New York:Academic Press,1979,107-112.
[8] ELDER JW.The diffusion ofmarked fluid in turbulent shear flow[J].Fluid Mechanics,1959,5(4):544-560.
[9] LAU Y L,KRISHNAPPAN B G.Transverse dispersion in rectangular channels[J].Journal of Hydraulics Divi-sion,ASCE,1977,103(10):1173-1189.
[10]HOLLEY E R,SIEMOUS J,ABRAHAM G.Some as-pects of analyzing transverse diffusion in rivers[J].Jour-nal of Hydraulic Research,1972,10(1):27-57.
[11]DEMETRACOPOULOS A C,STEFAN H G.Transverse mixing in wide and shallow river:case study[J].Journal of Environmental Engineering,ASCE,1983,109(3):685-697.
[12]周 云.天然河流横向混合系数的研究[J].水利学报,1988,19(6):54-60.(ZHOU Yun.Study on trans-verse diffusion coefficient in natural river[J].Journal of Hydraulic Engineering,1988,19(6):54-60.(in Chi-nese))
[13]李 玲,李玉梁,陈嘉范.梯形断面水槽中横向扩散系数的实验[J].清华大学学报(自然科学版),2003,43(8):1124-1126,1152.(LI Ling,LI Yu-liang,CHEN Jia-fan.Experimental study on transverse diffusion coefficients in an open trapezoidal channel[J].Journal of Tsinghua University(Science and Technology),2003,43(8):1124-1126,1152.(in Chinese))
[14]郭建青,郑鹏海.确定河流横向扩散系数的改进矩法[J].水电能源科学,1998,16(4):32-35.(GUO Jian-qing,ZHENG Peng-hai.The improved moment method for determining the transverse diffusion coefficient of river stream[J].International Journal Hydroelectric Energy,1998,16(4):32-35.(in Chinese))
[15]梁秀娟,刘耀莹,张文静,等.室内模拟试验确定横向扩散系数的研究[J].吉林大学学报(地球科学版),
2004,34(4):560-565.(LIANG Xiu-juan,LIU Yao-ying,ZHANGWen-jing,et al.The study of determining the transverse diffusion coefficient of river through the in-door simulation experiments[J].Journal of Jilin Univer-sity(Earth Seience Edition),2004,34(4):560-565.(in Chinese))
[16]郭建青,张 勇.确定河流横向扩散系数的直线图解法[J].水利学报,1997,28(1):62-67.(GUO Jian-qing,ZHANG Yong.Linear graphicsmethod for determi-ning the transverse diffusion coefficient of river[J].Jour-nal of Hydraulic Engineering,1997,28(1):62-67.(in Chinese))
[17]郑鹏海,郭建青.确定河流横向扩散系数的线性回归法[J].水电能源科学,1999,17(3):17-19.(ZHENG Peng-hai,GUO Jian-qing.The linear regression method for determining the transverse diffusion coefficientof river stream[J].International Journal Hydroelectric Energy,1999,17(3):17-19.(in Chinese))
[18]龙炳清,赵仕林,周后珍,等.岷江蕨溪段环境水力学研究——横向扩散[J].四川师范大学学报(自然科学版),2001,24(4):372-374.(LONG Bing-qing,ZHAO Shi-lin,ZHOU Hou-zhen,et al.The study of en-vironmental hydraulics for Juexi section in min river——transverse diffusion[J].Journal of Sichuan Normal Uni-versity(Natural science),2001,24(4):372-374.(in Chinese))
[19]金保明,杨晓华,金菊良,等.确定河流横向扩散系数的实码遗传算法[J].水电能源科学,2000,18(1):9-12.(JIN Bao-ming,YANG Xiao-hua,JIN Ju-liang,et al.Real coding genetic algorithm for determining the transverse diffusion coefficient of river[J].International Journal Hydroelectric Energy,2000,18(1):9-12.(in Chinese))
[20]龙腾锐,郭劲松,冯裕钊,等.二维水质模型横向扩散系数的人工神经网络模拟[J].重庆环境科学,2002,24(2):25-28.(LONG Teng-rui,GUO Jing-song,FENG Yu-zhao,et al.Modulus of transverse diffuse sim-ulation based on artificial neural network[J].Environ-mental Science of Chongqing,2002,24(2):25-28.(in Chinese))
[21]郑旭荣,邓志强,申继红.顺直河流横向紊动扩散系数[J].水科学进展,2002,13(6):670-674.(ZHENG Xu-rong,DENG Zhi-qiang,SHEN Ji-hong.Transverse turbulent dispersion coefficient in straight channel[J].Advances in Water Science,2002,13(6):670-674.(in Chinese))
(编辑:周晓雁)
Calculation M ethod of Lateral and Vertical Diffusion Coefficients for M ixed Pollutant in Open Channel Flow and Its App lication
WU Zhou-hu,HU De-jun,XU Mei-e
(Institute of Environmental Engineering,Qingdao Technological University,Qingdao 266033,Shandong)
Lateral and vertical diffusion coefficients of open channel is one of importantwater quality parameters to measure themixedly transporting capacity of pollutants near the bank flow.Whether the value is accurate or not is directly related to the reliability of thewater quality forecast in open channel flow.Based on the theoretical calcula-tionmethod of pollutantmixing zone,the unified equation of the standard curve and curved surface outside the bor-ders of pollution mixing zone is deduced,including the characteristic parameters of themaximum length Ls,maxi-mum width bsandmaximum depth dsetal.The shape of the curve approximates to a semi-ellipse,and the shape ofcurved surface is akin to a partof ellipsoid,which shows the pollution of themixing zone has similarity.The calcu-lation equation for determining the lateral or vertical diffusion coefficient by themaximum length,maximum width ormaximum depth of the outer boundary of pollutantmixing zone and themean velocity is given.The calculation method of the lateral or vertical diffusion coefficient which is overall controlled by the area or volume of pollutant mixing zone,and the practicalmethod of vertical diffusion coefficient which is determined by the concentration of surface transverse integration,are proposed.By analyzing the data of field observation,the lateral diffusion coeffi-cient of the downstream of Guangfu River in low water season is 0.27 m2/s.
open channel;pollutantmixing zone;standard curve;lateral diffusion coefficient;vertical diffusion coefficient; calculation methods
X522,X524
A
1001-5485(2010)010-0023-07
2010-08-23
国家自然科学基金项目(50979036),国家水体污染控制与治理科技重大专项(2009ZX07210-007-01)
武周虎(1959-),男,陕西岐山人,教授,主要从事环境水力学与水污染防治研究,(电话)13061205508(电子信箱)wu_zh2008@yahoo.com.cn。
