基于GPS的电力系统高精度同步时钟

杨其岚,万 全

(1.五凌电力有限公司,湖南长沙 410004;2.湖南省电力公司试验研究院,湖南长沙 410007)

当前电力系统广域保护、安全稳定监测、控制、同步通讯和远动等领域已提出了不少基于高精度时钟的测量、监测与控制技术。现有的同步时钟技术绝大部分采用美国的 GPS时钟或俄罗斯的GLONASS时钟为基准,但并不保证时钟的可靠性,也不对民用用户承担责任。同时 GPS及 GLONASS接收器接受到的时钟也经常因星历误差、卫星钟差、电离层误差、对流层误差、多径误差、跟踪卫星过少误差和接收器本身误差等产生一些误差。目前国内外研制了一些 GPS同步时钟产品,但采用铯钟或铷钟对 GPS时钟修正产生的高精度同步时钟价格很高,运行环境要求苛刻,难以推广;而一般电力系统运行的时钟却不能保证输出时钟的稳定性,很难在一些对时钟精度和稳定性要求高的关系电力系统经济与稳定运行的重要领域 (如电力系统继电保护、在线监控等领域)中得到实际应用。本项目提出采用晶振信号同步 GPS信号产生高精度时钟的一元二次回归数学模型,研制时钟发生装置。该方法既消减了 GPS时钟信号的随机误差,又消除了晶振时钟信号的累计误差,且易于实现,有望成功应用于电力系统继电保护与控制。

1 晶振信号同步 GPS信号的方法

为产生高精度时钟信号,采用计数器和比较器对高精度晶振进行分频,产生晶振秒时钟信号;晶振秒时钟与 GPS秒时钟进行相位比较,产生偏差序列,偏差包括 GPS时钟的随机漂移误差和晶振的累计误差;采用一元二次回归分析模型对 2种误差进行估计,分离出各自误差;并对晶振累计误差进行修正,可以构造出一种简便的高精度时钟发生装置。实现方案如图 1所示,高精度时钟 (修正后的秒时钟)由计数器与比较器构成的分频电路产生,晶振秒时钟的累计误差由 CPU设置比较值进行修正,GPS秒时钟误差由锁存器测量。比较值每秒设置 1次,本次将要设置的比较值由前 n次测量的 GPS秒时钟误差和前 n次设置的比较值历史数据进行计算。

图 1 高精度时钟产生的原理图

1.1 晶振信号同步 GPS信号的一元二次回归模型

在目前的 GPS接收器中,GPS输出秒时钟与国际标准时间 (UCT)存在一定的随机误差 ε。考察某一秒时间序列,第 x个秒时钟的时间误差 εx服从正态分布

不同质量的 GPS接收器,σ数值大小不同,如 GARMIN GPS25/20为 1μS,而 MOTOROLA VP ONCORE则为 50nS。

由于高精度晶振的随机误差远小于 GPS秒时钟的随机误差 (如稳定度为 10-9的晶振分频产生的秒时钟随机误差小于 1 nS),因此不考虑晶振秒时钟的随机误差。根据文献 〔2〕介绍,仅考虑晶振的频率偏差及频率的线性漂移,由晶振分频产生秒时间序列的第 x个秒时钟的时间误差 μ(x)可表示为

式中 a为秒时间序列的初始误差;b为考虑频率偏差的误差系数;c为考虑频率线性漂移的误差系数。

由式 (1)和 (2)得晶振分频秒时钟 (简称晶振秒时钟)与 GPS秒时钟之间的偏差为

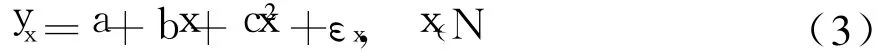
1.2 高精度时钟的产生

(1)GPS接收器工作状态的评估

GPS接收器的不正常工作状态分为 2种,一种是由于跟踪卫星过少,导致随机误差增大;另一种是由于干扰,GPS故障产生的跳跃性误差。

对于第一种误差采用 GPS时钟方差的估计值σ^2进行评价,建立评价不等式

式中 σs为 GPS接收器说明书中对应 1σ的标称误差;k1为可靠系数,通常取 1.5～5。当上式成立时,认为 GPS接收器工作不正常。

对于第二种误差采用 GPS秒时钟与修正后的秒时钟的误差序列 Φ进行评价。按正态分布分析理论,GPS接收器正常工作时落于 3σ^范围外的概率仅约为 0.002 6。在样本误差序列 Φ中对大于3σs的数据个数 Nb进行统计,建立评价不等式

式中 k2为可靠系数,通常取 2～10。当上式成立时,同样认为 GPS接收器工作不正常。

(2)GPS接收器正常运行条件下高精度时钟的产生

根据晶振秒时钟误差参数的估计值 a^,b^,^c,计算 (n+1)次晶振秒时钟的累计误差估计值

从而 (n+1)次晶振误差的补偿值为

对 μ^(n+1)四舍五入取整,记为:R〔μ^(n+1)〕,则有

从而由 CPU实时设置补偿值来控制 CPLD产生修正后的高精度秒时钟。

(3)GPS接收器不正常运行条件下高精度时钟的产生

由于高精度恒温晶振时钟的稳定度较高、误差漂移小,在 GPS接收器不正常运行条件下,b^,^c恒定取 GPS接收器不正常运行以前的值,秒时间序列的初始误差估计值 a^恒定取零,同样按式(6)和 (8)计算产生修正晶振秒时钟的比较值。

假设晶振的精度为 1 nS,晶振秒时钟二阶以上的误差漂移小于 0.05nS,则在 GPS接收器中断运行1h后,输出的修正后的秒时钟误差小于180nS;考虑极端情况,在 GPS接收器中断运行1 d后,输出的修正后秒时钟误差小于 4 320 nS。通常 GPS接收器中断运行 1 h,补偿后输出的时钟能够满足一般控制领域的要求。

2 高精度同步时钟的具体实现

根据上述原理,文中设计出了一种 GPS同步高精度时钟,其原理如图 2所示。GPS同步的高精度时钟主要由 GPS接收器、CPLD,CPU,50MHz恒温高精度晶振和串行接口等组成。

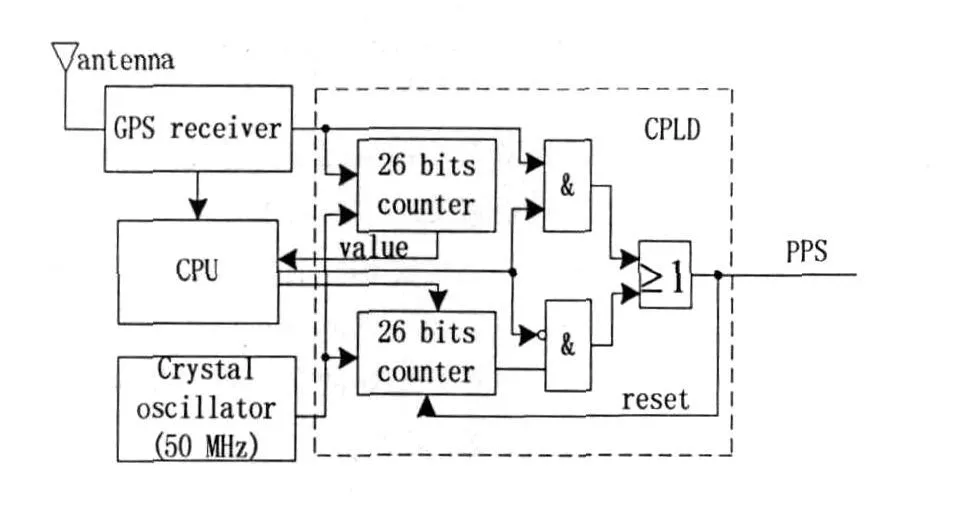
图 2 高精度时钟的硬件框图

GPS接收器产生的 GPS秒脉冲信号锁存计数结果,由 CPU记录 GPS时钟的随机误差。CPU根据 GPS随机误差序列和整定值序列,计算 GPS秒时钟与晶振秒时钟的偏差序列,并对 GPS秒时钟的方差 σ2、晶振秒时钟序列与国际标准时间的初始误差 a、反映晶振秒时钟周期误差的参数 b及反映晶振秒时钟周期误差漂移的参数 c进行最小二乘估计。由 GPS秒时钟方差的估计值判断 GPS接收器的工作状况。然后,生成对晶振秒时钟修正的比较值,通过调整比较值来消除晶振秒脉冲的累计偏差,使修正后的秒脉冲偏差小于 0.1μS。其具体工作过程如下:

(1)GPS接收器状态的判断

GPS接收器的状态分为正常状态和不正常状态2种。在具体工作中由 CPU根据评价不等式 (4),(5)进行判断:当上述评价不等式中有 1个成立时,认为 GPS接收器工作不正常;否则,当 2个评价不等式都不成立时,认为 GPS接收器工作正常。

(2)精确秒时钟的产生

50 MHz恒温高精度晶振产生 50 MHz时钟信号,由 CPLD中的 26位计数器对秒时钟计数,并将计数结果发送给 CPU。当 CPU判断出 GPS接收器的工作状态后,如果接收器工作正常,由当前估计的参数根据式 (8)计算晶振秒脉冲的补偿值;如果接收器工作不正常,则由不正常工作以前估计的参数计算补偿值。然后将补偿值与秒时钟计数值相结合产生修正值。最后由 CPLD根据修正值产生修正后的高精度秒时钟。

3 MAX PLUSⅡ仿真及分析

CPLD采用 Altera公司的 EPM7128,仿真软件为 MAX PLUSⅡ。在做仿真实验时,由于计算机资源不足,无法进行秒级的仿真实验,文中用频率为 100 Hz的信号代替秒脉冲,其它信号仍按实际情况处理,仿真 50ms的时间。图 3～6反映的是同一次仿真的 4个不同片断。

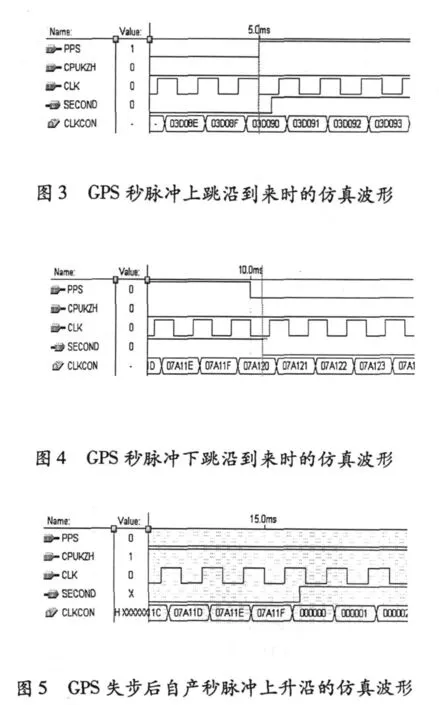
图 6 GPS失步后自产秒脉冲下降沿的仿真波形

从图 3,4可以看出:GPS接收器工作正常时(CPUKZH端置 “0”),输出端 (SECOND端)的波形滞后于输入端 (PPS端)的波形,门时延为6.5ns。从图 5和图 6可以看出:GPS接收器工作不正常时 (CPUKZH端置 “1”),输出端(SECOND端)的自产秒脉冲 (由晶振计数产生)在计数器计满 07A120H(仿真时由固定值替代CPU发送的修正值)个数时置 “1”,在计数器计到 03D090H个数时置 “0”,门时延为 7.4ns。

上述仿真结果是在理想状态下产生的,没有考虑实际情况,装置在实际工作中的误差要比仿真值大许多。其误差来源除去可由软件校正的误差外,还有 2个方面:a.晶振时钟的上跳沿要滞后于秒时钟的上跳沿 (不同步),其误差最大可达 20ns;b.CPLD中的门延时及计数器清零、计数所需的延时,由仿真结果可以看出这 2项误差之和不会超过1个计数周期,即 20 ns。

4 结束语

文中提出采用晶振信号同步 GPS信号产生高精度时钟的一元二次回归数学模型,对 GPS时钟进行在线监测和校正,减少 GPS时钟随机误差和因卫星失锁等原因产生误差的影响,通过对晶振时钟计数比较值的在线调整,产生高精度时钟。该方法既消减了 GPS时钟信号的随机误差,又消除了晶振时钟信号的累计误差,且易于实现,有望成功应用于电力系统继电保护与控制、故障测距、稳定判断与控制等领域。

〔1〕 Lewandowski W.,Petit G.,Thomas C.Precision and accuracy of GPS time transfer〔J〕.IEEE Transactions on Instrumentation and Measurement,1993,42(2).

〔2〕曾祥君,尹项根,K.K.Li,W.L.Chan.GPS时钟在线监测与修正方法〔J〕.中国电机工程学报,2002,22(12).

〔3〕徐炳垠,李桂义,李京,等.接收 GPS卫星信号的电力系统同步时钟 〔J〕.电力系统自动化,1995,19(3).

〔4〕高厚磊,贺家李,江世芳.基于 GPS的同步采样及在保护与控制中的应用 〔J〕.电网技术,1995,19(7).

〔5〕 Conley R.,Lavrakas J.W.Global implications on the removal of selective availability〔J〕.Proceedings of the 2000 IEEE Position Location and Navigation Symposium.2000,506-513.

〔6〕 Crossley,P.Future of the Global Positioning System in power systems〔J〕.IEE colloquium on developmentsin the Use of Global Positioning Systems,Feb.8,1994.7/1-7/5.