机械可靠性优化设计的应用

陈 静郝少祥邵凤翔

(1.中国矿业大学(北京)机电与信息工程学院,北京市海淀区,100083; 2.河南工程学院机械工程系,河南省郑州市,451191)

★煤炭科技·机电与信息化★

机械可靠性优化设计的应用

陈 静1,2郝少祥2邵凤翔2

(1.中国矿业大学(北京)机电与信息工程学院,北京市海淀区,100083; 2.河南工程学院机械工程系,河南省郑州市,451191)

根据机械设计的具体情况,阐述了机械产品优化设计理论及可靠性理论的相关特点,介绍了可靠性优化设计的应用及发展现状,并介绍了机械行业相关的软件应用情况。

机械可靠性 优化设计 软件

1 可靠性设计

机械可靠性设计和优化设计一样,都是20世纪60年代在传统的机械设计基础上发展起来的现代设计方法。传统的机械设计方法又称安全系数法,在设计机械零件时,通常认为零件的强度和应力都是单值,只要计算出的安全系数大于规定的数值,就认为零件是安全的,在设计过程中忽略了各设计参数的随机性。而可靠性设计方法中,将应力作为随机变量,认为应力受到各种环境因素(温度、腐蚀、粒子辐射等)的影响,是一个随机变量,具有一定的分布规律;同样的,强度受材料的性能、工艺环节的波动和加工精度等的影响,也是具有一定分布规律的随机变量。设计时根据不同的设计要求,选取不同的特征函数来描述,既考虑均值,又考虑其离散性,用概率统计的方法求解。可靠性设计认为所设计的任一机械存在着一定的失效可能性,设计时可根据需要预先控制其失效概率或可靠度,考虑各参数的随机性及分布规律,以反映出零部件的实际工作状况。

产品的可靠性表示产品在规定使用条件下和使用期限内,保持其正常技术性能完成规定功能的能力。可靠性设计的一个目标是计算可靠度,可靠度是指产品在规定的条件下和规定的时间内,完成规定功能的概率。表示为:

式中:fX(X)——基本随机参数向量X=(X1, X2,…,Xn)T的联合概率密度;

g(X)——状态函数。

fX(X)的随机参数代表载荷、零部件的特性等随机量。g(X)可表示零部件的两种状态:g (X)小于等于0,为失效状态;g(X)大于0,为安全状态;g(X)=0为极限状态方程,是一个n维曲面,称为极限状态面或失效临界面。

由于在工程实际中,很难有足够的资料来确定计算可靠度所需要的基本随机变量向量X的概率密度函数或联合概率密度函数。即使能够近似地指定其概率分布,而在大多数情况下也很难进行积分计算而获得可靠度,因此一般采用其他的近似方法。至今已出现的计算可靠度的方法主要有:一次二阶矩法、高次高阶矩法、图解渐进法、蒙特卡罗模拟法、响应面法以及随机有限元法等等。

2 机械优化设计

机械优化设计是随着电子计算机的广泛使用而迅速发展起来的一门学科,在现代机械设计中占有重要的地位。优化的目的是以最少的材料,最低的造价,最简单的工艺,实现机械结构的最优性能,包括强度、刚度、稳定性等目标。机械优化设计追求最合理的利用材料的性能,使各个部件或零件的几何参数得到最好的协调,使设计者从众多的设计方案中获得较为完善的或最为合适的最优设计方案。

3 可靠性优化设计

可靠性优化设计方法是在常规优化设计方法的基础上,结合可靠性设计理论发展起来的一种有效的优化设计方法。它将可靠性分析理论与数学规划方法有机地结合在一起,也就是在优化设计中将设计参数作为随机变量,以产品的可靠度作为目标函数或约束条件,运用最优化方法得到在概率意义下的最佳设计的一种数值计算方法。由于它弥补了单一可靠性设计或优化设计的不足,使设计不仅符合工况运行要求,而且得出最优的设计参数,因而更具有工程实用价值,对它的研究已成为目前国内外学者积极探索和研究的重要领域之一。

优化设计数学模型的3个要素是目标函数、约束条件和设计变量。相对于常规的优化设计,可靠性优化设计的特点在于将可靠性设计引入优化设计当中。将可靠性设计理论与优化技术结合起来通常有下面两种方法:

(1)要求结构或零部件在满足一定性能的条件下,使其可靠度达到最大。可按可靠性指标建立一个目标函数,而按设计其他要求建立另一个或多个目标函数,然后进行多目标函数优化设计。其数学模型如下:

式中:R(X)——可靠性函数;

Fi(X)——某一目标函数;

Gj(X)——约束条件。

(2)在结构或零部件达到最佳性能指标时,要求它的工作可靠度不低于某一规定水平。可将可靠性指标作为约束条件,建立数学模型,进行优化设计。一般说来,这种方法更为实用。其数学模型如下:

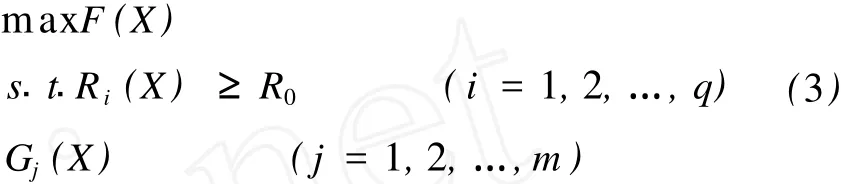
式中:F(X)——目标函数;

Ri(X)——机械产品的可靠性函数;

R0——给定的可靠度;

Gj(X)——约束条件。

在进行结构可靠性优化时,除了建立适当的优化模型外,还需要选择收敛速度快且计算不是很复杂的优化算法。由于工程实践中的可靠性优化设计面临着随机不确定性和模糊不确定。随机不确定性反映了对未来结果的不可预测性,用随机概率度量;模糊不确定性反映了对已有现象结果的未确知性,用模糊隶属度度量。对这种模糊性,仅用概率统计的方法来描述显然是不完善的,因此基于模糊数学的模糊可靠性优化设计方法在机械结构设计中得到了一定的应用。近年来,国内外学者还将计算智能技术(CIT)中的神经网络(ANN)、遗传算法(EA)、模拟退火算法(SA)和蚁群算法等应用到结构可靠性优化设计领域中,并取得了良好的效果。

由于可靠性优化设计在科学实验、生产实践上有着广泛的应用前景,其重要意义不言而喻。随着优化设计技术、有限元技术和计算机技术的发展,如何应用软件技术进行可靠性优化设计也引起了各国学者极大的兴趣。比如我国吉林大学的袁涛等人利用Ansys的参数化设计语言APDL实现摄动法的可靠性分析,并结合设计优化模块实现可靠性优化设计,并证明这一方法是可行有效的,开辟了一个利用Ansys进行可靠性优化设计的途径,扩展了Ansys的分析范围。

随着优化设计技术、有限元技术和计算机技术的发展,结构可靠性优化设计已呈现加速发展的态势,必将为机械产品的合理设计与开发起到非常重要的作用。

[1]王启.常用机械零部件可靠性设计[M].北京:机械工业出版社,1996

[2]李晶,鹿晓阳,陈世英.结构优化设计理论与方法研究进展[J].工程建设,2007(12)

[3]黄洪钟.基于模糊失效准则的机械结构广义静强度的模糊可靠性计算理论[J].机械强度,2000(1)

[4]董桂西,王藏柱.结构优化设计的现状及展望[J].电力情报,2000(1)

[5]董玉革,朱文予,陈心昭.机械模糊可靠性计算方法的研究[J].系统工程学报,2000(1)

[6]郑光泽.机械零件的模糊可靠性设计分析[J].重庆工学院学报,2004(4)

[7]袁涛,张义民,薛玉春,贺向东.利用ANSYS实现零件的可靠性优化设计[J].机械设计与制造,2007 (5)

(责任编辑 张艳华)

Opt imal design of mechan ical reliability and software application

Chen Jing1,2,Hao Shaoxiang2,Shao Fengxiang2
(1.School of Electromechanical and Information Engineering,China University ofMining and Technology, Haidian District,Beijing 100083,China; 2.Department ofMechanical Engineering,Henan Institute of Engineering,Zhengzhou,Henan province 451191,China)

Based on practical conditions ofmechanical design,the paper expounds the characteristics pertaining to theory ofoptimal design ofmechanicalproducts andmechanical reliability,with description of the application and developmentofoptimal reliability design and relevant software used in mechanical industry.

mechanical reliability,optimal design,software

TH122

B

陈静(1964-),女,中国矿业大学(北京)在读博士。现任河南工程学院教师,副教授。