基于灰色系统理论的钼粉锥形件压扭成形优化

章 凯, 聂爱琴, 李 萍, 王 成

(合肥工业大学材料科学与工程学院,安徽合肥 230009)

钼和钼合金由于高密度、高熔点、大的高温强度和高温硬度等优点,在航空航天、核工业及军工业中得到了广泛的应用[1,2]。压制成形是目前粉末锥形件制造的常用方法,其制造的锥形件致密度很难达到一些特殊零件(如破甲弹中的关键部件药型罩)的要求[3]。高压扭转成形是在变形体高度方向施加压力的同时,通过主动摩擦作用在其横截面上施加扭矩,促使变形体同时产生轴向压缩和切向剪切变形的特殊塑性成形工艺[4,5]。该工艺一方面保证了法向应力的降低,提高非密实件的可焊性能;另一方面可以使粉末颗粒产生较大的塑性变形,促进颗粒破碎以及孔隙闭合,并能显著改善密度分布[6,7]。粉末锥形件的质量要求满足多个指标,如致密度和密度分布均匀性等。灰色系统理论具有建模和预测的作用,能研究影响因素与目标结果的关联度大小,在多目标优化设计中得到应用。

本研究在试验设计和数值模拟的基础上,利用灰色系统理论的关联度计算,对钼粉锥形件高压扭转成形工艺参数进行优化,以提高平均相对密度,并改善密度分布的均匀性。

1 基于灰色系统理论的优化策略

在灰色系统中,关联度用来描述事件之间、因素之间动态发展态势的相似程度。关联度越大,事件之间的相似程度就越大。根据灰色系统理论,对于多影响因素的设计,不同的设计条件具有不同的量纲、数量级,所以必须进行数据处理。设经过数据变换的基准矢量序列为X0={x0(k),k=1,2,…,n},目标矢量序列为Xi={xi(k),k=1,2,…,n},i=1,2,…,m;m为目标矢量个数。则Xi对于X0在第k点的灰色关联系数为：

其中,ρ为分辨系数,一般取 0.5。

Xi对于X0的关联度为：

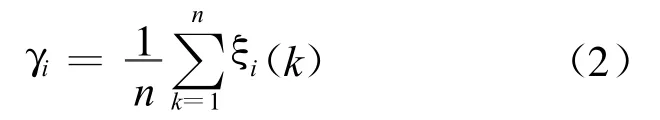
关联度γi越大,目标矢量序列Xi与基准序列X0越相似,由此可判断事物之间的相似性。基于灰色关联度的多目标优化设计步骤为：①对成形工艺参数的序列进行数据规范化;②求出每个单目标与试验工艺参数之间的关联系数;③通过关联度的公式,求出目标函数的关联度,分析灰色关联度序列相对大小,以灰色关联度最大值对应工艺参数值为最优值[8]。

2 有限元模型的建立

2.1 几何及材料建模

模拟采用的锥形件坯料几何参数为：锥角为58°、高度为26.5 mm、壁厚为2.7 mm。

材料参数为：弹性模量E是相对密度ρ的函数,E=E0ρ3.2,初始弹性模量 E0=35000 MPa;泊松比 μ随相对密度 ρ的变化规律为 μ=e-12.5(1-ρ)2/2;屈服应力与相对密度的关系如图1所示,初始相对密度为0.7。

温度参数为：热膨胀系数为4.9×10-6/℃,热导率为35 W/(m◦K),比热为62 J/(kg◦℃)。

材料模型采用Shima模型[9],即

其中,σy为单轴屈服应力;σij′为应力偏张量;P为静水压力;γ、β为材料参数,且均为相对密度的函数。

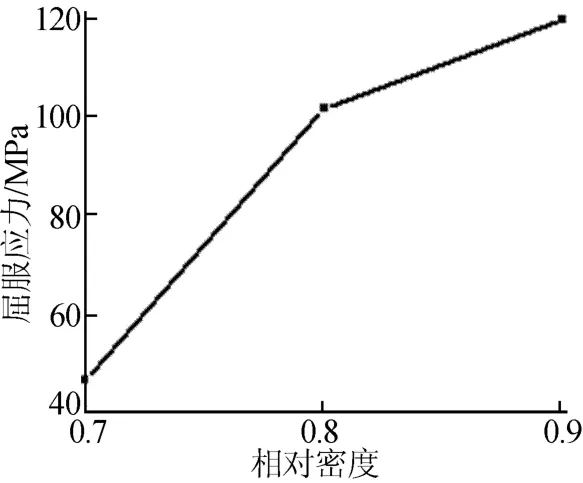
图1 屈服应力随相对密度变化曲线

2.2 网格划分及边界条件确定

有限元分析采用134号四节点四面体实体单元,整个模型划分为26160个单元、5704个节点。考虑了温度的影响,在模拟中采用基于更新的拉格朗日方法的热-机耦合分析方法,即采用与温度场耦合的大变形热弹塑性增量有限元方法。

由于高压扭转成形是依靠摩擦来传递扭转,故选用剪切摩擦模型来定义变形过程中的摩擦行为较为准确。本研究参照国内首台压扭设备,对于有限元分析中上模轴向运动,采用载荷控制方法;下模旋转运动,则采用速度控制方法。整个模拟过程为15 s,划分成150增量步进行分析,有限元模型如图2所示。

图2 锥形件压扭有限元模型

3 试验设计及模拟结果

影响高压扭转成形的工艺参数有：x1,温度;x2,压力;x3,扭转角速度;x4,摩擦因子。粉末锥形件成形的目标是在获得较大致密度的情况下,密度分布尽量均匀,因此选取2个优化指标：平均相对密度ρavg、最小相对密度ρmin,2个指标越大越好。

将上述4个工艺参数作为设计变量,以平均相对密度和最小相对密度为目标函数,建立正交试验设计方案,安排四因素四水平正交表L16,进行16次有限元数值模拟,仿真结果见表1所列。

表1 正交试验方案及模拟结果

4 灰色系统理论多目标优化

4.1 目标函数灰色关联系数及关联度

按照灰色系统理论,将模拟结果按(1)式对2个目标函数分别进行关联系数计算,获得灰色关联系数见表2所列。

考虑单目标函数的最大值为优化目标,将获得的灰色关联系数代入(2)式,计算获得目标函数的关联度见表2所列。

4.2 多目标灰色关联度分析

由灰色系统理论可知,关联度越大,它所对应的目标序列越接近最优值,对目标函数的优化值响应越大[10]。计算各个因子各个水平的平均关联度,结果见表3所列。由表3可知,对灰色关联度影响最大的参数分别是：x1为600℃,x2为700 kN,x3为0.09 rad/s,x4为 0.3,它们是优化的工艺参数组合。

4.3 仿真验证

用上述分析得到的优化成形工艺参数组合进行模拟验证,结果如图3所示,采用统一的相对密度标尺,是为了更清晰地比较优化前后的密度分布。由图3可以看出,优化前平均相对密度为0.978,最小相对密度为0.762;优化后的平均相对密度为0.982,最小相对密度为0.787。由模拟结果可以看出,优化后的平均相对密度得到提高,密度分布均匀性较优化前有显著改善。

表2 目标函数的灰色关联系数及关联度

表3 自变量对目标函数的平均关联度

图3 锥形件子午面相对密度分布云图

5 结 论

(1)本文采用MSC.Marc软件能较好地模拟粉末锥形件高压扭转成形过程,得到了相对密度的分布规律。

(2)基于灰色系统理论,通过计算分析多个目标函数的关联系数、关联度及各个工艺参数的平均关联度,得到了多目标优化的钼粉锥形件压扭成形工艺参数的最优组合。

(3)运用优化的成形工艺参数组合进行了仿真验证,结果显示平均相对密度提高,分布也更加均匀,说明这种方法在粉末压扭成形设计中具有应用前景。

[1]M ackerle J.Finite element analy sis and simulation of powder material,metallurgical process and product[J].Journal of Materials P rocessing Technology,2003,133：378-397.

[2]李 健,张文超.基于有限元模拟的钼粉末温压成形分析[J].稀有金属材料与工程,2009,38(4)：659-662.

[3]王 毅,姜 炜,刘宏英,等.粉末药型罩材料及其工艺技术的研究进展[J].功能材料,2007,12(5)：555-559.

[4]Krasilnikov N A,Sharafutdiniv A.High strength and ductility of nanostructured Al-based alloy,prepared by high-pressure technique[J].Materials Science and Engineering,2007,A463：74-77.

[5]薛克敏,王 真,吕 炎.扭压变形的准三维刚塑性有限元分析[J].塑性工程学报,1997,4(1)：9-13.

[6]薛克敏,张 君,李 萍,等.高压扭转法的研究现状及展望[J].合肥工业大学学报：自然科学版,2008,31(10)：1613-1616.

[7]李 琦,李 萍,薛克敏,等.高压扭转对ZoCrMnTi组织和力学性能的影响[J].合肥工业大学学报：自然科学版,2010,33(9)：1304-1307.

[8]Huang S J,Chiu N H,Chen L W.Integration of the grey relational analysis with genetic algorithm for software effort estimation[J].European Journal of Operational Research,2008,188(3)：898-909.

[9]Shima S,Oyane M.Plasticity theo ry for porous metals[J].Int J Mech Sci,1976,18(6)：285-292.

[10]赵茂俞,薛克敏,李 萍.基于灰色系统理论的铝合金覆盖件成形优化模拟[J].农业机械学报,2008,39(10)：207-210.