模具型腔高效加工的分片轨迹规划研究

黎 振，孙丽杰，蔡玉俊，潘 鑫

（天津工程师范学院 高速切削与精密加工重点实验室，天津 300222）

模具型腔高效加工的分片轨迹规划研究

黎 振，孙丽杰，蔡玉俊，潘 鑫

（天津工程师范学院 高速切削与精密加工重点实验室，天津 300222）

为了实现模具型腔的高效数控加工，提出了一种基于切削带宽方向分区的轨迹规划方法。该方法先将参数曲面进行离散，然后求出各离散点的任意切削带宽方向与带宽大小的关系函数；在UV参数图上表示出此点在取得最大切削带宽条件下的带宽方向，并对离散点的带宽方向进行聚类划分；分片后，根据切削带宽的方向对各分片区内首条加工轨迹进行优化；进而使用等残留高度轨迹规划方法，生成模具型腔精加工的刀具轨迹。仿真证明，该方法能有效地提高加工效率。

模具型腔；带宽函数；路径规划；等残留高度

随着产品更新换代的加快，用户对模具的要求是高质量、短工期、低成本，但模具型腔型面大多采用复杂曲面，给刀具轨迹的规划带来了极大的难度。因曲面区域的性态各不相同，而加工时往往统一对待，这极大地影响了加工效率及表面质量。另一方面，由于轨迹规划方法缺少有计划的使用，使得加工效率没有达到最佳。型腔曲面加工中常用的轨迹生成方法有等参数线法、截面线法、等残留高度法等[1，2]。在这些方法中，等残留高度法是通过控制相邻轨迹间的距离使得轨迹间的残留高度不变，从而在已知一条加工轨迹、刀具半径和允许残留高度的前提下，下一条刀具轨迹便可以计算出来[3，4]。因此，初始路径的选择对刀具轨迹总长度有重要影响，轨迹路径上刀位点的确定都是根据此点曲面局部条件所允许的最大行距计算得到的，所以等残留高度方法是一种高效的加工方法。而实际使用等残留轨迹规划方法加工时，首条轨迹选择的优劣决定了等残留高度轨迹规划方法效率的高低。针对以上问题，本文依据曲面上点的切削带宽函数进行首条加工轨迹优化，进而使用等残留高度轨迹规划方法的加工策略，提高了加工效率。

1 切削带宽函数

曲面上每一点，根据其曲面状况及设定的残留高度，在不同的走刀方向上切削带宽是不同的。设p=s（u，v）为目标曲面的参数方程，其第一、第二基本量矩阵A和B可表示为：

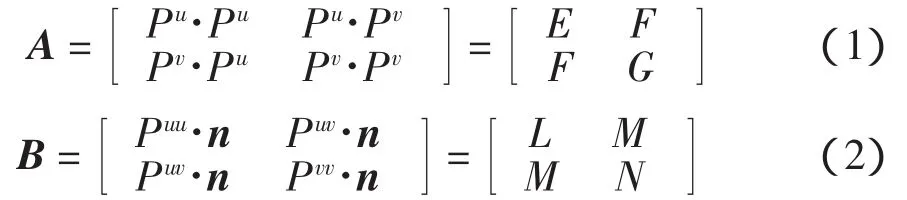
其中：Pu和Pv分别表示曲面沿方向u和v的一阶偏导数；Puv和Pvv表示曲面沿方向u和v的二阶偏导数；n表示曲面的单位法向量。从而曲面的第一、第二基本齐式可表示为：

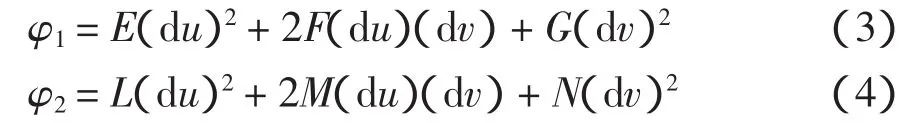
同时曲面各点的高斯曲率K与平均曲率H也可求得：

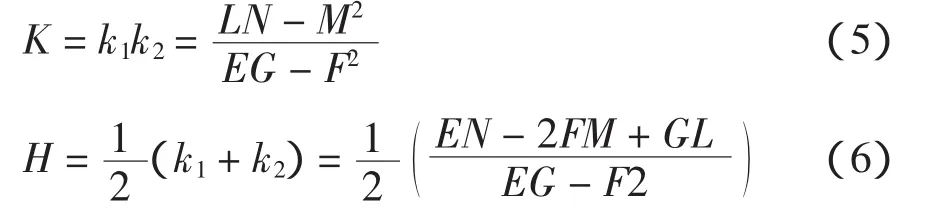
其中，k1和k2是两个主曲率，且k1＞k2。

进而两个主曲率可由（5）和（6）联立解得：

令P0=S（u0，v0）为当前切削点，向量[du，dv]表示在参数平面内的切削方向，相应地，向量[du*，dv*]表示在参数平面内带宽方向，显然这两个方向互相垂直。对给定的残留高度值h，可用下列公式计算出满足精度要求的带宽，即有效带宽：

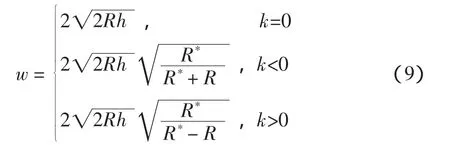
式中：k表示沿[du*，dv*]方向的法曲率表示相应法曲率半径；R为刀具半径。

通过欧拉公式，可以求任意[du*，dv*]方向上的法曲率：

在k1和k2两个主曲率中，k1＞k2，ω是 [du*，dv*]方向与k1对应主曲率方向的夹角。由以上公式可知，要让有效带宽达到最大，[du*，dv*]须沿k1对应主曲率方向，即当前切削方向必须沿着k2对应的主曲率方向。

在参数平面内，以当前切削点P0=S（u0，v0）为极点，以k2对应的主曲率方向为极轴，建立极坐标系，在此坐标系内建立有效带宽w与切削方向角θ的函数：

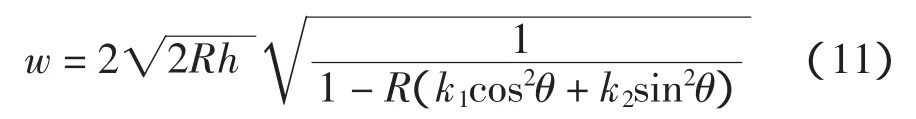
这里的θ是切削方向与k2对应的主曲率方向的夹角。此函数在极坐标系内的表达如图1所示，其中极径最大的方向即为有效带宽最大的切削方向。

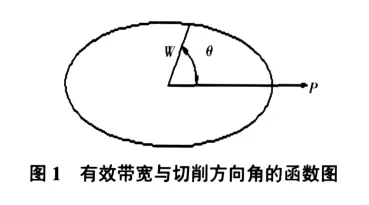
2 切削路径的规划

对给定的当前切削点，残留高度一定，最优的切削方向即为切削带宽最大的方向。曲面上的所有点，都可以根据式（11）得到切削带宽图（见图2）。保证在曲面片上每一点的切削带宽最大的方向为局部最优的切削方向，可得到曲面的最优的切削带宽方向图谱，如图3所示。

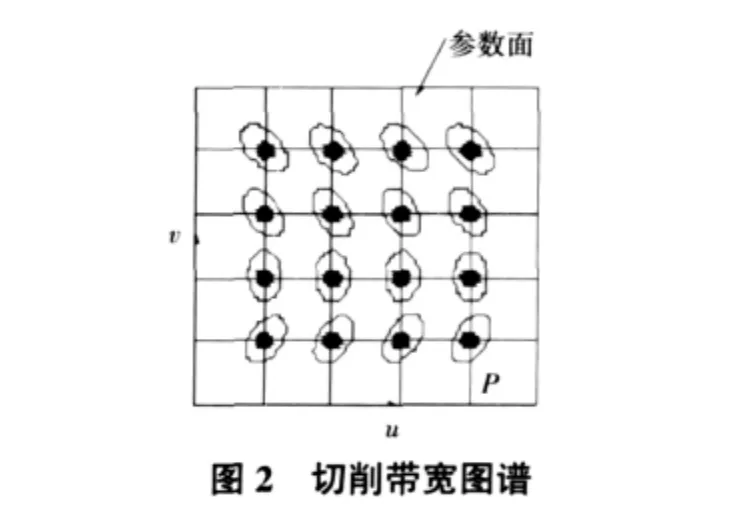
从图3可以看出，各个点在最佳带宽的条件下切削方向近似平行于v轴。因此，在对该区域使用等残留高度轨迹规划方法进行路径规划时，选取v轴所在的边为起始路径进行路径规划效率是最高的。

2.1 短程线理论

等残留高度的主要理论依据是短程线理论。根据微分几何理论可知，曲面上不在边界上的足够接近的两点的短程线是曲面上这两点之间弧长最短的连线。且过曲面上任一点的任一方向，总有唯一一条短程线。要保持残留高度值不变，则两切削行的间距就应该在短程线上根据曲面行距方向的法曲率半径来调整[5，6]。残留高度h是两切削行的间距与沿行距方向的法曲率半径Rn的函数。如果要保持残留高度的不变，必须根据沿行距方向的法曲面半径Rn来调节行距[3，7]。

设加工曲面的参数方程表示为：

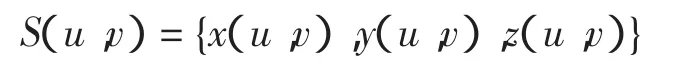
首先假设一条已知刀具轨迹线为C（u（t），v（t）），P0为曲线上一个刀位点，根据短程线曲率半径求其相邻等残留点P*，如图4所示。

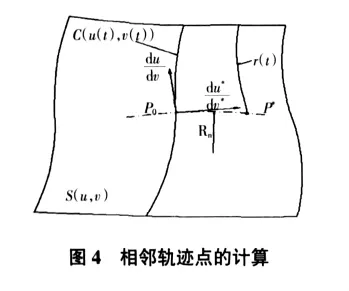
由短程线的几何性质可知，曲线上的给定点处的短程线的主法矢方向是沿着曲面在该点的法矢法向。根据曲面的第一和第二基本齐式可以得到短程线的曲率半径为：

式中，Ⅰ、Ⅱ分别为第一和第二基本齐式，表示如下：

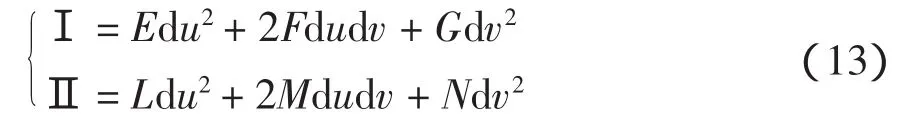
式中，E、F、G为曲面第一类基本量，表示如下：

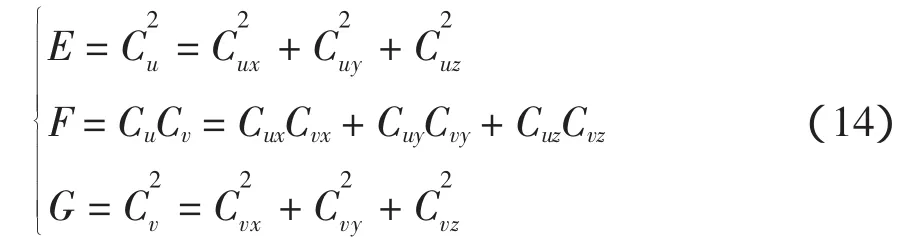
L、M、N为曲面第二类基本量，表示如下：

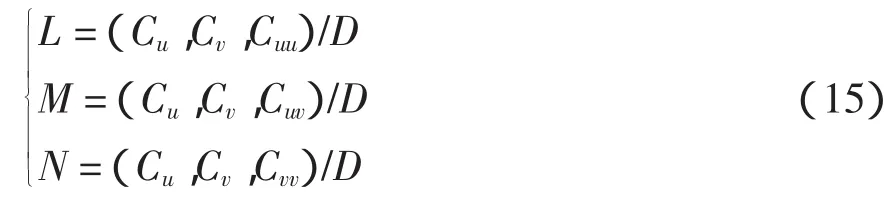
在图4中，沿短程线方向的第一和第二基本齐式为：

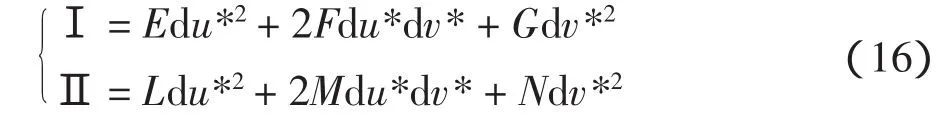
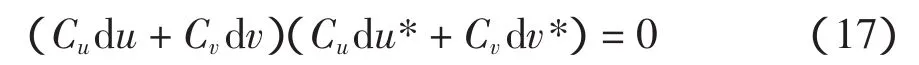
这也就是定义了垂直于轨迹切线方向的短程线方向。通过化简可得到

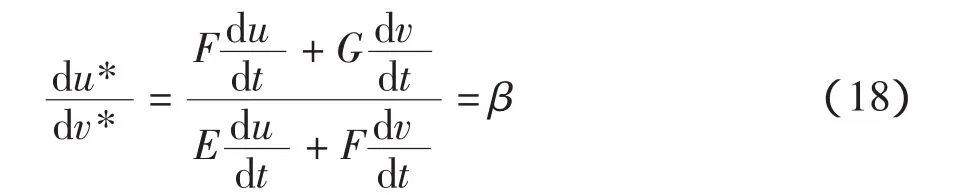
将上式代入式（12），得短程线曲率半径Rn为：

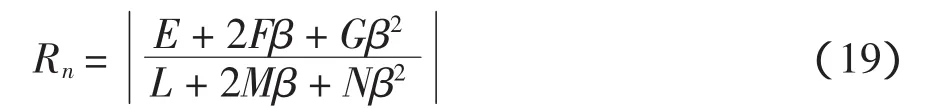
2.2 切削行距的计算

切削行距是按刀位计算点所在的局部曲面的曲率大小分情况讨论计算的。局部曲面的曲率有R*=0（平面），R*＞0（凸曲面）和（凹曲面）R*＜0三种类型，不同的曲面类型采用不同的行距计算公式[3]。

设R为刀具半径，h为残留高度，Rn为已知刀位点沿短程线方向的曲率半径。

那么，当局部曲面为平面时，行距L计算公式为：

当局部曲面为凸曲面时

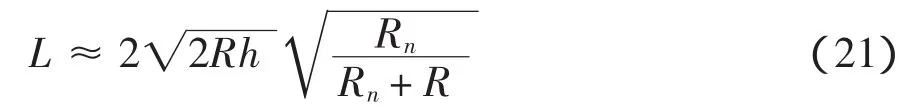
当局部曲面凹曲面时

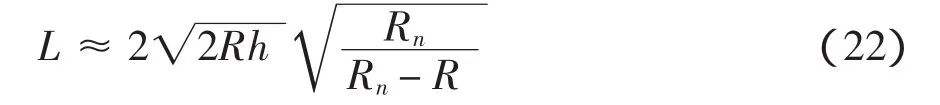
2.3 相邻等残留轨迹点的计算

设已知刀具轨迹线为P（u（t），v（t）），P0为此条轨迹线上的某一已知刀位点，那么可求出在短程线方向上切削步距为L的相对应的相邻等残留轨迹点P*。

由于P0和P*必须满足方程：

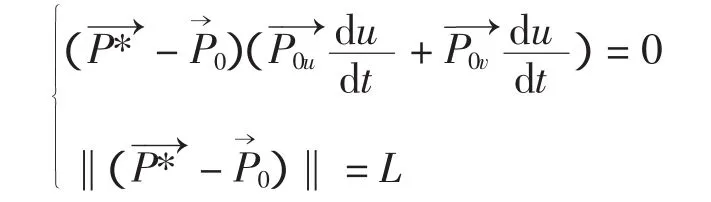
通过泰勒展开及化简可得：

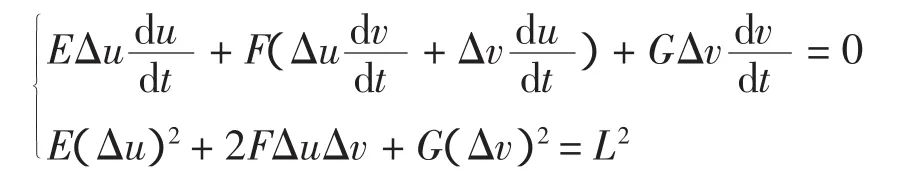
求解上述方程组，可得到：

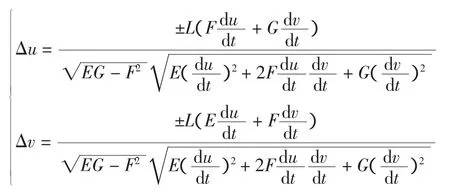
在求得的Δu、Δv解中，正负号需要根据加工方向来确定。

3 仿真实例

图5所示为一模具型腔，曲面由四个相似的曲面片拼接而成，在连接处曲率较大。设定表面加工精度为0.05 mm。

首先，对曲面进行参数离散，求出各离散点的切削带宽，据最大切削带宽求出各点的局部最优切削方向，局部最优切削带宽对曲面进行聚类分片，分区如图6所示。

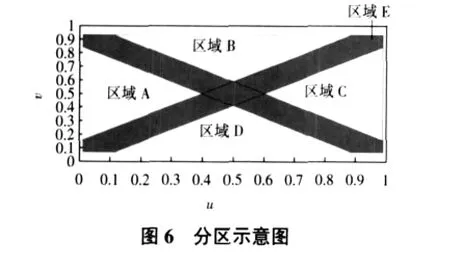
在A、B、C、D四个区域，最优切削方向各不相同，但在各区域内部大致相同，因此在A、C区域内部，以v向作为初始刀轨，在B、D区域内部，以u向作为初始刀轨，采用等残留高度法加工，可大大提高效率。根据局部最优切削带宽确定加工路径，由所给定的刀具及残留高度h，根据有效带宽与切削方向的关系，分别对各区域采用不同的首条轨迹方向进行等残留轨迹规划，如图7所示。对于区域之间的过渡区域E，因过渡在圆角处，采用小刀具进行清根操作。

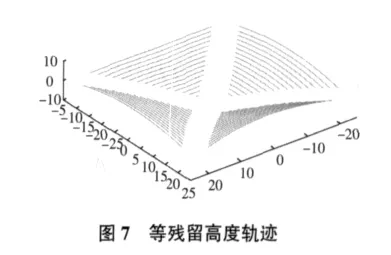
根据以上轨迹规划的方案，采用φ10球头铣刀加工，得到整个区域内的轨迹线总长为1 216.8 mm。传统轨迹规划直接以x轴为边界线进行等残留轨迹规划，区域内轨迹线总长在1 871 mm以上。效率提高约30%，新方案的优势明显。

4 结论

本文提出的数控加工的分片轨迹规划方案，根据曲面切削带宽方向的不同，聚类分区划分，利用切削带宽函数在各区域内选择最优的首条轨迹，进而使用等残留高度法进行轨迹规划，充分利用了切削带宽函数。从计算实例可以看出，这种方法能有效地提高加工效率。

［1］ SURESH K，YANG D C.Constant scallop-height machining of freeform surfaces[J].ASME Journal of Engineering for Industry，1994，116：253-259.

［2］ AGRAWAL R K，PRATIHAR D K，CHOUDHURY A R. Optimization of CNC isoscallop free form surface machining using a genetic algorithm[J].International Journal of Machine Tools&Manufacture，2006，46：811-819.

［3］ LEE Y S，MA Y，JEGADESH G.Rolling-ball method and contour marching approach to identifying critical regions for complex surface machining [J].Computers in Industry，2000，41：163-180.

［4］ CAI YJ，DUANCJ.Astrategyoftoolpath generation for finish machining of mold cavity based on tool-zmap model[J]. Progress ofMachiningTechnology，2009（407/408）：273-278.

［5］ CHIOU C J，LEE Y S.A machining potential field approach to tool path generation for multi-axis sculptured surface machining[J].Computer-Aided Design，2002，34：357-371.

［6］ KOKH T，MAEKAWANM.Patrikalakis An algorithmfor op timal free-form object matching[J].Computer-Aided Design, 2003，35：913-923.

［7］ ALAN C L，LIN H T.Automatic generation of NC cutter path from massive data points [J].Computer-Aided Design，1998，30：77-90.

Research on patched NC planning for high-efficiency machining of mold cavity

LI Zhen，SUN Li-jie，CAI Yu-jun，PAN Xin
（Tianjin Key Laboratory of High Speed Cutting&Precision Machining（TUTE），Tianjin 300222，China）

In order to achieve efficient machining for mold cavity,the patched NC planning method is presented in this paper，which is based on the direction of cutting bandwidth.Firstly the parametric surfaces are discretized，then relative function of each discretized points between the direction of arbitrary cutting bandwidths and size of bandwidth is found，and the bandwidth direction of this point under achieving maximum cutting bandwidth on the UV parameters surface are shown.Finally，the direction of discrete points′bandwidth can be divided into cluster.For each patched surface，the first machining toolpath of each sub-area according to the direction of cutting bandwidth is optimized.Further，toolpath of mold cavity maohining can be obtained by using the iso-scallop height planning method.The simulation shows that the method can realize more efficienct NC machining for mold cavity.

mold cavity；bandwidth function；toolpath planning；iso-scallop height

book=1,ebook=7

TG76

A

1673－1018（2010）01－0015－04

2010-01-20

国家自然科学基金资助项目（50975203）；天津市自然科学基金重点项目（08JCZDJC18400）.

黎 振（1978—），男，硕士，研究方向为CAD/CAM.