RS编译码电路的可重构性研究
2010-08-29谭思炜潘红兵龙宏波
谭思炜, 潘红兵, 龙宏波
(海军工程大学电子工程学院,武汉 430033)
0 引言
可重构性是指同一系统的硬件或软件模块根据数据流或控制流的输入重新配置,改变电路结构或模块功能,满足新的任务需求。目前可编程集成芯片大规模运用在通信系统设计领域,给可重构电路的实现带来可能。本文根据集成芯片的可编程特点,以可重构的思想对传统的编译码电路进行修改,使其能依据不同通信系统RS(Reed-Solomon)码标准的配置信息,实现对应的编译码过程。
RS码是定义在伽罗华有限域G(2m)上的一种多进制BCH码,具有较强的纠错能力,构造方便,易于实现。但针对于不同的通信系统,RS码的标准不尽一致。常用到的RS码标准有:数据系统顾问委员会(CCSDS)的RS(255,233)、数字电视传输系统(DVBS)的RS(255,239)或RS(204,188)、光存储技术中DVD的RS(208,192)或RS(182,172)以及高清晰电视(HDTV)RS(255,235)或RS(207,187)。因而实际工程应用中需要根据对应的编码标准设计RS编译码器。显然,如果需要编译码电路具有可重构性,满足以上几种常用的编码标准,则只要编译码器的码长满足最大值255,可纠正错误符号位数为最大值11即可。
1 可重构RS编码电路
得其具有较强的突发纠错能力。定义2t=n-k,t表示RS码是由生成多项式G(x)定义的一组线性循环码RS(n,k),k表示数据符号码长,n表示包括数据符号和校验符号在内的码长。RS码非二进制的属性使RS码的纠错能力,即最多纠正t个符号的错误。
RS编码过程一般可以表示为:C(x)=I(x)+(I(x)◦x2t)mod G(x)[1],其中C(x)表示码字多项式,I(x)表示数据符号多项式。显然一组RS码是由两部分组成,前面k位是符号码,后面的n-k位是校验码,校验码是通过数据符号与生成多项式通过多项式的长除求余得到的。因而校验码的计算就是编码的主要过程。
硬件上一般采用线性反馈位移寄存器(LFSR)实现以上计算过程。如图1所示,向LFSR依次输入信息码,同时信息码流向输出端,经过k次位移,信息码输入完毕,多项式的长除也计算完成,寄存器内得到余数,即校验码。最后依次输出寄存器内的校验码,输出端即可得到码长为n的RS码。这里涉及到的运算都是有限域内的乘法和加法。
由图1可知,LFSR中寄存器个数N是由RS的纠错能力t决定的,N=n-k=2t。设法改变N值,即可满足不同t值的RS编码标准。通过配置信息将N值输入到可重构RS编码电路,从而得到相应标准的编码器。由于讨论的标准中2tmax=22,故设置22个寄存器的RS编码电路。其可重构电路如图2所示。

图1 RS编码电路Fig.1 RSencoding circuit
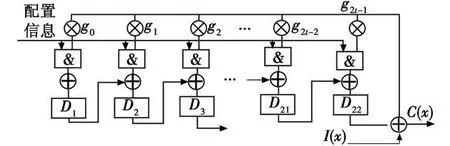
图2 可重构RS编码电路Fig.2 A configurable RS encoding circuit
如果需要配置的寄存器个数小于22个,则配置信息逐位设置0或1从左往右通过依次关掉与门来关掉不需要的寄存器,直到剩下的寄存器组可以构成对应标准所需的LFSR为止。
2 可重构RS译码电路
RS码的译码过程主要包括伴随式的计算、解关键方程以及纠错。其中最关键的步骤在于解关键方程。目前解关键方程的算法很多,本文采用改进的欧几里德算法,求得错误位置多项式和错误值多项式,利用钱氏搜索得到错误位置,然后运用Forney算法计算错误值,最后求和纠错,从而完成整个译码过程。
2.1 可重构伴随多项式计算
设译码端接收到的码字多项式为R(x),则有R(x)=C(x)+E(x),其中E(x)表示信息在信道中由于噪声干扰或衰落产生的误码,同样以误码多项式表示。伴随多项式S(x)可以直接从接收码字多项式中计算得到,定义伴随多项式见式(1),其系数个数为
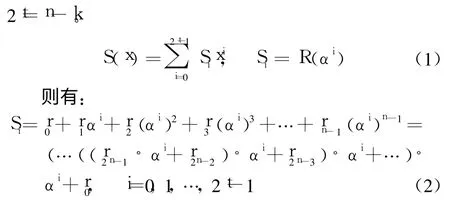
由式(2)可知,求伴随多项式符号Si的过程可以通过有限域内的乘法和加法迭代运算实现,如图3所示。将Si的计算设为若干相同的独立模块,并行执行,即可得到各个伴随多项式的系数。这里同样设置伴随多项式符号个数最大值2tmax=22,根据编码标准,输入配置信息打开相应个数的伴随多项式符号计算模块,输入接收码字和与各Si模块对应的符号αi,完成伴随多项式系数的计算,如图4所示,即可满足任意标准RS(n,k),n-k≤22的伴随多项式计算。
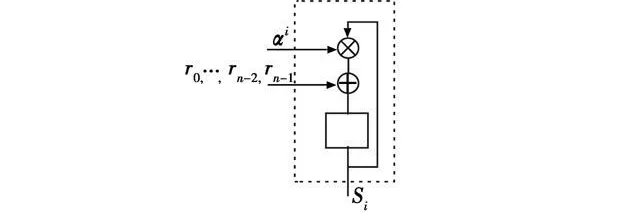
图3 Si迭代计算模块Fig.3 Siiterative computation block
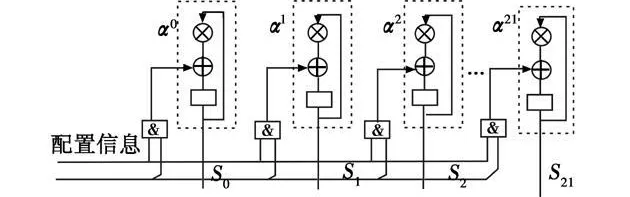
图4 可重构伴随多项式计算电路Fig.4 Reconfigurable syndrome computation circuit
2.2 关键方程求解
定义错误位置多项式:
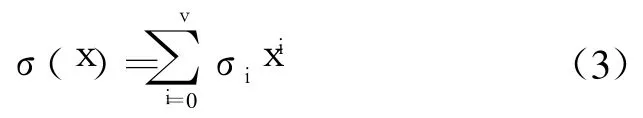
其中:v表示错误个数。错误多项式是用来定义某位接收码字上的错误,显然v≤t,表示错误个数应该在RS码的纠错范围内。如果rk上发生错误,则有σ(α-k)=0。
定义错位值多项式:
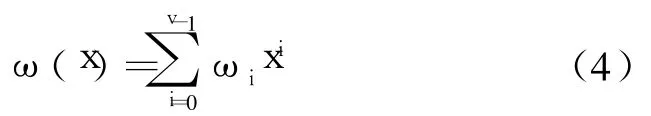
错误位置多项式σ(x)和错误值多项式ω(x)可由伴随多项式S(x)通过如下方程求得:
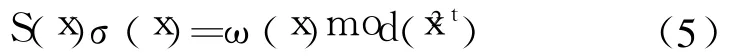
方程(5)称为关键方程。改进欧几里德算法[2]的迭代过程如下所示。
1)初始化。

其中:ai-1,bi-1分别表示Ri-1(x),Qi-1(x)的首项系数。显然式(7)、式(8)的迭代运算相同,因此可用图5所示的运算模块实现,每迭代一次就需要一个运算模块,迭代次数i≤v,v为错误个数。所以可在译码器电路里预先设置t个迭代运算模块,以满足不同标准的RS码译码运算,实现其可重构功能。解关键方程的可重构电路结构如图6所示。
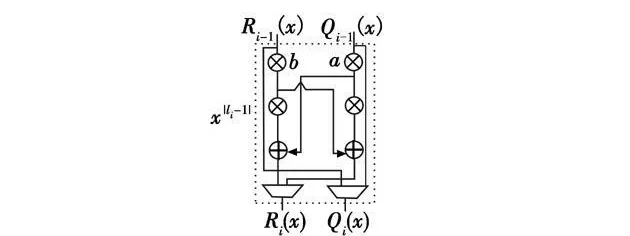
图5 改进欧几里德迭代运算模块Fig.5 Iterative computation block of modified Euclidean algorithm

图6 解关键方程的可重构电路结构Fig.6 Reconfigurable key equation circuit
2.3 钱氏搜索与纠错
由错误位置多项式的定义可知,只要逐位判断σ(α-k)=0,k=0,1,…,n-1是否成立,即可知道接收码字的正误。所以需要逐位计算σ(α-k),这就是钱氏搜索[3]。
码字的纠错使用的是Forney算法[6],利用关键方程求解得到的错误位置多项式σ(x)和错误值多项式ω(x)计算并纠正错误。其算法如下[5-10]:
即求出σ(α-k)的偶数项,用其倒数与ω(α-k)相乘,完成Forney算法中的除法运算。倒数运算可以用查表法实现。显然σ(α-k),oddσ(α-k)和ω(α-k)都是多项式的运算,因而可以用与式(2)相同的方法迭代实现。迭代模块与图3的伴随多项式迭代计算模块相同,这里不再复述。需要指出的是oddσ(α-k)的计算需要依次向迭代模块输入错误位置多项式σ(x)的奇数项系数,奇数项系数的获得可以通过选择器在σ(x)系数输入的同时选择其奇数项系数,输入到oddσ(α-k)的迭代模块,具体实现方法如图7所示。
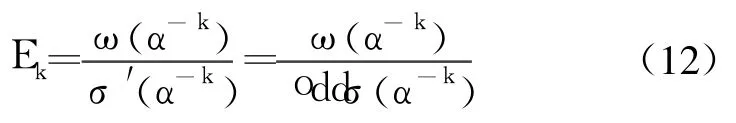
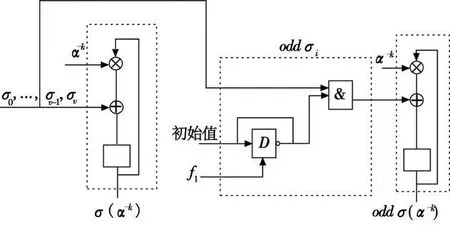
图7 σ(α-k)和oddσ(α-k)计算模块Fig.7 σ(α-k)and oddσ(α-k)computation block
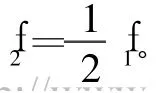
错误值计算模块如图8所示,判断计算得到的σ(α-k)是否为0。如果发生错误,则选择用Forney算法计算的错误值,否则多路复用器输出0。最后将错误值与缓存中的接收码求和即可纠正错误。
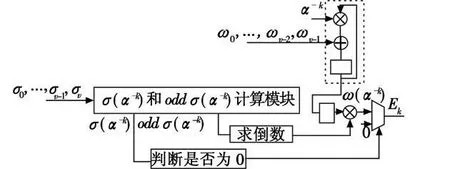
图8 错误值计算Fig.8 Error value computation
错误值计算的可重构结构如图9所示,设错误值计算模块个数为255,并行计算n位接收码的错误值,提高计算速度。根据不同RS码标准,输入配置信息,选择相应数量的错误值计算模块。
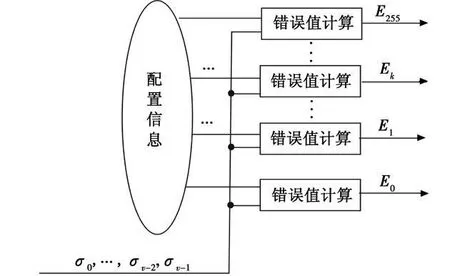
图9 错误值计算的可重构结构Fig.9 Reconfigurable error value computation structure
3 结论
本文介绍了RS码的编译码原理与过程,讨论了编译码电路结构,并提出了具有可重构特性的硬件实现电路。该可重构结构以RS(255,233)标准为参考对象,并向下兼容所有码长小于等于255,可纠错的符号位小于等于11的RS编码标准,应用范围广。但RS(n,k)的n及n-k值越小,电路硬件的使用率越低,因而适合n,n-k值较大的RS编码标准。电路中使用的多项式迭代计算模块相同,如Si,σ(α-k),oddσ(α-k)和ω(α-k)的计算,因而适合RS编译码电路的大规模集成。在计算速度方面,编译码电路中的迭代模块以一组RS码输入时间为一个计算周期,并行计算的伴随多项式系数和错误值,将传统的编译码电路的对应模块计算时间分别缩短为1/2t和1/n。相对于传统的编译器,本文提出的可重构编译码电路只是在其基础上增加了4t+n个与门,加法器乘法器的开销增加了2t+n-2,但其可重构性使其可成为常用RS标准的通用编译码器。
[1]王新梅,肖国镇.纠错码—原理与方法[M].西安:西安电子科技大学出版社,2006.
[2]LEE M H,CHOI S B,CHANG J S.A high speed Reed-Solomon decoder[J].IEEE Transactions on Consumer Electronics,1995,41(4):1142-1148.
[3]HSU H Y,YEO J C,WU A Y.Multi-symbol sliced dynamically reconfigurable Reed-Solomon decoder design based on unified finite field processing element[J].IEEE Transactions on Very Large Scale Integration Systems,2006,14(5):489-499.
[4]McELIECE R.The theory of information and coding[M].2nd ed UK:Cambridge University Press,2002.
[5]HSU H Y,WANG SF,WUA Y.A novel low-cost multimode Reed-Solomon decoder design based on Peterson-Gorenstein-Zierler algorithm[J].Journal of VLSI Signal Processing,2003,34:251-259.
[6]CHAARI L,FOURATI M,MASMOUD N,et al.A reconfigurable FEC system based on Reed-Solomon codec for DVBand 802.16 network[J].WSEAS transaction on circuits and systems,2009,8(8):729-744.
[7]SONG Leilei,YU Meilin,SHAFFER M S.10and 40Gb/s forward error correction devices for optical communications[J].IEEE Journal of Solid-State Circuits,2002,37(11):1565-1572.
[8]李伟.面向序列密码的反馈位移寄存器可重构并行化设计技术研究[D].郑州:解放军信息工程大学,2009.
[9]张天喻.基于改进型欧几里德算法的RS译码研究[J].齐齐哈尔大学学报,2009,25(1):1-5.
[10]张怡,韩维.高速RS编码算法及FPGA实现[J].无线电通信技术,2005(1):23-26,30.
