电视制导导弹无线电指令加密认证研究
2010-08-27王燊燊冯金富
王燊燊, 冯金富, 李 骞
(空军工程大学工程学院,西安 710038)
0 引言
机群作战时,若载机吊舱与电视制导导弹之间的通讯频率和指令的编码方式相同,不同载机发射的两枚导弹的无线电指令信号会相互干扰,为了能同时攻击邻近目标需要克服指令间的干扰。通常采用单层密钥的分组密码对导弹的控制指令进行加密,这种方法密钥空间较小,难以抗击指令干扰和敌方的主动干扰。为克服这两方面的干扰,本文提出了一种含有载机认证的无线电控制指令编码加密方案。
1 指令传输模型
电视制导导弹[1-2]控制指令由编码组件进行编码,在发射机内进行 AM调制,调制后的信号放大后经天线发射出去。导弹由导弹尾部天线接收控制指令信号,除有用信号外,还有干扰信号。干扰源可能是敌人积极干扰,也可能是外界噪声。导弹上的接收机采用非相干解调,解码组件对接收到的信号进行解码。为保证制导指令的保密性和真实性,需要在指令传输过程中增加加密认证模块。增加加密认证模块后制导指令的发射与接收过程如图 1所示。
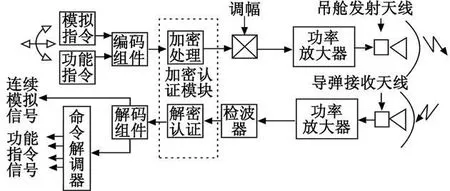
图1 制导指令的发射与接收过程Fig.1 Sending and receiving process of guidance command
由电视指令制导导弹的工作过程[3-4]可知,控制信息分为两大类:一次性功能指令和连续模拟信号。在这里采用分组码得到 8位的二进制数字序列表示一次性功能指令,两路模拟信号由 A/D转换器转换成 7位二进制码,第 8位为奇偶校验位。因此明文序列为24位的二进制码序列。
2 非线性滤波函数
在加密方法中,对多个 LFSR输出进行非线性函数变换后产生密钥序列,为使非线性变换中序列密码的良好统计特性不被破坏,在构造非线性组合函数时必须依据一定的准则,为此函数生成相当困难[5-6]。本文利用离散 Hopfield神经网络对 LFSR的当前状态按网络的稳定点进行分类,然后设计一个 S盒使神经网络的输出一半对应 0,一半对应 1,从而生成随机序列,这样既能使得该序列某些统计特性不被破坏,又能利用离散 Hopfield神经网络[7]模拟复杂的非线性输出函数,起到非线性系统作用。
一般情况下,非线性滤波函数 f是平衡的非线性布尔函数。设为基于二进制域 F2的 n维向量空间。布尔函数 f(X)=f(x1,…,xn)是到 F2的映射(其中 F2是 0,1两个数对模 2加和模 2乘运算构成的域,数学上叫做枷罗华域,表示二元枷罗华域上的 n维向量空间),具有平衡性准则,要求组合函数 f的输出值中 0与1的数目各占一半,它是f具有伪随机性的必要条件[8]。方案设计的思想是利用神经网络的收敛特性构造一个 S盒进而组成组合非线性滤波函数 f输出随机序列。
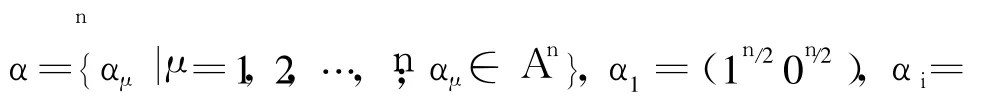
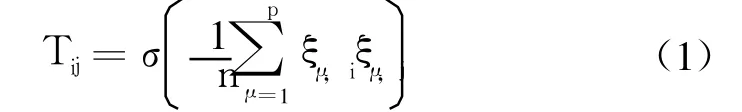
函数 σ(·)定义为
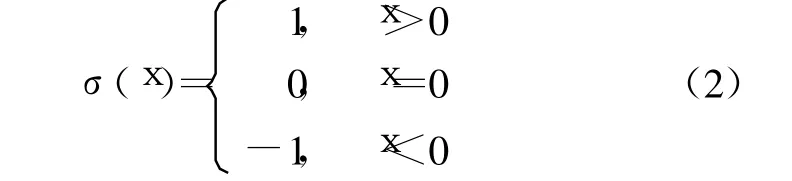
用矩阵的形式表示为
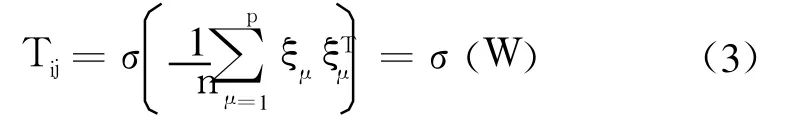
突触权值被确定为 3种状态:-1,0,1。这种网络有利于硬件(DSP)实现。这种网络必须采用同步方式,因为每次只有一个神经元进行更新,而且达到稳定状态步数一般情况下也是未知的。网络的动力学方程为
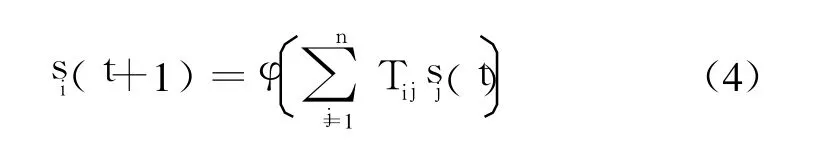
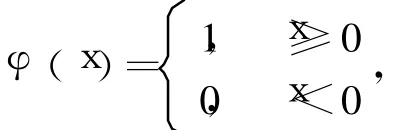
在本文所设计的方案中取 n=8,一组 16个的存储模式 {α,β}定义为

当网络由吸引点 {α,β}确定时 ,设 Λαi和 Λβi分别表示吸引点 αi和 βi吸引状态向量的个数,穷举 8维向量空间得到 Λαi,Λβi,如表 1所示 。
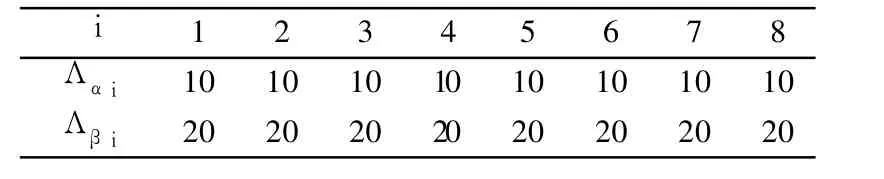
表 1 稳定点 αi和 βi的吸引域Table 1 Attractive field ofαi andβi
由上面可以得知,8个神经元的网络能够将 16个8维向量作为稳定点。由于在 8维向量空间中,大多数的状态向量都能收敛于 8个稳定点中的一个。因此定义网络的记忆过程为的映射,函数 Γ的输入是一组 n维向量,输出为 Θ={α,β,τ},其中 α,β是如上所示的一组 2n个稳定点,τ为网络的伪状态,这时系统出现限幅的自恃振荡或极限环。
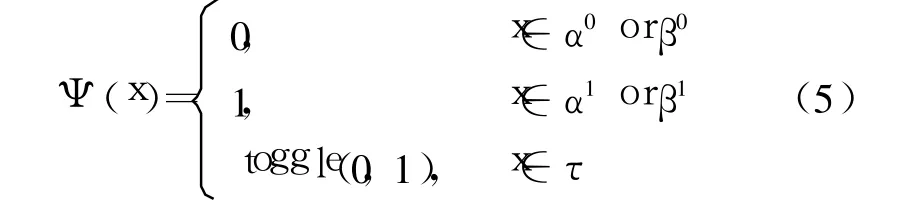
当 x属于 α0和 β0时,Ψ为 0;当 x属于 α1和 β1时,Ψ为 1;当 x属于 τ,“0”或“1”被轮流输出。这样,得到一个平衡的映射。
3 指令加密和认证方案
结合对称密码与非对称密码[9]的特点,考虑到飞机与导弹是一对多的关系,因此可以采用对称密码与非对称密码相结合的方法来实现制导指令的加密和认证。每架飞机具有一对公私密钥对,设公钥为 KU,私钥为 KR,密钥对由机载计算机产生,其中私钥为飞机所独有,而公钥在导弹发射前由飞机传输给导弹。这样飞机的公钥也只有导弹知道,即飞机的公钥与私钥对外界都是保密的。每次通信前由飞机产生一个随机的对称密钥 K,或称会话密钥,用于对指令进行加密。载机吊舱对指令的加密处理过程如图 2所示。
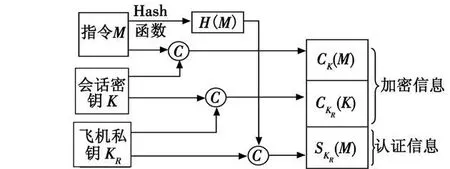
图 2 载机吊舱的加密处理Fig.2 Encryption process of pod
设载机上的吊舱欲发送给导弹的指令是 M,吊舱发送指令前进行如下处理:1)使用会话密钥 K对指令M进行加密得到密文 CK(M),其中 CK([])是密钥控制的函数;2)用飞机私钥 KR对会话密钥 K进行加密得到密钥密文计算指令 M的 Hash值H(M),并用飞机私钥 KR对校验码 H(M)进行加密得到飞机对指令的数字签名然后向导弹发送导弹上存有飞机公钥 KU,当收到吊舱发来的消息后,进行如下处理:1)用飞机公钥 KU从密钥密文中解密出会话密钥 K;2)用会话密钥 K从密文CK(M)中解密出明文 M′;3)用飞机公钥 KU从数字签名SKR(M)中解密出原始指令的 Hash值 H(M);4)用相同的算法计算 M′的 Hash值 H(M′),比较 H(M′)和H(M),若相同则认为 M′真实可靠。其处理过程如图3所示。
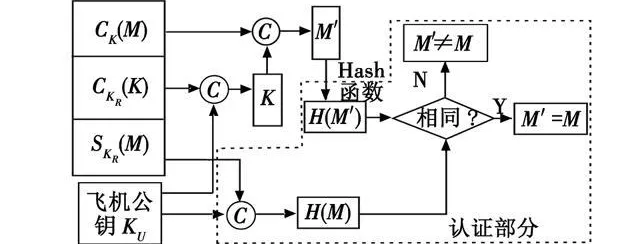
图3 导弹的解密及认证Fig.3 Decryption and authentication process of missile
采用以上加密认证方案实现了以下功能:1)用多重密钥实现了指令信息的保密性,因为指令的保密性依赖于会话密钥,会话密钥的保密性依赖于飞机公钥,而飞机公钥只有导弹拥有;2)导弹相信发送方是发射该导弹的载机,这是因为除飞机外再无其他人知道飞机私钥,因此其他载机不可能对该导弹发送的消息计算出正确的认证码;3)导弹相信发送方发来的消息未被篡改,这是因为攻击者不知道飞机私钥,所以不能在篡改消息后相应地篡改认证码,而如果仅篡改消息,则导弹计算的新认证码将与收到的认证码不同。
明文为 24位的二进制代码,在常用的序列密码中一般使用多个 LFSRi(i=1,2,…,n)的串行输出作为驱动源,LFSRi(i=1,2,…,n)的级数分别为 N1,N2,…,Nn,而且为了使序列周期有尽可能大的周期和计算复杂度,N1,N2,…,Nn两两互素且需要满足一定条件[10]。但在电视指令制导中,考虑明文序列比较短,不需要长周期的序列,而且对反应时间要求比较高,所以仅使用一个 LFSR,在这里采用 8个寄存器的 LFSR,其特征多项式为 p(x)=1+x4+x5+x6+x8,产生了周期为 255的序列,8个寄存器的当前状态将作为初始状态输入给神经网络。当 LFSR的特征多项式确定后,寄存器的当前状态由 LFSR的初始状态决定,这样表示 LFSR的初始状态的 8位二进制码就可以设计为一级密钥。对于线性反馈移位寄存器,考虑到全零状态比较特殊,把它作为电路设计时初始状态,当电路开始工作时,动态地产生一个随机数作为 8级的线性反馈移位寄存器的初始输入,这个初始输入随机数的集合 K就作为会话密钥,范围用二进制表示为[00000001 11111111],元素个数为 255个。会话密钥输入到非线性滤波函数 f=Ψ(Γ(x))就得到密钥流,密钥流和明文经过异或运算后就得到密文。
Hash函数的设计利用纵向冗余校验(LRC)的方法,用来验证指令的完整性。现代密码学中一般使用MD5或 SHA算法作为 Hash函数,但这些算法生成的摘要值普遍偏大,不适合在本系统中使用。纵向冗余校验将位块组成列表,并计算每个列的奇偶校验位[11]。例如,如果二进制数据为 32位,则把其排成 4行,然后对每列计算奇偶位,生成一个 8位的新行,作为整个块的校验位,这样 LRC实际上是初始消息的指印。接收方收到后把数据和 LRC分开,对数据执行LRC运算,并将得到的 LRC值与收到的 LRC值比较,若相同,则相信发来的数据没有在中途发生改变。
非对称密钥的设计利用简化的 RSA方法[11]构造。由于飞机的公钥和私钥对外界都是保密的,因此在采用 RSA算法产生密钥对时,可以采用相对较小的素数代替大素数,即在 RSA算法第一步中选择两个相对较小的质数。这样不会破坏算法的安全性,但能较大地提高算法的运算速度,满足制导指令的时效性要求。这里称这种方法为简化的 RSA算法。由于选择的素数相对较小,密钥对的产生又由机载计算机在导弹发射前完成,因此密钥对的生成不会影响到制导指令的时效性。
RSA算法中大量的运算是方幂模运算,即求 dk(mod r),这里 r为两个大素数的乘积,k在加密时用公钥,解密时用私钥。由于字长的限制,方幂模运算是不能直接进行的,要采用多精度运算,这使得 RSA运算量大,速度慢,因此提高 RSA的速度显得尤为重要。目前有 BR算法,SMM算法,2k进制,montgomery算法等。著名的 montgomery算法是从求余过程中避免除法运算的方面加快方幂模运算,2k进制算法是从缩短指数链,减少迭代次数方面加快方幂模运算,这里采用将大数的幂模运算转化为较小数的求模运算的方法,加快方幂模运算速度,便于硬件实现。
模运算使用函数 f1(d,r)=d(mod r),其中输入为基数 d和模数 r,输出 c=d(mod r),算法描述为
1)设变量 x=d,比较 x与 r;
2)若 x≥r,x=x-r并转到 2),否则转到 3);
3)求模结果 c=x。
上述算法只需简单的加减法即可进行模运算,实现较简单,但它只适合对较小的整数进行模运算。在RSA算法中,加密与解密过程都是对某个数先进行幂运算,然后求模,若先计算求幂结果再进行求模运算,不断多次涉及到大数的乘法,且求模过程运算量大,使运算过程异常复杂,耗费时间长。因此需要设计一种对幂函数的求模方法,以提高运算效率。方幂模运算方法描述如下:
方幂模计算函数 f2(d,k,r)=dk(mod r),其输入为基数 d,指数 k和模数 r,输出 c=dk(mod r),算法描述为
1)设变量 x=d,比较 x与 r;
2)若 x≥r,利用模计算函数 f1求出 x=f1(x,r)=x(mod r);
3)设变量 i=1,s=x;
4)若 i<k,s=s×x,否则转到 7);
5)若 s≥r,利用模计算函数 f1求出 s=f1(s,r)=s(mod r);
6)使 i增 1,即 i++,转到 4);
7)求模结果 c=f1(s,r)=s(mod r)。
上述方法将复杂的幂运算和求模运算转化为简单数的乘法与求模运算,能有效提高 RSA算法加解密效率,便于算法的硬件实现。
4 DSP实现和仿真
带有载机认证的加密方案如图 4所示。
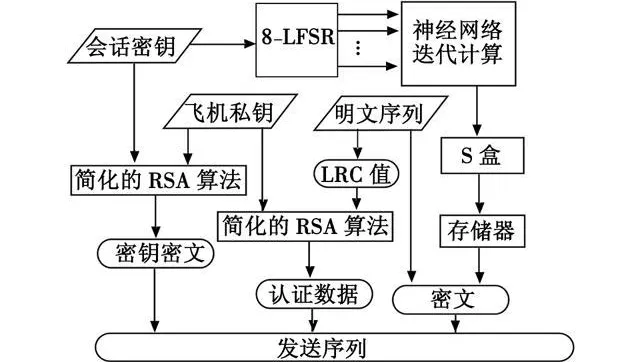
图4 发送序列产生过程Fig.4 Engendering process of sending message
其过程如下所述。
1)设计非线性滤波函数 f,由一个神经网络和一个 S盒。
①设计一个神经网络,选择网络神经元的个数n=8,使得大多数的 8位随机向量收敛到网络的稳定点;
②设计 S盒,满足非线性滤波函数 f的输出一半对应 0,一半对应 1。
2)使用 RSA算法产生飞机的公私密钥对,私钥存储在飞机上,公钥在导弹发射前由飞机传输给导弹。
3)产生明文和随机选择 8-LFSR的初始状态。
4)产生发送序列,包括认证数据、密文和密钥密文。
①由明文的校验码经飞机私钥加密生成认证数据;
②由 m-LFSR的初始输入作为序列发生器的密钥生成密钥流并对明文加密;
③由飞机私钥对 m-LFSR的初始值加密生成密钥密文。
本文在制导指令加密认证方案的 DSP实现方面采用了 TMS320C54x芯片。TMS320C54x芯片是为实现低功耗、高性能而专门设计的定点 DSP芯片,主要应用在无线通信系统和远程通信嵌入式系统中[12]。该芯片速度快,运算能力强,且具有强大的寻址能力。为保证程序掉电后不丢失,需要采用 Flash存储器扩展程序存储区。
在确定系统硬件和处理算法后采用 CCS(Code Composer Studio)集成开发环境来对整个算法和 DSP的运行情况进行仿真[13]。仿真分为两个部分,对吊舱的仿真和对导弹的仿真。设两路连续指令为 11100110、01110110;功能指令为 11010001;会话密钥为 00110101;飞机公钥为 00000101;私钥为 01001101时,通过对吊舱的仿真,在 CCS中使用探针、FileI/O和图形显示功能将吊舱的发送序列显示,见图 5。
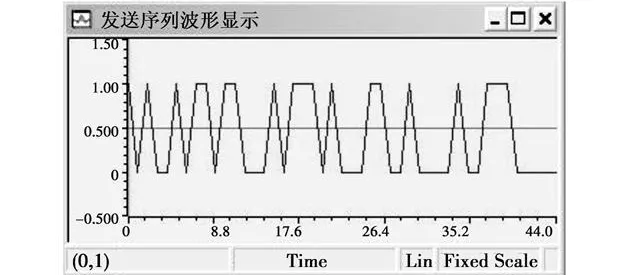
图 5 发送序列的图形显示Fig.5 Graphic display of sending message
从存储器和图形显示可以看出吊舱的整个发送序列,见表 2。

表 2 发送序列Table 2 Sending message
然后通过对导弹的仿真对发送序列进行解密认证。在不对指令信息作任何更改的情况下,从存储器可以看出导弹解密后得到的指令明文和认证数据如表3所示。

表 3 解密得到的明文序列Table 3 Original message after decryption
从表 3可以看出正常情况下导弹可以很好地解密出指令明文并对指令进行认证。本文还对以下几种情况进行了仿真实验:1)在发送途中更改发送序列;2)在计算认证码后更改明文序列;3)利用第三方的私钥进行签名。从仿真结果可以看出在这几种情况下导弹计算得到的新校验码与原校验码均不相同,因此导弹认为指令是不完整或不真实的。
以上序列一次加密所需时间约为 18.3μs,一次解密验证所需时间约为 2.5μs,其加解密时间都非常短,能够满足导弹的时效性要求。
5 结论
本文研究了一种含有载机认证的无线电控制指令加密方案。该方案中,传给导弹的信息中不仅包含有加密后的会话密钥和指令信息,还包括消息认证码,导弹会对接收到的信号进行认证,只有认证协议正确,导弹才能进一步对控制指令解码,这样确保导弹只接收发射导弹的载机的控制指令。同时采用非线性函数来产生加密序列,改变仅靠加大 LFSR长度的方法来增加密钥空间范围。仿真结果表明,本文提出的方法有效地提高了指令的安全性,在不影响导弹时效性的前提下,很好地解决了指令干扰问题。
[1] 吴文超,杜海文,韩统.空地电视制导导弹作战使用研究[J].电光与控制,2008,15(7):55-57.
[2] 李望西,黄长强,庞春雨.基于神经网络的电视遥控制导导弹损失率预测[J].电光与控制,2009,16(6):89-92.
[3] МОДЕЛЬ ПРОЦЕССА ПРОСТРАНСТВЕ ННОГО НАВЕДЕ НИЯАУРС ТКСН В УСЛ-ОВИЯХ ОЭ И РЭН[R].2000.
[4] 付裕松.H-XX电视制导训练弹交联控制系统研究[D].西安:空军工程大学,2005.
[5] 李顺东,王道顺.现代密码学:理论、方法与研究前沿[M].北京:科学出版社,2009.
[6] 李骞,冯金富,潘勃,等.电视制导导弹无线电制导指令编码加密[J].电光与控制,2009,16(10):55-57.
[7] ARIK S.An neural networks and their paplieations[C]//Proceedings of the 7th IEEE International Workshop,2002(7):22-24.
[8] COA J.A set of stability criteria of delayed cellular neural networks[J].IEEE Trans Circuits Syst,2001,48(4):449-498.
[9] LI Zan,CHANG Yilin,JIN Lijun,et al.Analysis of FHMA performanceon block cipher based frequency-hopping sequences[C]//Communications Letters,IEEE,2004:434-436.
[10] HORAN D M,GUNEE R.A novel pseudorandom binary sequence generator for keystream generation[C]//Proceedings of the 2006 IEEE International Symposium on Circuits and Systems,ISCAS 2006:1358-1362.
[11] KAHATE A.Cryptography and network security[M].北京:清华大学出版社,2009.
[12] 罗焯炬.一个 DSP下实现快速 RSA加密的新方法[J].微计算机信息,2008,24(21):45-46.
[13] 姜阳,周锡青.DSP原理与应用实验[M].西安:西安电子科技大学出版社,2008.
