基于遗传算法的支持向量机短期风速预测
2010-08-29周同旭
周同旭
(皖西学院机械与电子工程学院,安徽六安 237012)
基于遗传算法的支持向量机短期风速预测
周同旭
(皖西学院机械与电子工程学院,安徽六安 237012)
对风电场风速实现较准确的预测,可以有效减轻并网后风电场对电网的影响。支持向量机模型的预测精度在很大程度上依赖于模型参数的选择,为提高预测模型的泛化能力和预测精度,应用遗传算法选择支持向量机的模型参数,再根据选择的参数对小时风速进行预测。实验结果表明本文方法能够获得较高的风速预测精度。
预测精度;支持向量机;遗传算法;小时风速
1 引言
随着我国能源结构的调整,可再生能源特别是风能的开发利用已得到高度重视,从技术成熟性和经济可行性看,风电在可再生能源中具有很好的前景[1]。随着风能的加速发展,越来越多的大型风电场纳入统调电网,风电在电网的比重越来越大,同时风电的强随机性增大了电力调度的难度。风速的准确预测有利于调度部门及时调整计划,从而减轻风电对电网的影响[2]。
目前,风速预测常用的方法包括两大类:传统方法和现代方法。前者包括线性外推法、回归分析法和时间序列法等。后者主要包括专家系统、支持向量机(SVM)[3]和人工神经网络(ANN)[4-5]等。人工神经网络一度成为预测领域的研究热点,然而,人工神经网络也有许多至今无法解决的问题。支持向量机是一种基于结构风险最小化原理的预测模型,其泛化能力要远好于神经网络和自回归模型,近年来也被一些学者应用于风速预测。支持向量机模型参数对预测精度有很大影响[6],然而参数的确定还缺乏严格的数学方法。杜颖等人提出了用网格搜索法对SVM参数进行优化选择[7]。郭辉等人提出基于三步搜索法的支持向量机参数优化方法[8]。这些方法都为支持向量机模型参数的优化选择提供了有效的途径。
遗传算法(GA)能使种群达到全局最优收敛。与传统算法相比,遗传算法无需先验知识,而且对初始参数不敏感,所以不会陷入局部极小点。本文利用遗传算法对支持向量机模型参数进行优化选择(GA-SVM),并用参数优化后的支持向量机模型对某风电场的小时平均风速进行预测,取得了较高的预测精度。
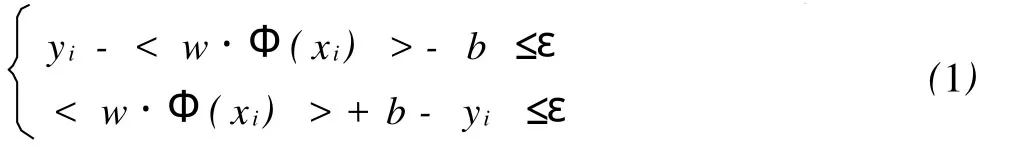
2 支持向量机
支持向量机应用于回归方面,主要有Vapnik提出的ε-回归支持向量机(ε-SVR)。设有回归函数f(x)=
式中,i=1,2,…,k。
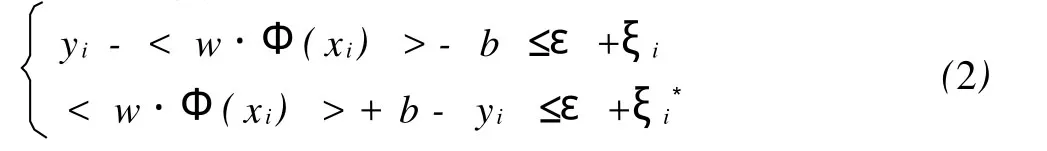
优化目标为:

约束条件为
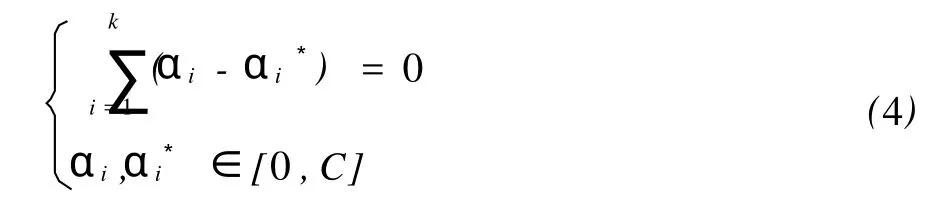
求解上述问题并引进核函数 K(x,x′)后,得到w和待估计函数
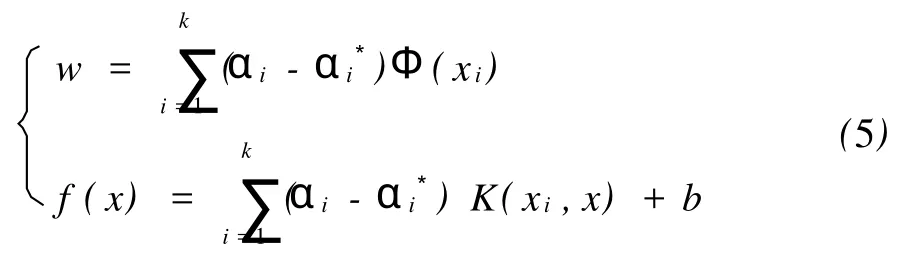
其中(αi-α*i)≠0对应的 xi即为支持向量。
在SVM模型中通过对上述三种核函数的比较,发现径向基核函数性能最好,本文也将采用径向基核函数。其表达式为:
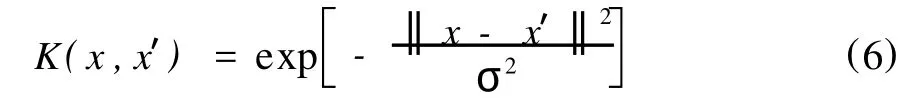
3 遗传算法
支持向量机模型参数ε、C和核函数参数σ2的选择对精度影响很大,目前还缺乏严格的数学计算方法,这三个参数的组合本质上是一种优化过程。本文将遗传算法应用于参数ε、C和核函数参数σ2的优化中,适应度函数采用均方根误差的倒数。

其中,N为样本个数,WR为实测值,WF为预测值。算法步骤如下:
Step1编码:将解空间的数据ε、C和σ2表示成遗传空间的基因型数据,这些基因型数据的不同组合就构成了不同的点。本文采用二进制编码法。
Step2初始化种群:随机产生 N个初始基因型数据,每个基因型数据称为一个个体,N个个体构成一个群体。GA以这个N字符串为初始点开始迭代。
Step3个体适应度计算:计算个体适应度,并判断是否符合优化准则,若符合,输出最佳个体及其代表的最优解,并结束计算,否则转向Step4。
Step4选择:根据每个个体的适应度值,选择一些优良的个体遗传到下一代群体中。适应性强的个体被选中的概率高,适应度低的个体可能被淘汰。
Step5交叉:将群体内的各个个体随机搭配成对,对每一个体以某个概率(称为交叉概率)交换它们之间的部分染色体。
Step6变异:对群体中的每一个个体,以变异概率改变某一个或某一些基因座上的基因值为其他的等位基因。
Step7判断运算:判断新一代群体是否满足结束条件,如果满足,则停止;不满足,则转至Step3步骤继续进行计算。
4 风速时间序列GA-SVM预测
仿真试验数据来源为我国某风电场2004年6月1日至6月15日共360小时平均风速数据,实验在CPU主频为2.4GHz、内存为2.0GB的PC机上进行,仿真软件为MATLAB7.4。
4.1 样本构造
风速数据是一组随时间变化的数据序列,记为{xt,t=1,2,…,n},支持向量机在选择输入输出变量前需对数据序列进行相空间重构,即把时间序列组转化为矩阵形式来寻找数据间的关系。将原数据序列进行相空间重构,构造样本对(Xt,Yt),其中 Xt= {xt-m,xt-m+1,…,xt-1},Yt=xt,m为输入向量的维数,xi为第i个样本。m的确定一般采用以均方根误差最小化为原则的增长法,即令 m从1开始逐渐增加,比较每次的验证误差,取误差最小时的m值作为输入维数。通过计算风速时间序列自相关系数可以确定输入维数。本算例风速序列的自相关系数曲线如图1所示。
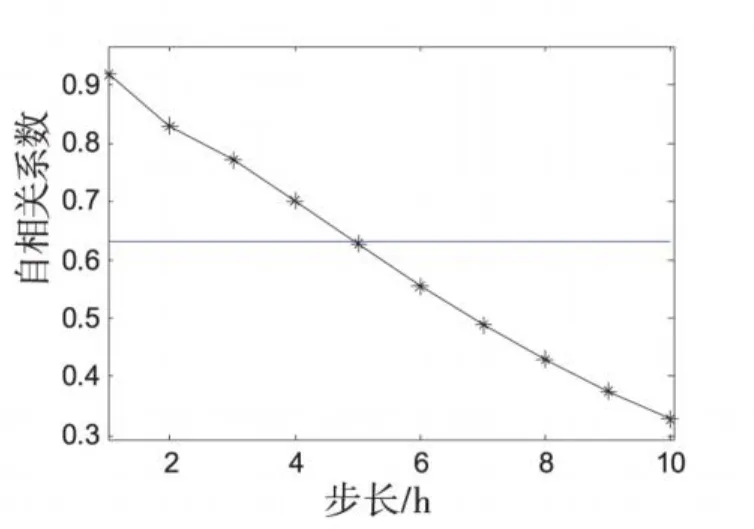
图1 风速序列自相关系数
取当自相关系数降至1-e-1时的延时步长5做为输入样本的维数m,即用前5天的风速预测第6天的风速。按照输入样本的维数,从原始数据中构造200个训练样本对和50个测试样本对。
4.2 归一化处理
对支持向量机预测模型的输入变量采用如下规范化的方法进行预处理。设风速序列最大值为 vmax,最小值为vmin,某一个风速v的规范化变量定义为:

这样每个输入变量的取值范围都在0~1之间,皆是具有相同尺度的无量纲量。
4.3 参数寻优
利用上述遗传算法的步骤对SVM的参数ε、C和σ2的最佳组合进行优化,采用二进制编码方法,设置种群规模为100,每个个体由代表三个参数的三个基因组成,每个基因长度均为40位,所以每个个体码串长度为120位,进化代数最大值设为200,交叉概率0.8,变异概率为0.1。最后得到参数最优化组合为:
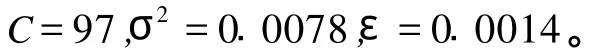
4.4 支持向量机建模
根据样本集建立如式(3)所示的目标函数,并用序列极小化训练算法求解,得到解 ai和a*i,i=1,2,…,k;将得到的拉格朗日乘子代入式(5)中,再利用预测样本对未来某一点风速进行预测。
4.5 SVM训练与预测
采用数据滚动方法对模型进行训练和预测,以进行后1h的风速预测。依此类推完成全部的风速预测,这样使网络能够反应风速最新变化规律。采用绝对百分比误差(APE)、平均绝对百分比误差(MAPE)对预测效果进行评价。
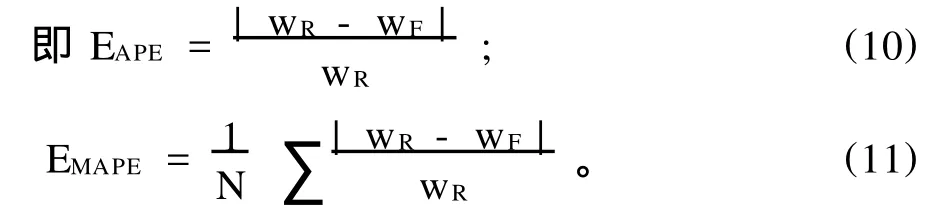
为了说明支持向量机在预测方面的性能以及遗传算法在SVM参数寻优方面的有效性,本文将GA-SVM法、文献[7]提出的SVM网格搜索参数法(GRID-SVM)以及BP神经网络法分别应用于风速预测。这里的BP神经网络层数确定为3层,学习和测试样本与SVM相同,输入层节点数为5,输出层节点数为1,隐含层节点通过实验比较取12个。神经网络第一层与第三层选用线性传递函数,第二层选用对数S型传递函数,利用L-M法进行训练。图2(a)、(b)、(C)分别是BP、GA-SVM和GRID-SVM三种方法的预测曲线。表1为三者预测结果。从图2的预测曲线和表1的数据可以看出:
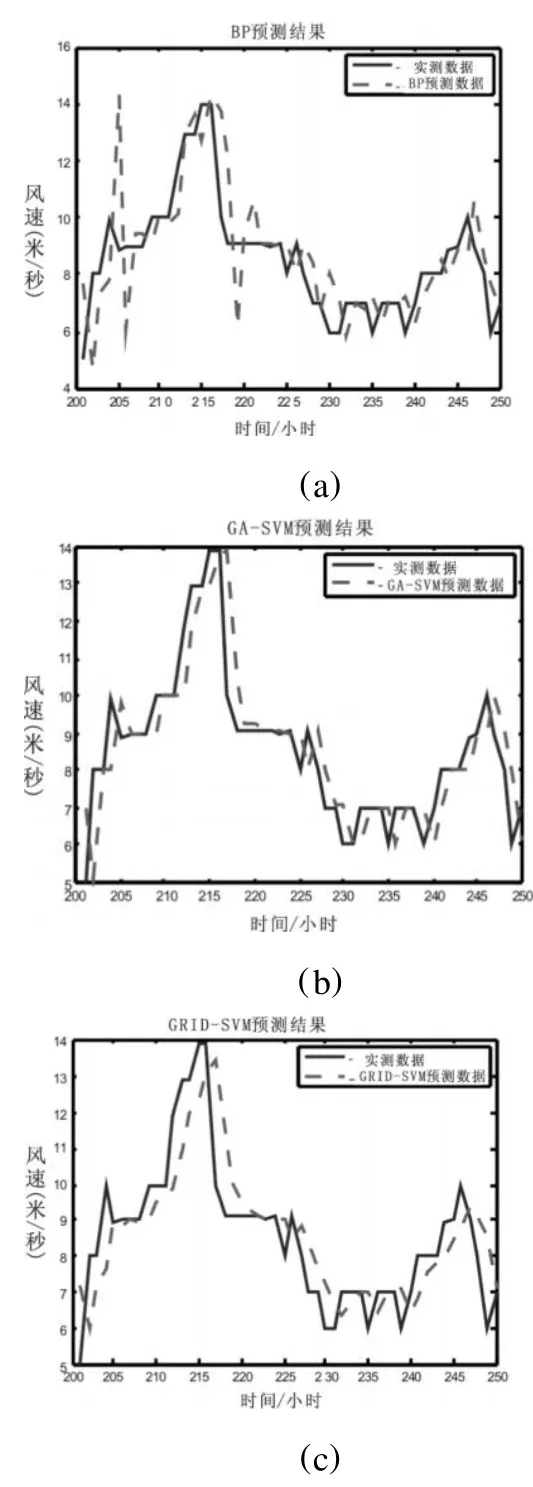
图2 预测曲线
(1)BP预测方法总体预测效果并不理想,其 MAPE达到15.2%。显然基于支持向量机的两种方法GA-SVM和GRID-SVM的预测效果均好于BP神经网络,这是因为SVM模型基于结构风险最小化原则,得到的是全局最优解,其泛化性能高于BP神经网络。
(2)在训练时间方面,虽然SVM方法训练和预测时间比BP要快得多,但参数寻优耗时较多,所以从表1看出,GA-SVM和GRID-SVM两种方法的总耗时均多于BP网络,GA-SVM较GRID-SVM耗时要少。
(3)通过试验发现,GA-SVM法比 GRIDSVM法具有更高的预测精度,两者的MAPE分别为9.7%和10.6%。
为进一步实验验证该算法,本文将 GA-SVM网络与RBF、BP网络同时对美国加州某风电场的两个测风站的风速进行预测。RBF网络采用从样本中选择固定隐层中心的方法,隐层神经元使用相同宽度,输出层权值使用最小二乘法求解。BP隐层函数选择高斯函数。GA-SVM采用前文使用的网络结构及算法。通过实验得到如表2所示的结果。
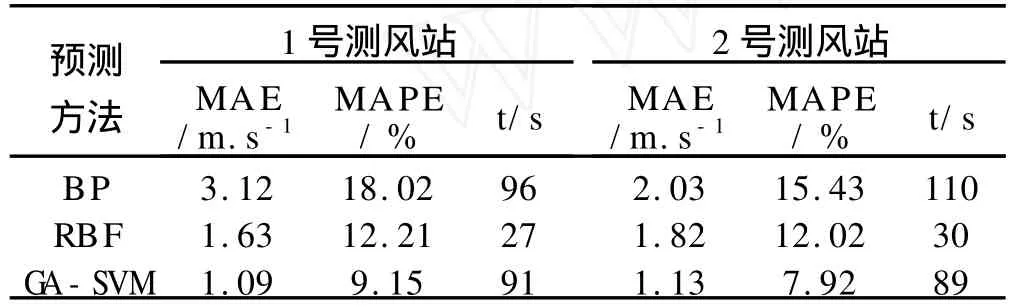
表2 三种方法预测结果
结果表明在这三种网络模型中,GA-SVM网络具有最好的学习、映射和泛化能力,其绝对百分比误差和平均绝对误差比BP、RBF网络都小。
5 结束语
本文提出了一种结合了遗传算法的支持向量机风速预测模型。支持向量机基于结构风险最小化,具有优越的泛化性能,得到的是全局最优解,解决了采用神经网络方法时无法避免的局部极值问题;通过遗传算法对支持向量机模型参数进行优化选择,保证了较高的预测精度。仿真表明 GA-SVM法相对于GRID-SVM和BP神经网络法具有更高的预测精度及更强的鲁棒性,预测风速的MAPE在10%以内,达到很好的效果。
[1]Alexiadis M,Dokopoulos P,Sahsamanoglou Het al.Short Term Forecasting of Wind Speed and Related Electrical Power[J].Solar Energy,1998,63(1):61-68.
[2]潘迪夫,刘辉,李燕飞.风电场风速短期多步预测改进算法[J].中国电机工程学报,2008,28(26):87-91
[3]王慧勤.基于支持向量机的短期风速预测研究[J].宝鸡文理学院学报(自然科学版),2009,29(1):16-18.
[4]Kariniotakis G,Stavrakakis G,Nogaret E.Wind Power Forecasting Using Advanced Neural Network Models[J].IEEE Trans.on Energy Conversion,1996,11(4):762-767.
[5]Li Shuhui,Wunsch D C,Giesselmann M G,et al.Using Neural Networks to Estimate Wind Turbine Power Generation[J]. IEEE Trans.on Energy Conversion,2001,16(3):276-282.
[6]Ping-Feng Pai,Wei-Chiang Hong,and Yu-Shen Lee1. Determining Parameters of Support Vector Machines by Genetic Algorithms-Applications to Reliability Prediction [J].International Journal of Operations Research,2005,2 (1):1-7.
[7]杜颖,卢继平,李青,等.基于最小二乘支持向量机的风电场短期风速预测[J].电网技术,2008,32(15):62-66.
[8]郭辉,刘贺平,王玲.最小二乘支持向量机参数选择方法及其应用研究[J].系统仿真学报,2006,18(7):2033-2051.
Forecasting of Short-term Wind Speed with Support Vector Machine Based on Genetic Algorithms
ZHOU Tong-xu
(College of Mechanical and Electrical Engineering,West Anhui University,L u’an237012,China)
Giving a high precise wind speed forecast for wind farms can effectively relieve disadvantageous impact of wind power plants on power systems.The selection of parameters for Support Vector Machine(SVM)has a large impact on the forecasting accuracy.For enhancing the generalization performance and prediction accuracy,genetic algorithms(GA)are applied to select parameters for SVM model in this study,and then hourly wind speed are forecasted according the selected parameters.The simulation results show that using the model proposed on the paper to predict wind speed can achieve a high accuracy.
forecasting accuracy;support vector machines;genetic algorithms;hourly wind speed
O441.1
A
1009-9735(2010)05-0106-04
2010-08-07
皖西学院自然科学应用研究项目(WXZY0704)。
周同旭(1975-),男,安徽六安人,讲师,硕士,研究方向:检测技术,电力电子技术。
