无刷双馈风力发电系统模糊自抗扰最大风能捕获控制*

陈亦哲， 杨俊华， 吴 捷

(1.广东工业大学自动化学院，广东广州 510006;2.华南理工大学电力学院，广东广州 510641)

0 引言

变速恒频风力发电是目前主流的风能发电方式［1］，无刷双馈电机兼有笼型、绕线型异步电机和电励磁同步电机的优点［2］，功率因数和运行速度可调节。基于无刷双馈电机构建变速恒频风力发电系统是风力发电研究的又一热门课题，解耦控制则是无刷双馈风力发电机控制中的难点［3］。

自抗扰控制器(Active-Disturbance Rejection Control，ADRC)是一种改进型非线性PID控制器，比传统PID控制器具有更强的适应性和鲁棒性［4］，同时克服了传统PID误差取法不合理、没有误差微分提取办法、组合方式不理想等缺点，已较为广泛地应用于工程实际中。但ADRC算法较为复杂，其参数相对PID来讲较多，而参数选择的合适与否将直接关系到ADRC对实际对象控制效果的优劣。目前，其参数的整定通常都采用试凑法，工作量大，整定过程繁杂［5］。

文献［6］将ADRC引入双馈异步发电机有功与无功功率的解耦控制，通过扩展状态观测器和非线性控制器的应用，将有功功率与无功功率的控制作为两个独立的子系统进行设计。文献［7］将自抗扰控制技术引入到变速恒频双馈型风力发电系统的最大风能捕获控制中，采用扩张状态观测器对电压方程中的耦合项和电网电压等扰动项进行观测并加以补偿，提高了系统的跟踪性能，在不同风速下都有比PID控制更小的超调量和更快的响应速度，对电网电压的波动有较强的抑制能力。文献［8］根据自抗扰控制原理，将风能转矩的不确定性与系统的摩擦不确定性统一视为系统的未知干扰，通过扩张状态观测器来估计，利用非线性反馈控制律进行补偿，使系统控制律仅与系统给定输入和输出有关，减少控制过程中的检测量，简化了控制过程。文献［9］在常规PID控制和模糊控制的基础上，提出了一种PID参数模糊自整定控制器，采用模糊推理对PID控制器的控制参数进行在线调整，给出了参数整定的基本原则。文献［10］提出了一种新的自适应模糊ADRC，引入模糊逻辑控制，运用模糊控制的适应能力来调整非线性反馈的参数。

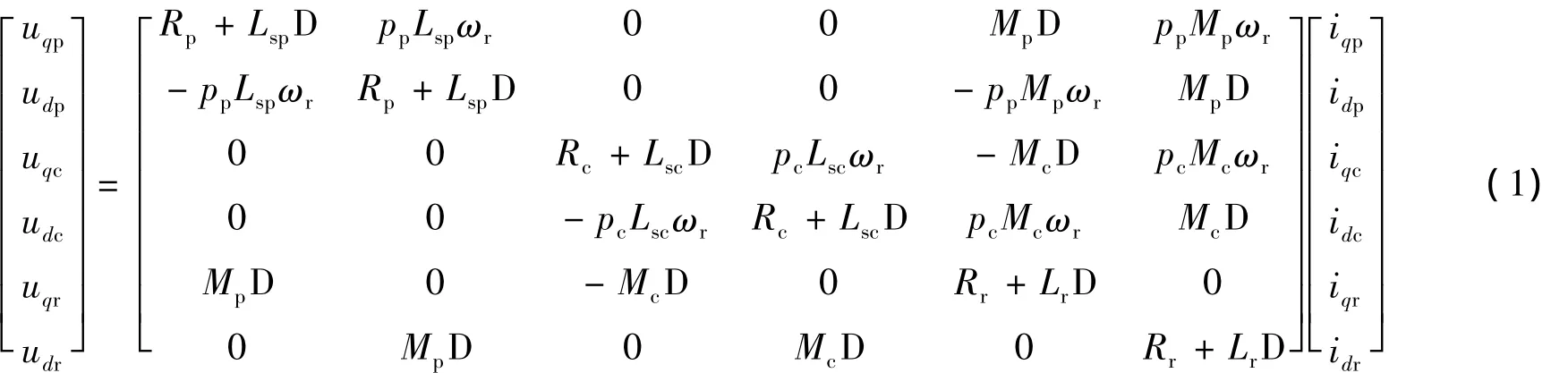
本文利用ADRC实现无刷双馈风力发电机有功功率与无功功率的解耦控制，结合最大风能捕获控制的要求，建立了风力发电机组的功率控制模型。通过在ADRC中引入模糊逻辑控制对ADRC非线性模块进行参数整定。

1 无刷双馈电机的数学模型及功率解耦

1.1 数学模型

无刷双馈电机转子坐标系下电压源d-q轴模型［11-12］如下:

式中:rp、Lsp、Mp——功率控制绕组的电阻、自感和功率绕组与转子的互感;

rc、Lsc、Mc——控制绕组的电阻、自感和控制绕组与转子间的互感;

rr、Lr、ωr——转子电阻、自感和电机的机械角速度;

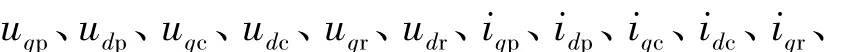
idr——电压、电流的瞬态值;

D——微分算子。

下标p——功率绕组;

下标c——控制绕组;

下标s——定子侧;下标r——转子侧;

下标q、d——d-q坐标系下q、d轴分量。

电磁转矩方程为

1.2 功率解耦

有功功率和无功功率的解耦控制是无刷双馈风力发电系统中的关键技术。

为方便控制，忽略定子绕组电阻、磁路饱和及转子饱和的影响，将无刷双馈电机(Brushless Doubly Fed Motor，BDFM)分为两个独立的子系统，功率绕组和控制绕组分别建立在各自的同步坐标系统下，得到BDFM的有功功率、无功功率和控制绕组电压方程［13］。通过适当的补偿抵消功率绕组和控制绕组之间的交叉耦合，抵消iqc、idc对Uqc、Udc的影响，进而达到通过调整Uqc、Udc来控制iqc、idc的目的。同样，绕组的有功功率P和无功功率Q也可通过控制iqc、idc来实现。控制思路为

1.3 BDFM风力发电机最大风能捕获控制

根据空气动力学的基本理论，一台实际的风力机所捕获的风能可转变为机械输出功率Pm的表达式为［14］

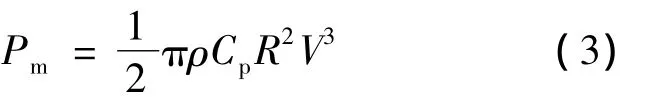
式中:ρ——空气密度;

R——风轮半径;

Cp——风力机的风能利用系数;

V——风速。

风能利用系数Cp不是一个常数，它随风速、风力机转速、风力机叶片参数(如桨距角β等)而变化，通常，Cp=Cp(β、λ)，λ 定义为叶尖速比:

式中:ω——风轮转速。

图1为不同桨距角时，风力机风能利用系数CP与叶尖速比λ的关系图。

图1 风力机CP与λ的关系

由图1可知，当桨距角β一定时，存在一个最优的叶尖速比λ，使风能利用系数CP达到最大值CPmax。维持风力机运行在最优的叶尖速比状态即可实现最大风能捕获控制。根据风力机功率特性曲线，得到在一定浆距角下的最佳叶尖速比λ［15］。opt

由式(4)得发电机转速参考值表达式为

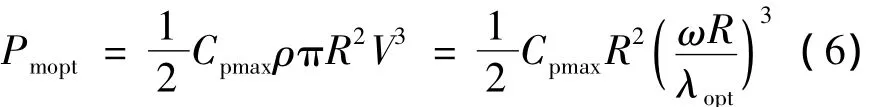
风力机输出功率与BDFM功率绕组有功功率的关系为

某一风速下最大功率曲线的表达式为

式中:ωn——发电机的自然同步转速;

ωr——发电机转速;

Pp——满足实现最大风能捕获的功率绕组有功功率。

根据式(3)～(7)，得到最大功率转速参考值ω*，进而求出Pp。即功率绕组有功功率的给定值P*=Pp。

BDFM中各绕组间无功功率的关系式为

风电系统转子运动方程为

式中:Tr——风力机转矩;

Te——发电机转矩;

J——系统转动惯量;

Kd——转动阻尼系数。

2 控制系统的设计

2.1ADRC原理

ADRC由非线性跟踪-微分器(TD)、扩张状态观测器(ESO)和非线性状态误差反馈控制律(NLSEF)组成(见图2)。TD用来实现对系统输入信号的快速无超调跟踪，并给出其“广义”微分信号;通过扩张状态观测器(ESO)对系统的状态z1，…zn和总扰动分别进行估计;NLSEF利用TD和ESO的输出之差来生成控制量:

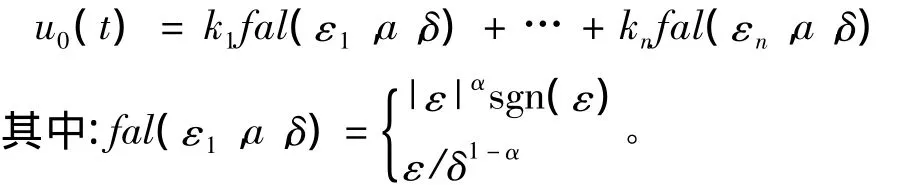
图2 ADRC结构框图

NLSEF利用状态误差反馈的非线性组合和总的扰动，估计zn+1，构成系统的控制量:

由文献［11］中的BDFM同步坐标系下有功功率、控制绕组电压可知，对有功功率的控制就是对的控制，iqc，ce的动态过程为

把非线性及耦合项f(iqc，ce，idc，ce)作为系统的扰动项，根据ADRC的原理及控制框图2，结合交流励磁变速恒频风力发电技术，设计有功功率的ADRC。

2.2 控制器的设计

(1)TD的设计:

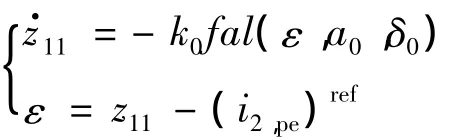
(2)扩张状态观测器(ESO)为

(3)非线性反馈控制律(NLSEF)为

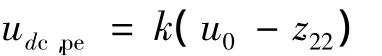
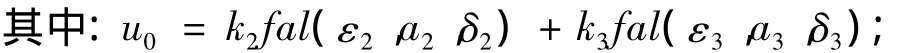
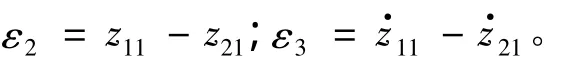
式中:α0、α1、α2、δ0、δ1、δ2、δ3、k0、k21、k22、k2、k3为待定参数，都需经调整确定。从控制律的结构表达式可见，系统控制律与系统内部的参数无关，而只与系统的输出和给定输入有关。

2.3 自抗扰控制的参数整定

由于ADRC三个部分相互独立，其参数可按“分离性原理”进行独立整定。在ADRC参数整定的过程中发现，TD的参数可以固定化、ESO的参数可由两个参数的关系确定。非线性控制律NLSEF的作用是生成一个控制量，相当于PD控制器控制一个“积分串联型”的对象，可以用非线性反馈控制律参数k2表示比例增益，k3表示微分增益。在实际运用中，对NLSEF参数的整定可利用PD控制器中的P、D的模糊整定方法［9］。因此，运用模糊控制原理，在常规模糊控制器的基础上，以误差e和误差变化率ec作为输入，利用模糊控制规则在线对k2、k3参数进行修改，进而满足不同时刻的e和ec对k2、k3自整定的要求。

针对k2、k3分别建立如表1、2所示的参数整定模糊控制表。

将系统误差E和误差变化率EC变化范围定义为模糊集上的论域:

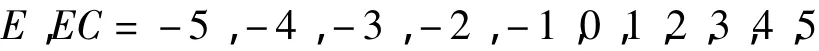
表1 k2的参数模糊整定表

表2 k3的参数模糊整定表

设计模糊控制子集为

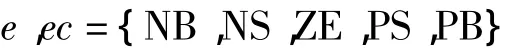
考虑到对论域的覆盖程度、灵敏性、稳定性及鲁棒性，设计e，ec和k2、k3各模糊子集的隶属度函数均选用正态分布函数，根据各模糊子集的隶属度赋值表和各参数模糊控制模型，应用模糊合成推理设计出k2、k3的模糊矩阵表，查出修正参数代入计算式:

即得出整定后的k2、k3，结合ADRC参数整定原则和ADRC公式，即可得到合理的ADRC。

3 仿真结果及其分析

运用MATLAB/Simulink进行仿真，系统框图如图3所示。

无刷双馈发电机参数如下:互感Mp=69.31 mH，自感Lsp=71.38 mH，电阻rp=0.435 Ω，互感Mc=60.21 mH，自感Lsc=65.33 mH，电阻rc=0.436 Ω，转动惯量J=0.3 kgm，转子的电感Lr=142.8 mH，电阻rr=1.63 Ω，功率绕组的极对数pp=3，控制绕组的极对数pc=1，风轮半径R=4 m。

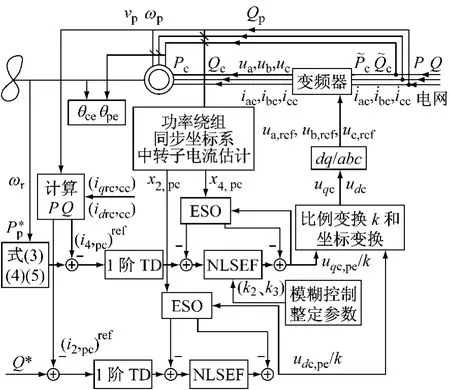
图3 BDFM风力发电机组功率控制系统框图

图4显示给定转速为ω=25 s，在t=0.1 s时起动，以达到稳态值95%为参考，ADRC的上升时间为0.9 s，PI控制的上升时间为4.5 s;当到达6 s时，ADRC的稳态误差为0.001，而PI的稳态误差为0.450。

图4 ADRC与PI仿真结果比较

选取与风速25 r/s时相同的参数，针对不同风速给定进行仿真试验。图5表示10～30 s内风速为7 m/s，30～60 s内风速由7 m/s阶跃到9 m/s，而60 s后风速又变到7 m/s。无功功率(见图6)10～20 s给定为 -10 kVar，20～40 s阶跃到 -5 000 kVar，在40～80 s时变回 -10 kVar。

图5 风速

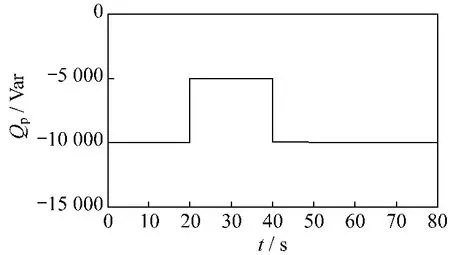
图6 无功功率给定

图7表示当风速分别为7 m/s和9 m/s时发电机发出的有功功率的变化。此时发电机处于亚同步状态，需要通过控制绕组从电网吸收能量。

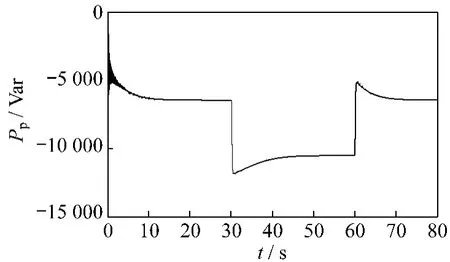
图7 功率绕组有功功率

图8为功率绕组无功功率的仿真结果，由图可知，系统能够跟踪给定值变化，表明风速的变化与无功功率的调整互不影响，实现了风力发电系统的功率解耦控制。

图8 功率绕组无功功率

图9表示风力机实际功率系数曲线特性，功率系数都维持在最大值(0.441)，基于最佳负载曲线的控制方法实现了最大风能的捕获。

图9 风力机功率系数

4 结语

将ADRC理论应用到无刷双馈变速恒频风力发电系统转速及功率控制中，在MATLAB/Simulink上建立了整个变速恒频风力发电功率控制系统的模型。仿真结果表明:采用ADRC能够有效减小耦合项及电网电压波动的影响，在电网波动的情况下，能够有效跟踪最佳功率点，实现最大风能捕获，验证了基于自抗扰理论的功率解耦控制策略的有效性。

［1］王孝洪，杨金明，吴捷.变速恒频风力发电系统中的电力电子技术［J］.电机与控制应用，2009，36(11):12-17.

［2］杨俊华.无刷双馈风力发电系统及其控制研究［D］.广州:华南理工大学，2006.

［3］黄守道，王耀南，王毅，等.无刷双馈电机有功和无功功率控制研究［J］.中国电机工程学报，2005，25(4):87-93.

［4］韩京清.自抗扰控制器及其应用［J］.控制与决策，1998，13(1):19-23.

［5］于希宁，朱丽玲.自抗扰控制器的动态参数整定及其应用［J］.华北电力大学学报，2005，32(6):9-13.

［6］张先勇，吴捷，杨金明.基于自抗扰解耦的变速恒频风力发电功率控制系统［J］.电气传动，2007(2):9-12.

［7］王晓兰，梁波，郑伟.有效抑制电网波动影响的最大风能捕获控制［J］.电机与控制应用，2009，36(3):14-17.

［8］杨金明，吴捷，杨俊华.基于自抗扰控制器的风力发电系统的最大风能捕获控制［J］.太阳能学报，2004，25(4):525-529.

［9］陈洪，高延滨，孙华.自适应模糊自抗扰控制器的研究与设计［J］.微计算机信息(测控自动化)，2008，24(8):32-33.

［10］张春，江明，陈其工.PID参数模糊自整定控制器的设计与研究［J］.机电工程，2006，23(9):19-21.

［11］Zhou D，Spee R，Gerald C.Alexander experimental evaluation of a rotor flux oriented control algorithm for brushless doubly-fed machines［J］.IEEE Trans Power Electronics，1997，12(1):72-78.

［12］Zhou D，Spee R.Synchronous frame model and decoupled control development for doubly-fed machines［C］∥25thAnnual IEEE Power Electronics Specialists Conf，Taipei，China，1994(2):1229-1236.

［13］王琦，陈小虎，纪延超，等.同步坐标下的无刷双馈风力发电机控制系统［J］.南京理工大学学报，2006，30(6):673-678.

［14］Manwell J F，McGowan J G，Rogers A L.Wind energy explained:theory，design and application［M］.England:John Wiley＆ Sons，Ltd，2003.

［15］刘其辉，贺益康，赵仁德.变速恒频风力发电系统最大风能追踪控制［J］.电力系统自动化，2003，27(20):62-67.