双馈风力发电系统中发电机等效电感的选取
2010-08-28李进泽
李进泽
(中国南车株洲电机有限公司,湖南株洲 412001)
0 引言
在目前的风力发电机技术中,大功率并网型风力发电机是其主流。作为并网型风力发电机之一的双馈风力发电机(以下简称发电机),具有所需变流器容量小、变速范围宽、输出电能质量高且功率因数可调等特点[1],但输出电能质量的高低主要受发电机及变频器的影响,其中最大的谐波源是转子回路上的变频器[2]。如果发电机能与变频器很好的匹配,将可从根源上减小系统的谐波和纹波。本文从双馈风力发电系统主电路的工作原理[3]出发,推导出变频器对发电机等效电感值的要求,并通过仿真验证了其正确性。
1 主电路工作原理
通过文献[4]对发电机电磁关系的分析可知,发电机可用图1所示的等效电路图表示。

图1 发电机等效电路图
由图1(a)可知,发电机就是一绕线式异步电机,只是在其转子上外加变频电源进行转速与功率的调节。图1(b)考虑到变频器加在发电机的转子侧,为简化后续计算,将整个发电机简化为一电感与电阻串联并折算到转子侧,同时将发电机所接的网压也折算到转子侧,且以下所有的分析均基于转子侧进行计算。
由图1所示的发电机等效电路图可得到整个双馈风力发电系统的主电路,如图2所示。

图2 双馈风力发电系统主电路图
其主电路的微分方程如下:
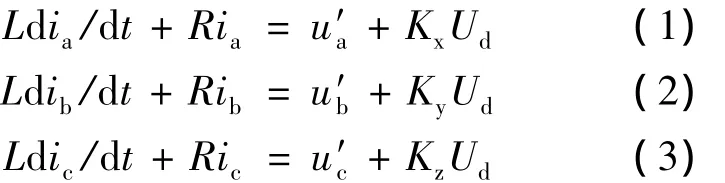
式中:Ud——变频器直流母线电压;
L——发电机等效电感;
R——发电机等效电阻;
u′a、u′b、u′c——发电机定子各相网压折算值;
Kx、Ky、Kz——开关系数[5]。
2 电感值计算原理
考虑到整个双馈风力发电系统是一对称三相系统,故只需讨论其中任意一相即可,其他两相可用同样的方法得到相同的结果。以下分析以A相为例。
由文献[3]在得出发电机所需要的转子电流后,可以通过滞环比较法[5]来控制主电路中绝缘栅双极晶体管(IGBT)的通断,使发电机三相转子电流的波形接近所需波形。
图3为变频器的实际输出电流if跟踪指令电流ir的夸张画法,H为电流纹波的大小。从图3可看出,要让实际电流的纹波限制在H内,则需让if在每个指令周期内的斜率比ir的斜率要大。对于双馈风力发电系统,ir是一确定的正弦波。因此,在计算发电机的等效电感L时,可通过跟踪一正弦波电流推导出来。
图4为夸张画法的一段正弦指令电流波形,即ir=Irmsin(ωrt)。图中T为变频器的开关周期,t0为任选的一个工作时间起点,θ为t0处曲线斜率,yt0+T为t0处切线在t0+T处的幅值。

图3 实际电流跟踪指令电流

图4 夸张画法正弦波
由于变频器的开关频率很高,开关周期T很小,在t0到t0+T时间内,正弦波曲线可近似视为直线,故:
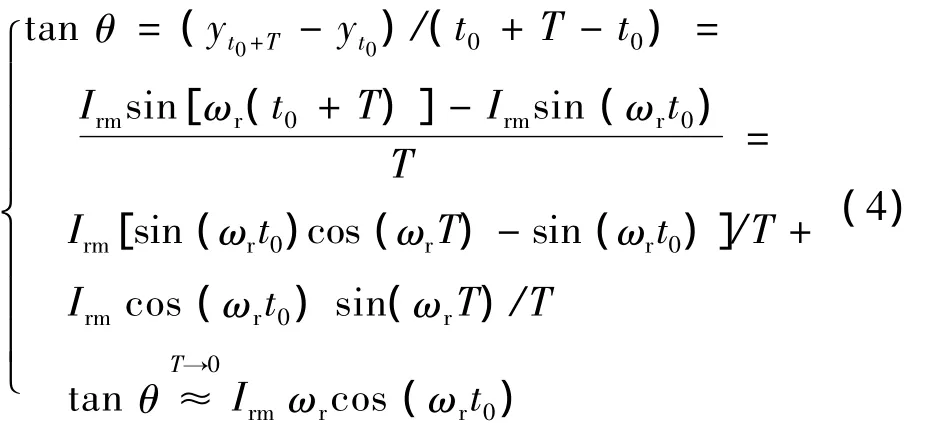
可得出:
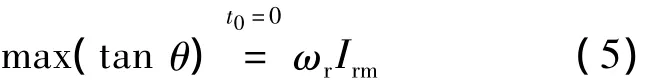
式中:Irm——ir的幅值;
ωr——ir的角频率。
变频器实际输出电流if由电网电压折算到转子侧的电压值与主电路中直流侧电压合成后在电感上产生。
由主电路的微分方程式(1)可得出:

式中:C——待定常数。
从式(5)有:正弦波的最大斜率处为if=0点。因此仅需求出ir0处的C值,为求得C值,由图3有在ir=0处的初始值为

由文献[5]可得Kx=4/9,结合式(6)和式(8),且由于变频器的开关频率都在几kHz到几十kHz,其开关周期T很短,趋近于0,考虑到HR<<,因此在i=0处有:r
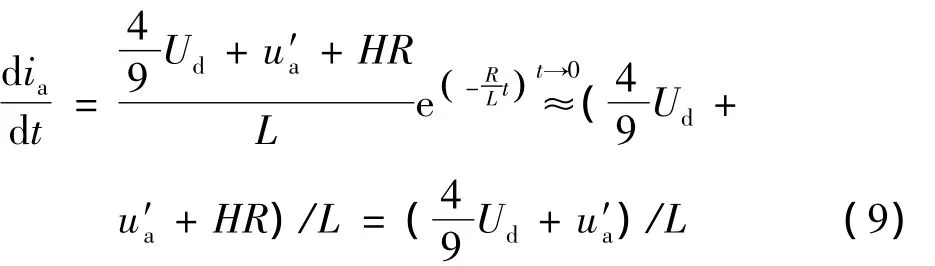
因需if的斜率大于ir的斜率,即 dif/dt>max(tan θ),所以求此时的极限工况,取电流ir与网压ua同相,即在ir=0处有u′a=0,结合式(5)和式(9)有:
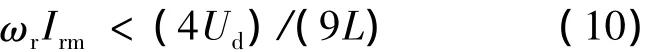
所以:

此为最大电感值,而最小电感值由主电路开关元件的最大开关频率限制。
由图3可知,在一个脉宽调制(Pulse Width Modulation,PWM)开关周期中,if与ir之差限制在H中,所以:
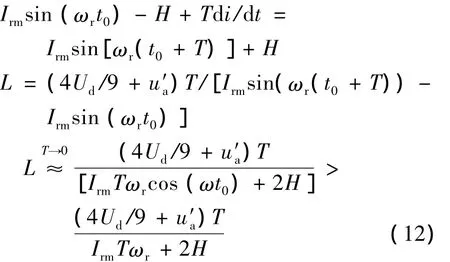
由于u′a为一正弦波,其最大值为网压折算到转子侧的折算值U′max,综合式(11)、(12)有:
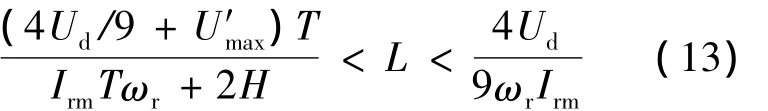
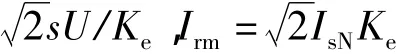

在实际电路中,由于发电机设计时尺寸及其他原因的限制,可能会造成发电机等效电感值偏小,此时可在变频器中串联一小电感使系统的电感值在式(14)范围内。
3 仿真研究
为验证上述计算结果的正确性,对国内某双馈风力发电系统进行了计算验证,并利用MATLAB环境下的Simulink工具箱构建了仿真模型。
该双馈风力发电系统的电网频率为50 Hz,发电机同步转速n0=1 500 r/min,定子相电压U=690 V,定子额定相电流IsN=666 A,额定转速nN=1 800 r/min,发电机的电压变比系数Ke=0.522,变频器中间直流电压Ud=1 150 V,输出电流的纹波控制在其最大值的5%以内,变频器开关频率为3 000 Hz,将以上数值代入式(14)可得:
0.000 77 H<L1+L′2<0.004 5 H (15)实际发电机的等效电路中定子电感值L1=0.000 17 H,转子电感折算到定子值为L′2=0.000 24 H,两者之和明显小于0.000 77 H,因此在转子侧串联了-0.000 2 H电感,折算到定子侧电感值为L′=0.000 734 H,其总电感值L1+L′2+L′=0.001 1 H,正处在式(15)所要求的范围中。
图5~7为仿真波形,图7中的1、0值为驱动电路送到开关元件的高低电平。从图中可看出,实际输出if波形的波动在(940sin 628t±47)A范围内,且fc<3 kHz,证实了电路中L选取合理。
4 结语
双馈风力发电系统中发电机等效电感L的选取对发电机与变频器是否匹配起决定性作用,它直接影响整个系统的电能质量及主电路开关元件的使用寿命。本文从变频器的实际电流跟踪理论电流的原理出发,推导出L的取值范围。从仿真及试验结果可看出,用本方法得出的L可满足动态跟踪性能,使系统的输出电流达到所规定的要求,并能使电路开关元件的fc在规定的范围内。
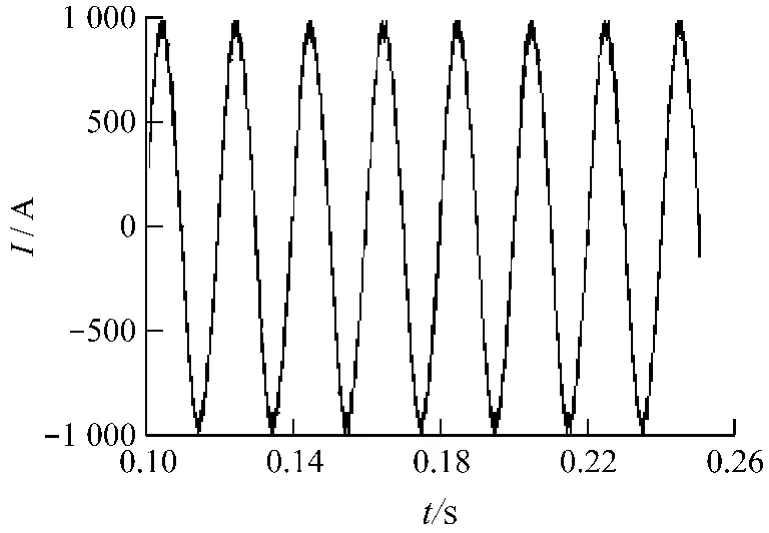
图5 实际电流输出波形
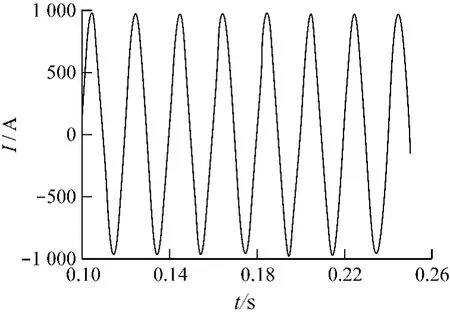
图6 指令电流波形
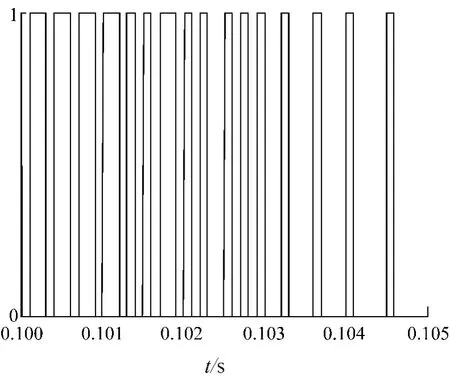
图7 一组开关元件驱动电平
[1]姚兴佳.风力发电机的研究现状[J].太阳能,2006(1):47-51.
[2]刘晓林.双馈型风力发电机的谐波抑制[J].电工技术,2009(12):50-56.
[3]胡崇岳.现代交流调速技术[M].北京:机械工业出版社,2001.
[4]吴冰,王建良.双馈风力发电机运行原理分析[J].电气开关,2008(6):6-7.
[5]王兆安,杨君,刘进军.谐波抑制和无功功率补偿[M].北京:机械工业出版社,1998.
