让数学插上想象的翅膀

由丽敏

（朝阳市建平县蒙古族学校，辽宁 建平 122400）

在数学教学的过程中，教师巧设一些比喻，能收到良好的教学效果。教师只要比喻设得巧，设得好，就能使本来晦涩难懂的概念、定义、公理、公式变得浅显明了，有的知识甚至能终生不忘，所以巧妙的比喻能成为学生学习的拐杖。笔者在近几年数学教学过程中，在这方面作了些粗浅的尝试。现整理如下，让大家指正。

“无理数是无限小数”好比“××学生是××学校的学生”

根据无理数的定义学生都知道无理数是无限不循环小数，可无理数是无限小数有的学生认为是错的，实际上无限小数包括无限不循环小数和无限循环小数，所以无理数是无限小数是对的。为了让学生便于理解，在教学中可举例：

小明是建平蒙古族学校八年三班的学生（√）小明是建平蒙古族学校的学生。（√）

无理数是无限不循环小数。（√）无理数是无限小数。（√）

学生很容易理解这是对的。建平蒙古族学校是大范围，它包括建平蒙古族学校八年三班。无限小数是大范围，它包括无限不循环小数。经过这样的举例，学生理解得很透彻并且记得很牢。

“对生活中的几何体进行分类”就好比对我们班的学生进行分类

数学学习中常常要进行分类：如在七年级上册第一章第一节《对生活中的几何体进行分类》的教学中，为了让学生更好的理解“分类时要有分类标准，分类标准不同分类也不同。”我们对我们班的学生进行分类，先按高矮分，看自己分在在哪一类；再按胖瘦分，看自己分在在哪一类；然后按男女分，看自己分在在哪一类；让学生亲身体验分类标准不同分类也不同。作了这样的比喻之后，学生在进行分类时先考虑分类标准然后进行分类，想出了好几种方法。

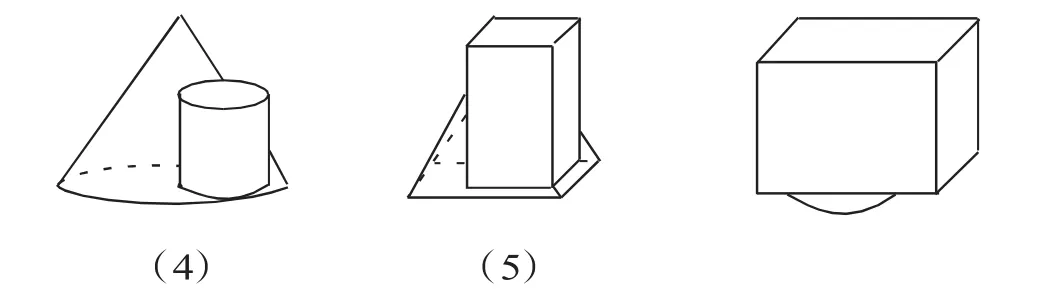
方法一：可以按柱、锥、球分

柱体有：圆柱、长方体、正方体

锥体有：圆锥、棱锥

球体有：球

方法二：还可以按组成面的平曲分

各个面都是平面的有：长方体、正方体、棱锥至少有一个面是曲面的是：圆柱、圆锥、球

方法三：按有无顶点分

有顶点的：长方体、正方体、棱锥、圆锥

无顶点的：圆柱、球

在教室内建立不同的平面直角坐标系，让学生更好地理解“平面直角坐标系建立的不同，平面内各个点的坐标也不同。”

建立适当的平面直角坐标系一节，为了让学生更好地理解“平面直角坐标系建立的不同，平面内各个点的坐标也不同。”我在教学时让学生在教室内建立不同的平面直角坐标系，分别让学生找到自己的坐标，体验坐标系建立的不同，平面内各个点的坐标也不同。

方程与函数是一对好朋友

一元一次方程与其对应的一次函数、二元一次方程与其对应的一次函数、二元一次方程组与其对应的两个一次函数都是一对好朋友。方程的问题可以用函数来解决，函数的问题也可以用方程来解决，好比“好朋友之间，你的事就是我的事，我的事就是你的事”。

A，B两地相距100千米，甲、乙两人骑自行车分别从A，B两地相向而行． 假设他们都保持匀速行驶，则他们各自到A地的距离s（千米）都是骑车时间t（时）的一次函数，1小时后乙距A地80千米；2小时后甲距A地30千米。

问：经过多长时间两人相遇？方法一：用方程解行程问题

解：设同时出发后t小时相遇，则

方法二：求出s与t之间的函数关系式，联立解方程组

对于乙，s是t的一次函数，可设s=kt+b.当t=0时，s=100；当t=1时，s=80.将它们分别代入s=kt+b中，可以求出k，b的值，也即可以求出乙s与t之间的函数表达式s=100-20t。

同样可求出甲s与t之间的函数表达式s=15t.

再联立这两个表达式，求解方程组就行了.

总之，对目前依然陌生的事物，教师要用熟悉的事物进行比喻，按照熟悉事物的性质、判定，加以类比研究，会有新的发展、新的创造，可减少学生学习随意性、盲目性，提高学习效率。