降落伞和尾翼相结合的末敏弹布局形式

高伟涛,崔占忠,李永远,郑 坚

(1.北京理工大学机电学院,北京 100081;2.二炮装备研究院,北京 100085)

0 引言

稳态扫描技术是末敏弹系统研制过程中的关键技术之一。目前,使子弹形成稳态扫描运动主要有两种技术方案:一是采用降落伞,二是采用气动力机构。由于本文所研究末敏弹的质量大,若采用降落伞布局形式,则所需的降落伞体积大,目标明显,系统易受到敌方的反击;若采用单翼或双翼布局,又受到阻力大小的限制。故在结构上采用了降落伞和尾翼相结合的布局形式。

1 末敏弹气动布局

末敏弹的气动布局主要根据其有无稳态扫描过程而分为两大类:一类为没有减速减旋装置的末敏弹,其主要代表有美国研制的GBU-97/B中的SKEET(斯基特)和X93式“大黄蜂”反坦克地雷、法国的ACDE等;而另一类则为有形成稳态扫描运动的减速减旋装置,其主要代表有美国的SADARM、德国的SMArt155和俄罗斯的RBK-500式SPBE反坦克子母炸弹。

目前,使子弹形成稳态扫描运动主要有两种技术方案[1]:一是采用降落伞,包括减速减旋降落伞和涡旋降落伞,通常称为有伞扫描,这种方式的优点是子弹下降和旋转的速度较慢,对敏感器件的反应速度要求不是很高,电子部件实现容易,缺点是降落伞体积大,易受敌方的反击,且系统受风的影响也较大;二是采用气动力机构,即采用双翼或单翼来形成所需的扫描运动,其缺点是翼片阻力面的大小受圆柱形子弹体横截面大小的限制,如果因战斗部的重量增大而需要增大阻力时,就会出现问题。

以上两类布局方式各有优缺点,针对二者的优缺点,本文提出了一种降落伞和尾翼相结合的布局形式。

2 伞翼结合的布局形式

2.1 伞翼布局原理

伞翼布局采用的是降落伞和尾翼相结合的布局形式,在子弹的尾部安装了三片弧形尾翼,在尾翼的上方悬挂有降落伞,其示意图如图1所示。

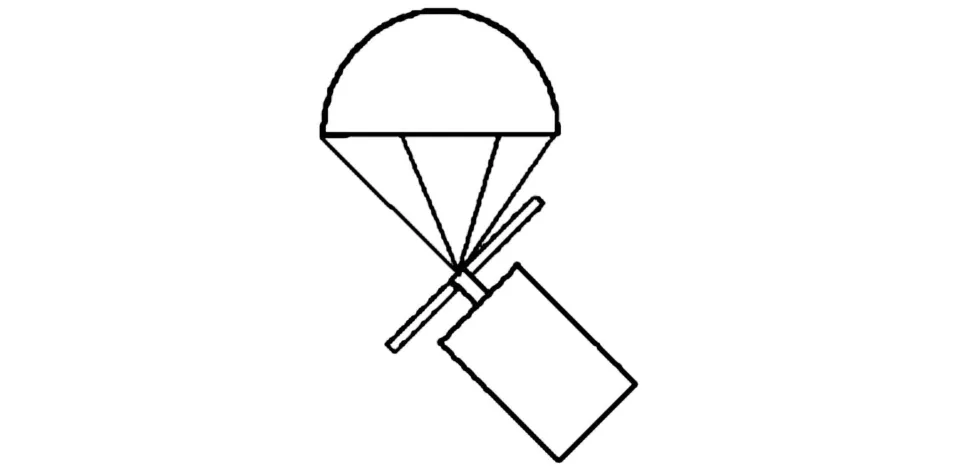
图1 伞翼布局示意图Fig.1 The sketch map of parachute-wing configuration

采用伞翼布局时,整个伞弹系统的气动参数由两部分组成,一部分为降落伞的气动参数,另一部分为子弹的气动参数。

2.2 伞翼布局的数学模型

为获得子弹气动参数,对翼展开后的末敏弹进行了数值风洞模拟。数值风洞模拟所建立基本守恒方程组为一般流体力学所具有的质量守恒方程(即连续方程)、动量守恒方程、能量守恒方程,并且在能量守恒方程中需要考虑热量传递。在这些守恒方程的基础上,加上必要的辅助方程就构成了控制方程。

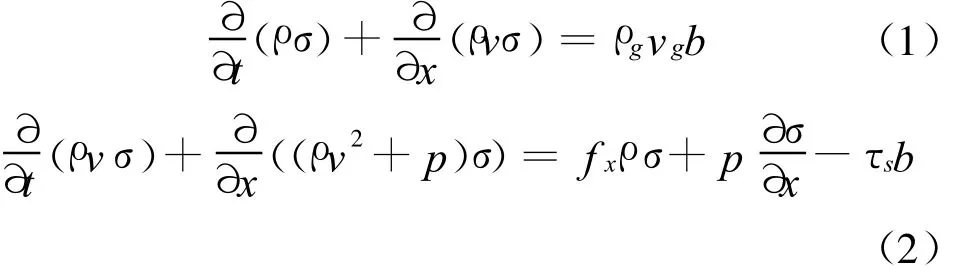
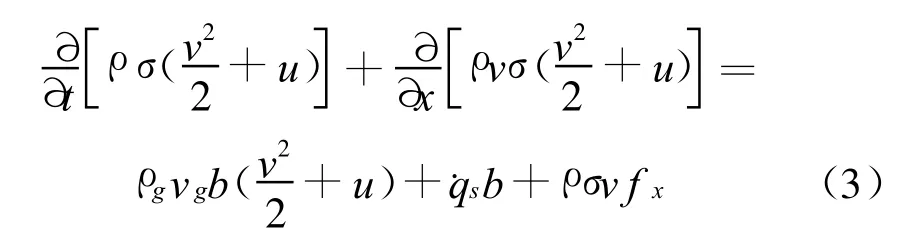
在对子弹进行气动仿真时,忽略了降落伞对子弹气动力计算的干扰。由于整个伞-弹系统降落的速度较小,远场的仿真域为圆柱体,轴向为20倍弹长,径向为10倍弹径,并对子弹网格进行了加密,建立的计算模型网格图如图2所示。

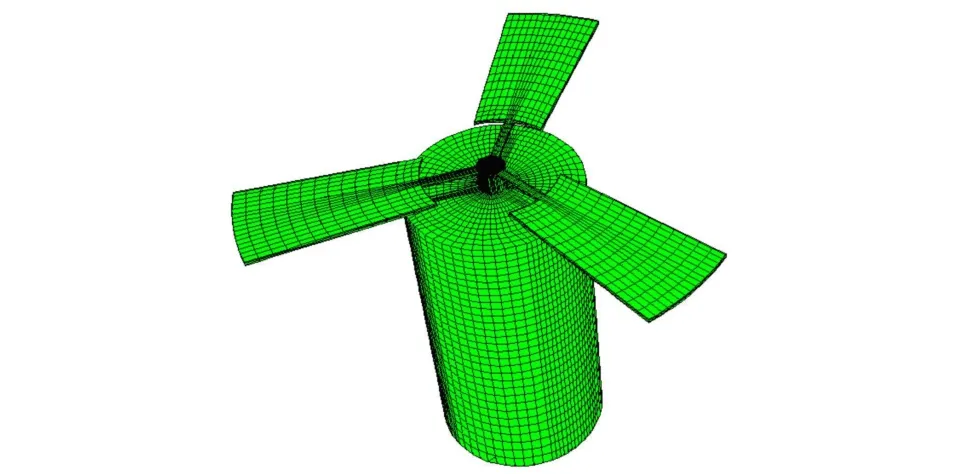
图2 计算网格模型Fig.2 Calculation mesh model

2.3 子弹气动仿真结果分析

根据计算流体动力学(CFD)理论,在Gambit和FLUENT软件平台上对计算模型进行了仿真,通过数值模拟方法研究子弹在自旋情况下的绕流流场特性以及子弹的气动参数计算。在末敏弹竖直下落时,尾翼的上部处于小负压区域,而子弹头部和三个尾翼下部压力相对别的部位来说比较大,最大为0.27个表压,因而受到的升力比较大,其他方向的力和力矩都比较小。子弹竖直下落即攻角为0°时的压力云图如图3所示。

图3 0°攻角子弹头和尾翼下部压力云图Fig.3 0°Attack angle the head of projectile and the lower-part of empennage＇s pressure nephogram

通过仿真计算可以得出,在马赫数为0.6时,由于尾翼的迎风面增大的缘故,随着攻角增大,阻力系数变化呈线性变化。在攻角增加到60°以后,阻力系数变化较缓,其变化趋势如图4所示。

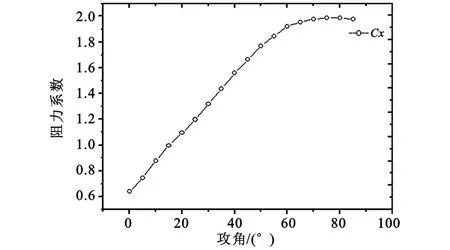
图4 阻力系数随攻角变化Fig.4 Resistance coefficient change with the attack angle

升力系数在攻角为28°时达到最大,约为2.2,其后升力系数开始减小,其变化趋势如图5所示。

图5 升力系数随攻角变化Fig.5 Lift coefficient change with the attack angle

本文气动仿真结果与试验结果吻合得很好。在攻角为30°,即扫描角为30°时,气动仿真计算的结果为1.319,试验的结果为1.301。气动仿真的结果为末敏弹的稳态扫描弹道仿真提供了可靠的参数。

3 双欧法六自由度方程组求解

在求解末敏弹飞行弹道时,为了克服子弹全方位六自由度解的奇异性问题,也就是三角函数在某些点趋于无穷值的问题,采用双欧拉法求解。子弹的姿态可以用3个欧拉角来确定,在航空领域广泛采用的是偏航角ψ、俯仰角ϑ和滚转角γ。求解欧拉角的欧拉方程具有奇异性,即:它有一对奇异点,使得在趋近奇异点的区域内产生解算误差,而在奇异点上无法解算[2-4]。

按照飞行力学的概念,地面坐标系变换到体轴系时,需要依次变换三次,如果变换顺序是按偏航、俯仰和滚转,则对应的偏航角、俯仰角和滚转角等为正欧拉角,分别记做 ϑ、ψ、γ,其角速度与子弹的转角速度 ωx1、ωy1、ωz1的关系如式(4)中所示,式(4)就是正欧拉方程组

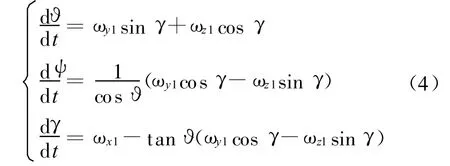
ϑ=±90°为此方程组的奇异点;而在ϑ=0°或ϑ=±180°附近时,方程解的精度将提高,在这里称此求解范围为正欧拉方程解的精华区;故在小俯仰角情况下,采用正欧拉方程求解可得到较理想的结果。但是对于某些俯仰角变化较大的系统,仅用正欧拉方程就难以求解了。

如果变换转动次序,按照俯仰、偏航和滚转,称此套欧拉角为“反欧拉角”,并用下标r表示。相应的欧拉运动学方程如式(5)中所示。

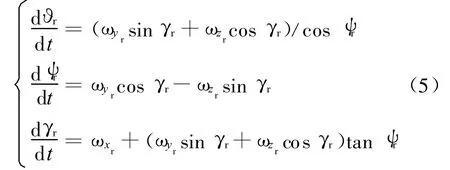
单就反欧拉方程来说,同样也存在着奇异性问题,即当ψr=±90°为此方程组的奇异点;而在ψr=0°或 ψr=±180°附近时,方程解的精度将提高,在这里称此求解范围为反欧拉方程解的精华区。

通过上面的分析可知正、反欧拉方程都存在奇异性的问题。但两者的精华区和奇异区却不尽相同,若能综合考虑,则可避免在正、反欧拉方程的奇异区内求解,从而达到克服欧拉方程奇异性的目的。

由式(5)可以看出,反欧拉方程精华区在ϑr=±90°附近,其奇异区在 ϑr=0°或 ϑr=±180°附近。这一点正好与正欧拉方程相反。如果以±45°或±135°为界将0°～360°的区域划分为如图 6所示的形式,利用正、反欧拉方程之间精华区和奇异区的倒挂关系,就可以避免求解过程中奇异性的出现,同时还可提高解的精度。

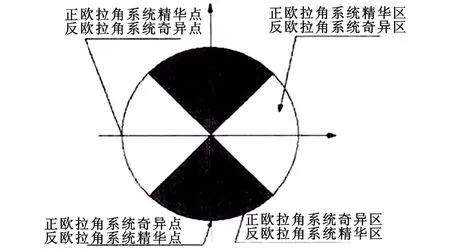
图6 正反欧拉方程精华区与奇异区Fig.6 The essence area and singular area of positive-negative euler equation

4 弹道仿真结果分析

把仿真所获得的气动参数代入伞弹系统的运动微分方程组中,运用双欧拉法求解该变系数的微分方程组。仿真结果如图7～图10所示。

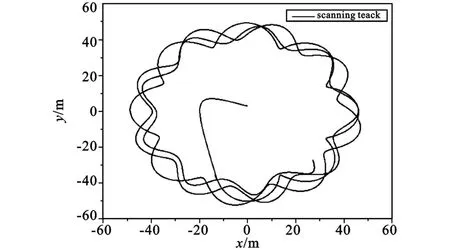
图7 末敏弹0～5 s扫描轨迹线Fig.7 The 0～ 5 seconds＇scanning track of terminal-sensitive projectiles

图9 末敏弹20～40 s铅垂平面扫描轨迹线Fig.9 The 20 ～ 40 seconds＇scanning track on plumb plane of terminal-sensitive projectiles plumb plane

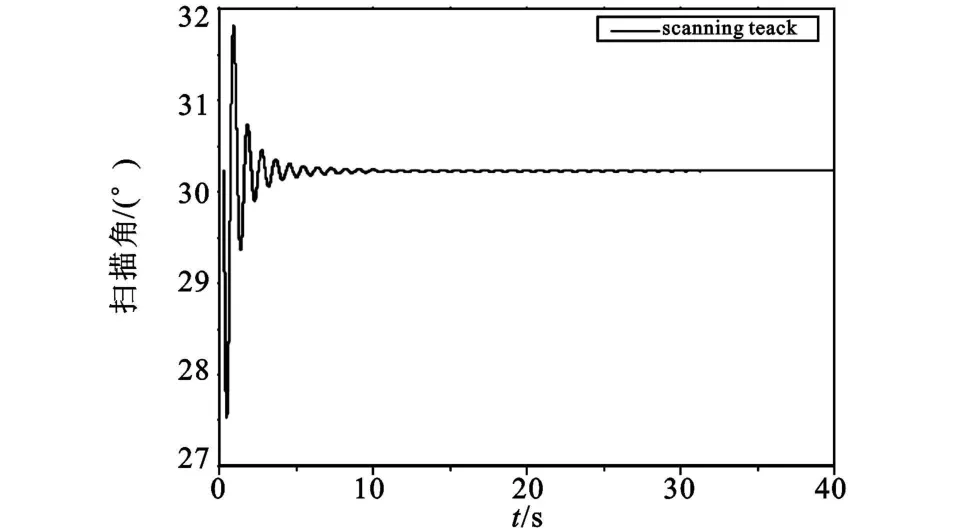
图10 末敏弹扫描角变化Fig.10 Scanning angle of terminal-sensitive projectiles changewith time

由图7可以看出,该伞弹系统的稳态扫描时间稳定得较好,0～5 s时的扫描曲线看上去虽然仍很紊乱,但已有趋于稳定的趋势。

由图8可以看出,在20～30 s,伞弹系统已经完全进入了稳态的扫描阶段,扫描曲线为等间距的螺纹线,并可直接从图上读出该扫描间距为1.48 m。

图9为末敏弹在铅垂平面上的扫描轨迹,此扫描轨迹线看上去类似一个等腰三角形,如果从空间上看去,则该扫描轨迹线为一圆锥体。如果以20 s时进入稳态扫描阶段。则由图9可以看出,该末敏弹的扫描面积约为7 850 m2。

由图10可以看出,大约在5 s时子弹的扫描角便已趋于稳定。

5 结论

本文针对末敏弹在采用降落伞和其他气动力机构(采用单翼或双翼)稳态扫描时的缺点,提出了一种降落伞和尾翼相结合的布局形式。这种布局形式通过在子弹尾部安装三片尾翼,可在稳态扫描时为子弹提供一定的阻力,减小携带降落伞的尺寸,提高了末敏弹的作战效果。通过对子弹进行气动仿真和弹道分析,表明该布局形式的可行性,可用于下一步的末敏弹武器系统研制中。

[1]杨启仁,耿茂盛.子母弹抛撒动力学模型[C]//中国兵工学会弹道学术交流论文集.厦门:中国兵工学会弹道专业委员会,1992:498-502.

[2]陈廷楠,张登成.双欧法与四元数法的应用比较[J].飞行力学,1996(12):59-64.CHEN Tingnan,ZHANG Dengcheng.Application comparision of dual Euler method and quaternion method[J].Flight Dynamics,1996(12):59-64.

[3]黄雪樵.克服欧拉方程奇异性的双欧法[J].飞行力学,1994(12):28-37.HUANG Xueqiao.The Dual Euler method for Overcoming the Singularity of Euler Equation[J].Flight Dynamics,1994(12):28-37.

[4]周伟,张晓今,寇保华.双欧法在克服伞-弹系统欧拉方程奇异性中的应用[J].航天返回与遥感,2003(9):4-8.ZHOU Wei,ZHANG Xiaojin,KOU Baohua.The application of the dual-euler method for overcoming the singularity of euler equation in parachute-missile system[J].Spacecraf t Recovery&Remote Sensing,2003(9):4-8.