反鱼雷方案对抗效能定量评价模型

高学强,杨日杰,张林琳

(1.海军航空工程学院信息融合技术研究所,山东烟台 264001;2.解放军71799部队,山东淄博 255300)

0 引言

关于潜艇如何使用水声对抗器材对来袭鱼雷进行对抗及其效能评估,国内外学者已进行了一些研究[1-3],得出了一些定性分析结论,但没有给出具体的仿真模型,且评估模型的可操作性不强,仿真应用存在一定的局限性,对反鱼雷方案不能给予有效的定量评价。为此,本文提出了利用蒙特卡洛法仿真的效能评价模型。

1 反鱼雷方案

当潜艇发现鱼雷入水之后,应立即释放水声对抗器材,然后潜艇加速、转向以及下潜。首先发射一对干扰器和诱饵,诱饵的航向设置为和鱼雷的航向垂直,第二组干扰器在一定时间后被发射出管,然后潜艇转为诱饵的相反方向并以最大速度进行规避[1]。干扰器可在潜艇周围形成声探测的屏障以中断鱼雷对潜艇的接触,然后声诱饵把鱼雷诱骗到距离潜艇的较远位置。

根据来袭鱼雷的位置,对抗初期的态势可分为前方右舷鱼雷报警、前方左舷鱼雷报警、后方左舷鱼雷报警、后方右舷鱼雷报警四种情况。以潜艇的初始位置为坐标原点S,初始航向为X负半轴建立直角坐标系,假设鱼雷自第二象限来袭,在距离潜艇1 500m的位置T入水,如图1所示。

图1 前方右舷鱼雷报警对抗态势Fig.1 the countermeasure situation of the torpedo coming from frontage and right side

对于每种态势,潜艇在转向和声诱饵的投放上都有不同的对策。当接近的鱼雷在象限II时,此时鱼雷在潜艇右舷,把声诱饵投放到象限I并取垂直于鱼雷方位作为其航向,潜艇则加速并左转进入第Ⅲ象限,航向为远离诱饵方向,这样可以保持声诱饵和鱼雷在它的尾部。

2 对抗效能模型

2.1 潜艇的机动规避模型

设潜艇的初始航向为θS0,初始航行速度为V S0,初始位置坐标为(x S0,y S0),转弯半径为R S,转弯时的速度为V S,转弯角速度为ωS,加速度为a,Δθ为规避需要作的转向角度,θS为规避后的航向,R为潜艇对鱼雷的可靠预警距离,鱼雷报警时鱼雷的位置为(x T0,y T0),鱼雷的来袭方向角为β,诱饵的初始航向角为θD,潜艇规避时不作超过90°的转向,潜艇需要作的转向角度为:

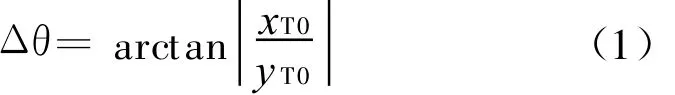
前方右舷鱼雷报警时,潜艇直航时航向角为:

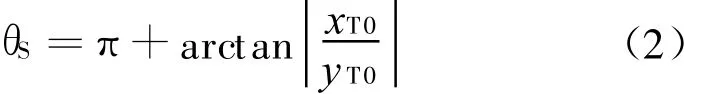
自航式声诱饵的初始航向为:

潜艇规避加速转弯前的运动轨迹:

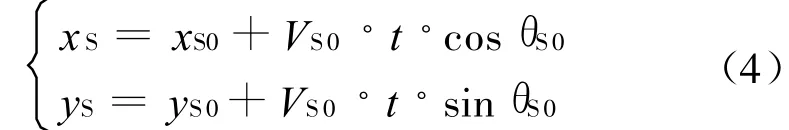
令(xm,y m)为潜艇转弯时的圆心坐标,转弯时潜艇的运动轨迹为:

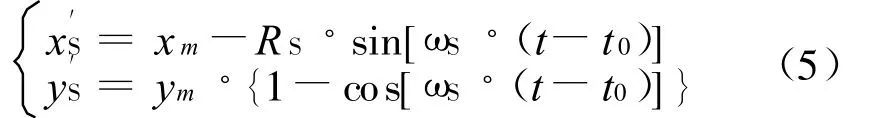
潜艇规避后的运动轨迹为:

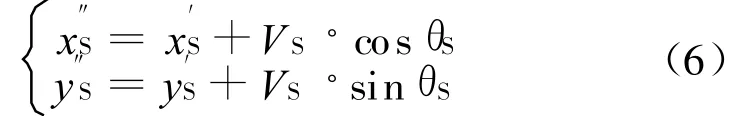
由上述模型可模拟计算对抗过程中潜艇任一时刻的位置坐标。

2.2 噪声干扰器的对抗模型

设潜艇发射第一组干扰器的时间为t J1,发射第二组干扰器的时间为t J2,发射干扰器时潜艇自身的位置为(xtJi,ytJi),假设潜艇发射完对抗器材后才进行机动规避,则两组干扰器位置坐标可近似为(xtJi,y tJi±40),其中i=1,2。

2.3 自航式声诱饵的对抗模型

设诱饵的速度为V D,潜艇发射诱饵的时刻为tD,潜艇发射诱饵时的位置坐标为(xtD,ytD),则诱饵的运动轨迹为:

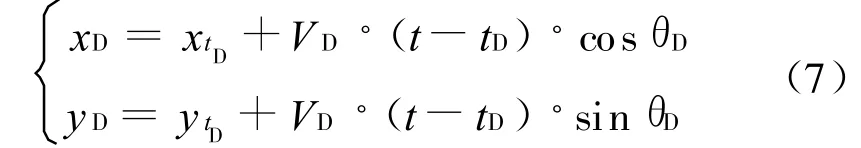
这里假设诱饵的弹道是直航,不考虑二次转角等比较复杂的情况。

2.4 鱼雷的搜索和攻击模型

假定鱼雷的搜索弹道采用环行方式,追踪弹道采用尾追式。当鱼雷丢失目标进行再搜索时,采用环行搜索[4]。

1)环行弹道

设鱼雷自tc时刻于(Xc,Yc)点以CTc航向开始环行搜索,环行角速度 ωT(左旋为正,右旋为负),则以开始环行点为原点,以该时刻鱼雷航向为y1轴建立直角坐标系(x1O1 y1),如图2所示。

图2 鱼雷环形弹道示意图Fig.2 The schematic diagram of torpedo＇s annular trajectory

设鱼雷旋回半径为RT=|VT/ωT|,则旋回圆心坐标为:

对于鱼雷环行航行任一时刻t1,有旋回角度

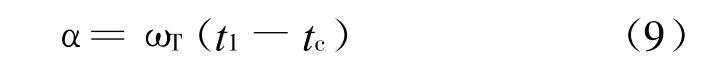
鱼雷在t1时刻的位置及航向为:

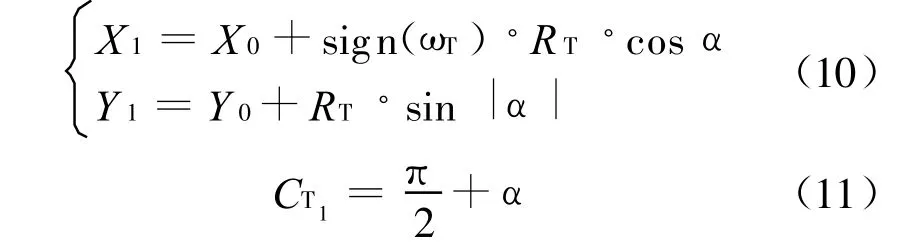
根据上面结果,通过坐标变换,即可得到鱼雷在原坐标系中的位置(X,Y)和航向CT。

2)尾追式弹道

设ti时刻鱼雷位于(Xi,Y i),航向C Ti,首先计算下一次操舵鱼雷应取的航向C Ti+1,或者是鱼雷航向在一个检测周期Δt内的改变量ΔCTi,则经过下一次操舵后,鱼雷到达的位置为:

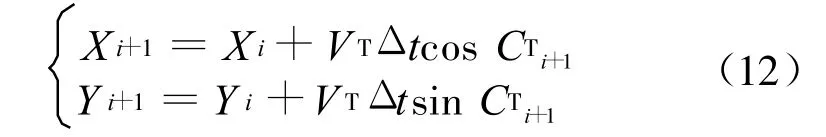
3)再搜索弹道

如果鱼雷环行搜索一周后仍发现不了目标,则按照选择逻辑中潜艇的最初位置信息,沿着目标的方向进行环行搜索。设鱼雷重新开始环行搜索的位置为(xTL,yTL),关于目标的存储位置信息为(xSL,y S L),则根据两者位置关系,可求出鱼雷环行搜索一周后下个圆周的圆心坐标(x Ti,y Ti),然后利用环行弹道的计算公式即可求出鱼雷的运动轨迹。

3 蒙特卡洛仿真

假设鱼雷的初始位置是在以潜艇为中心,半径为1 500 m范围内随机选取的,其相对潜艇的方位在 0°～ 360°范围内 。

对仿真进行如下假定:

1)假设只有1枚鱼雷来袭,且潜艇在鱼雷入水的同时可准确发出报警信息;

2)假设潜艇为常规潜艇,装备有1枚自航式声诱饵和4枚干扰器,且工作性能完好;

3)假定噪声干扰器可中断鱼雷对我艇的接触;

4)假定声诱饵发射后,鱼雷立即跟踪声诱饵,当识别出为假目标后,不再对其进行二次追踪;

5)不考虑潜艇能源的限制,潜艇可在一定时间内进行各种战术动作。

采用蒙特卡洛法进行仿真,仿真次数10 000,随机因素为鱼雷报警距离的误差,假设在(0,200 m)服从均匀分布,模拟统计潜艇未被鱼雷捕获的次数,即可得到不同方案参数时反鱼雷方案的对抗效能。

1)潜艇规避速度对其生存概率的影响

假设潜艇的初始航行速度5 kn,规避的最大速度范围为12～24 kn,以鱼雷报警的时刻为时间起点,鱼雷续航时间为终点。鱼雷报警后潜艇立即发射第一组干扰器,经过10 s时间的决策然后发射声诱饵,经过4 s再发射第二组干扰器,然后潜艇进行机动规避,其余参数按照2节描述设定,可得潜艇规避速度对其生存概率的影响情况如图3所示。

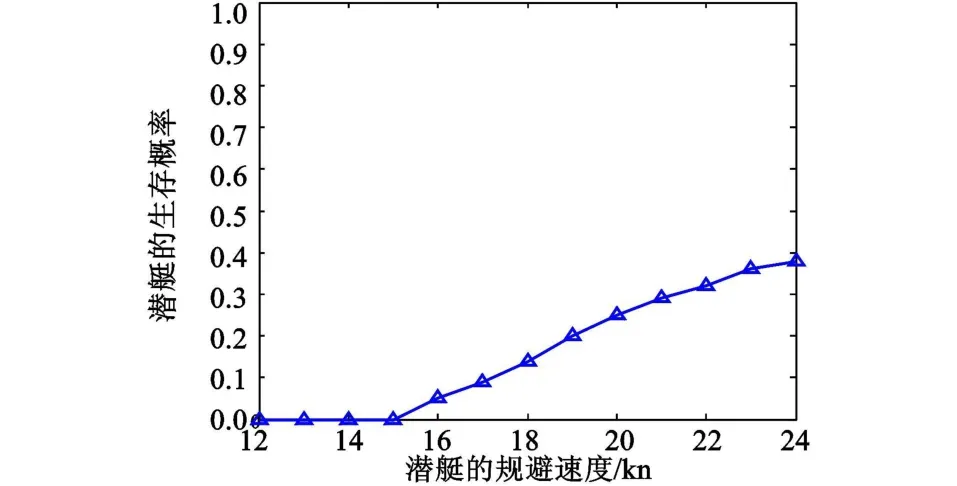
图3 潜艇规避速度对其生存概率的影响Fig.3 The effect of submarine＇s evasion speed on its survival probability

可见:当潜艇的规避速度低于16 kn时,其生存概率为0,说明此时该对抗方案是失败的。当潜艇的规避速度在16 kn以上时,随着速度的增加,其生存概率迅速增加。这表明了潜艇的最大航行速度对于整个对抗方案的重要性。

2)潜艇规避时机对其生存概率的影响

假设潜艇的规避速度为20 kn,其他参数和上节相同,规避时刻为发射完第二组干扰器以后的任意时刻,则经模拟统计,可得潜艇规避时机对其生存概率的影响情况如图4所示。

图4 潜艇规避时机对其生存概率的影响Fig.4 The effect of submarine＇s evasion time on its survival probability

可见:潜艇规避的时间越晚,潜艇的生存概率越低。当潜艇的规避时刻大于3 min时,由于鱼雷在跟踪识别出诱饵为假目标后又重新锁定了目标,此时潜艇已经很难摆脱鱼雷的攻击。因此,潜艇在发射完对抗器材后,应马上进行机动规避。

3)自航式声诱饵的航速对其生存概率的影响

假设潜艇的规避时刻为发射完第二组干扰器以后立即转向加速,声诱饵的发射时刻为鱼雷报警后10 s,航速变化范围为15～25 kn,其他参数和上节相同,则经模拟统计,可得诱饵航速对潜艇生存概率的影响情况如图5所示。

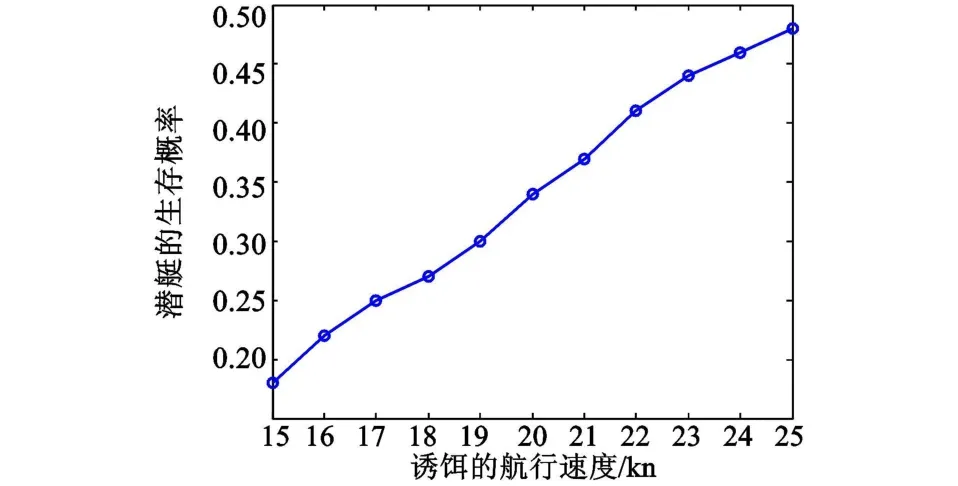
图5 诱饵的航速对其生存概率的影响Fig.5 The effect of decoy＇s speed on submarine＇s survival probability

可见:随着诱饵航速的增加,潜艇的生存概率迅速增加;和潜艇的规避速度比较而言,诱饵的航速对潜艇的生存概率影响更显著。这是由于鱼雷在跟踪诱饵的过程中,诱饵的速度越高,鱼雷追上识别诱饵的时间越久,同时鱼雷距离目标的距离也会越远,其航程也消耗的越长。因此,就诱饵的续航时间和航速来说,航速对对抗效果的影响更为显著。

4)自航式声诱饵的发射时机对其生存概率的影响

设诱饵航速为17 kn,考虑到诱饵发射须在干扰器对鱼雷实施干扰之后,且必须有一定的决策和反应之间,因此声诱饵的发射时刻为鱼雷报警10 s以后,其他参数和上节相同,则经模拟统计,可得诱饵发射时机对潜艇生存概率的影响情况如图6所示。

可见:诱饵发射的时间越晚,潜艇的生存概率越低;和潜艇比较而言,诱饵的发射时机对潜艇的生存概率影响更显著。当诱饵的发射时刻大于 110 s时,鱼雷此刻已经距离潜艇和诱饵都很近,鱼雷可以很快的识别出诱饵为假目标,然后重新跟踪潜艇,因而对抗效果很差。因此,潜艇在发射完干扰器后,应利用干扰器对潜艇的屏蔽作用,立即施放诱饵。

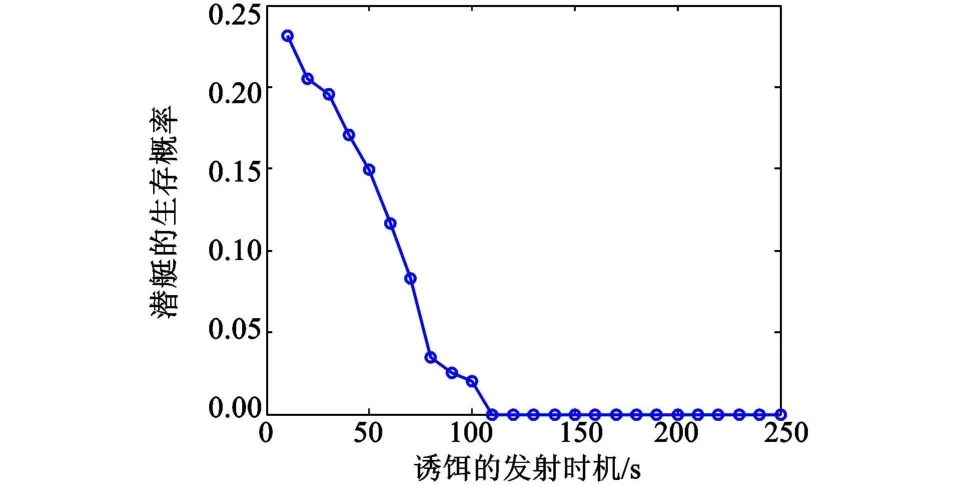
图6 诱饵的发射时机对其生存概率的影响Fig.6 The effect of decoy＇s launched time on submarine＇s survival probability

4 结论

本文提出了潜艇反鱼雷方案的对抗效能定量分析模型,包括潜艇的机动规避模型、噪声干扰器的对抗模型、自航式声诱饵的对抗模型、鱼雷的搜索和攻击模型等。蒙特卡洛仿真表明,该模型可对潜艇反鱼雷方案进行定量评价,并且与定性分析结果吻合。该模型可以用作反鱼雷方案对抗效能的定量分析,为进一步深入研究反鱼雷对抗方案的效能评估问题提供了参考。

[1]Armo K R.The relationship between a submarine＇s maximum speed and its evasive capability[D].Monterey CA:Operations Research Department,Naval Post-graduate School.

[2]贾跃,宋保维,梁庆卫.火箭助飞声诱饵对抗鱼雷的舰艇规避优化模型及其生存概率分析[J].兵工学报,2008,29(5):637-640.JIA Yue,SONG Baowei,LIANG Qingwei.Evadable optimization model and survival probability analysis of warship with rocket assist acoustic decoy countering torpedo[J].Acta Armamentarii,2008,29(5):637-640.

[3]贾跃,宋保维,崔绍波.助飞声诱饵对抗声自导鱼雷数学模型及其仿真[J].系统仿真学报,2008,20(2):267-269.JIA Yue,SONG Baowei,CUI Shaobo.The mathematical and simulation model of countering the acoustic homing torpedo with the acoustic decoy[J].Journal of System Simulation,2008,20(2):267-269.

[4]孟庆玉,张静远,宋保维.鱼雷作战效能分析[M].北京:国防工业出版社,2003.