基于混沌机制PID控制器优化设计的研究
2010-08-23陈雯柏刘景伟
陈雯柏,张 鹏,刘景伟
CHEN Wen-bai1, ZHANG Peng2, LIU Jing-Wei3
(1. 北京信息科技大学 自动化学院,北京 100192 2. 河北建材职业技术学院 信息机电系,秦皇岛 066000;3. 国电大渡河公司龚嘴水力发电总厂,乐山 614900)
0 引言
PID控制器结构简单、易于实现,并具较强的鲁棒性,被广泛应用于各种工业过程控制中。PID控制器参数整定优劣与否,是其能否在实用中得到好的控制效果的前提。自Ziegler和Niehols提出PID控制器参数经验公式法起,有很多方法己经被用于PID控制器的参数整定[1~4]。这些方法可按发展阶段分为常规参数整定方法及智能参数整定方法。先进PID控制器参数整定方法给PID控制的研究带来了活力。
PID参数整定实质是一组参数优化问题,选择一个合适的算法,根据系统的性能目标函数,就可寻优到合适的PID参数。混沌是存在于非线性系统中的一种较为普遍的现象,混沌运动具有遍历性等特点 ,它能在一定的范围内按其自身规律不重复地遍历所有状态。本文采用梯度下降和混沌搜索相结合,完成PID控制器参数优化并成功应用于磁悬浮球控制系统。
1 混沌优化PID控制器设计
1.1 混沌优化
基于混沌理论的优化是一种新型的优化算法,它直接采用混沌变量在允许的解空间中进行搜索,搜索过程按混沌运动的自身规律进行,具有随机性,易于跳出局部最小值,搜索效率高。因此,将混沌理论应用于控制系统的优化搜索中是近年来不断探讨的热点问题[4,5]。
混沌优化算法的基本思想就是把混沌变量线性映射到优化变量的取值区间,然后利用混沌变量进行搜索。著名的Logistic(倍周期分岔道路)映射系统是目前研究的最深入的一个混沌系统模型,其动力学方程如式(1)所示:

这里µ是一个控制参数,当µ大于3.57后,系统(1)开始出现混沌;当µ=4时,则完全处于混沌状态,混沌变量x在(0,1)范围内遍历。混沌优化算法的特点是:1)结构简单,有较高的执行效率;2)遍历性特点中避免搜索过程陷入局部极小;3)不需要知道目标函数的导数信息;4)具有较少的计算量和较快的求解速度,调节参数可灵活控制计算时间和精度。
2.2 PID控制器参数寻优
PID参数整定实质是一组参数优化问题,选择一个合适的算法,根据系统的性能目标函数,就可寻优到合适的PID参数。寻求PID控制最优参数是按照一定的寻优策略,不断探测、调整,自动寻找最优的数字PID控制器参数,使得系统状态处于最优状态。PID控制器参数优化方法主要有以下两种途径:
1)基于现代控制理论的整定方法,写出目标函数的解析式,然后根据目标函数取极值的充分必要条件,求出控制器参数的最优解。
2)基于一定的寻优算法,直接在参数空间中遍历寻得最优参数值。
混沌PID参数寻优便属于第二种途径,其基本思想是:结合控制系统稳定的附加条件,利用混沌变量进行全局优化搜索PID参数最优解。用于PID控制器参数整定,寻优的目标函数必须与系统调节的性能指标函数密切相关,反映系统的调节品质。描述控制系统的目标函数并不是唯一的,常用的误差性能目标函数有IAE、ISE及ITSE等[4]。
2.3 混沌PID控制器参数寻优算法
离散增量式PID表达式为:
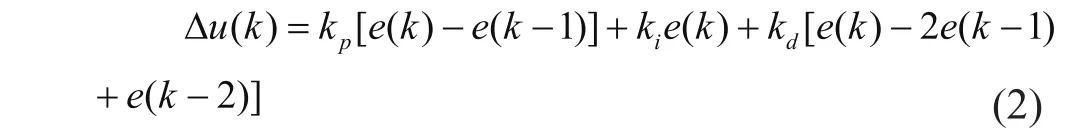
其中,T为采样周期;k为采样序号,k=1,2,...,N;u(k)为第k次采样时刻PID控制器输出的控制量;e(k)、e(k-1)分别为第k、(k-1)次采样时刻输入的偏差值;为积分系数,。由于混沌变量的变化范围为(0,1),而PID参数的变化不完全是(0,1)。可按式(3)所示进行变换将混沌变量映射“放大”为优化参数变量

混沌优化具有全局搜索能力,但其局部搜索能力稍显不足。基于梯度方向的确定性方法,虽具有收敛速度快的特点,但又容易陷入局部极值。因此采用混合优化算法先最速下降,再混沌搜索进行有机结合。为进一步提高搜索速度,文献[6]提出一种改进的变尺度混沌搜索算法,本文应用并改动如图1所示。实现尺度变换控制搜索半径, λ控制变换的幅度。
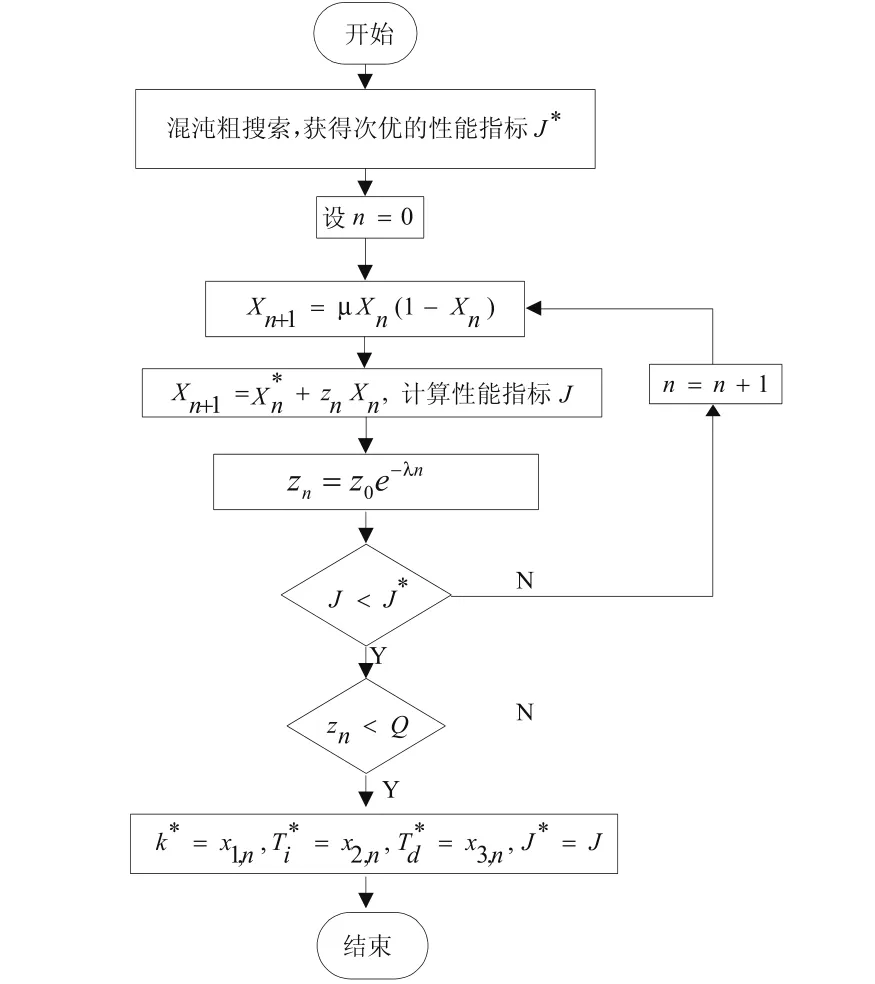
图1 混沌优化算法的计算步骤
3 磁悬浮球系统的混沌优化PID控制
作为研究磁悬浮技术的平台,磁悬浮球系统是一个典型的吸浮式悬浮系统,由铁芯、线圈、位移传感器、控制器、功率放大器和钢球等元器件组成,其控制目标是通过调整加在电磁铁线圈中的电流变化量i,使钢球无接触地稳定悬浮在空中。本文所研究磁悬浮球系统结构图如图2所示[7,8]。

图2 磁悬浮球实物系统结构
实际磁悬浮球系统的模型参数如下:钢球质量m=22g,浮球半径r=12.5mm,铁芯直径=22mm。忽略漏磁通,并假设磁通在气隙处均匀分布,忽略小球和电磁铁铁芯的磁阻,假设球所受的电磁力集中在中心点,同时忽略小球受到的其他干扰力,在小球平衡点附近进行线性化处理。定义系统对象的输入量为功率放大器的输入电压也即控制电压Uin,系统对象输出量为 所反映出来的输出电压Uout(传感器后处理电路输出电压),则该系统控制对象的模型可写为:
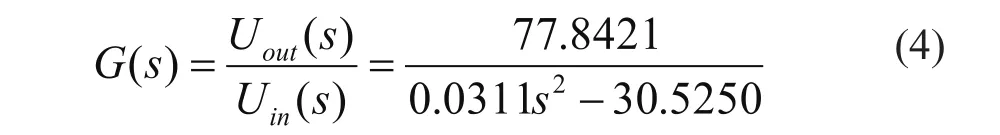
基于Matlab / Simulink的磁悬浮球实时控制系统结构如图3所示,系统采样周期T为0.003s。图的左边Pos Ref模块给定了钢球位置,通过Scope等模块可以查看系统实时控制效果。
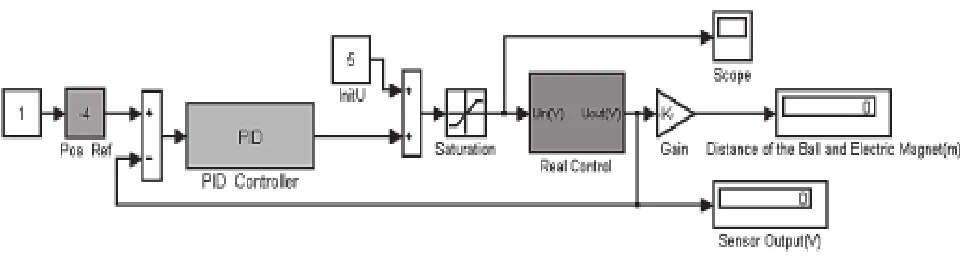
图3 磁悬浮球系统的实时控制平台
设定小球平衡位置为-1cm,采用传统PID参数整定方法可得:kp=0.5,ki=0,kd=3,小球实际位移变化曲线如图4(a)所示;在此基础上,运用上述参数寻优方法得到的参数为:kp=0.4090,ki=0.000065,kd=4.1098,小球实际位移变化曲线如图4(b)所示。

图4 小球实际位移曲线比较
由图4比较可知,在给定相同的位移 -1cm的情况下,采用混沌优化PID控制参数寻优后稳态误差小,位移波动量也较小,取得了较好控制效果。这说明基于混沌优化方法的PID控制器设计是可行的。
3 结束语
混沌运动具有遍历性特点,可应用于PID控制器的参数优化设计。本文首先对混沌优化的原理进行了简单的介绍。接着,介绍了混沌PID控制器的参数优化设计的具体方法并进行了仿真研究。最后,针对实际的磁悬浮系统实验设备,设计了PID控制器,并对优化前后进行了比较分析。本文说明了基于混沌机制的PID控制器参数优化策略可行且效果良好。
[1]刘乐星,毛宗源.水轮机的GA-PID控制器研究[J],电力系统自动化,Dec 1997,21(12):41-43.
[2]K.H.Ang,G.Chong,and Y.Li.PID Control System Analysis,Design and Technology[J].IEEE Trans.on Control System Technology,2005,13(4):559-576.
[3]Wang P,Kwok D P.Auto-tuning of classical PID controllers using an advanced genetic algorithm[C],Proc.of IEEE Int.Conf.on Power Electronics and Motion Control,San Diego,1992:1224-1229.
[4]李丽香,彭海朋,王向东,杨义先.基于混沌蚂蚁群算法的P I D控制器的参数整定[J].仪器仪表学报,2006,27(9):1104-1106.
[5]李祥飞,邹恩,张泰山.基于混沌优化的规范化PID控制器及其应用[J].中南工业大学学报,2002,33(3):301-304.
[6]邹恩,陈建国,李祥飞一种改进的变尺度混沌优化算法及其仿真研究.系统仿真学报,2006,18(9):2426-2428.
[7]固高科技.GML系列磁悬浮系统实验指导书[Μ].深圳:固高科技(深圳)有限公司,2006.
[8]许良琼,陆新江,李群明.模糊PID控制在磁悬浮平台中的应用[J].中南大学学报(自然科学版):2005,36(4):631-636.
