解析位移反分析法在隧道工程中的运用

冯小晗

1 工程概况

某铁路越岭隧道在施工过程中,围岩呈现出软岩的性质,在许多地段发生了大变形现象,给正常施工带来了很大的影响:由于围岩成孔性差,不便操作,以至于对是否属于高地应力,是否存在较大的水平构造应力的判断带来了直接影响;洞室开挖后变形长期不收敛,塑性区的测设由于弹—塑性区不存在明显的分界面,现场测量有很大的难度;现行的数值模拟技术大多基于小变形假设,施工过程的模拟值与实际结果出入较大。影响岩体二次应力状态因素很多,如岩体的初始应力状态,岩体的构造,洞室的形状尺寸,洞室的埋深和开挖施工技术等。解析法推导基于下述假定:岩体为均质的、各项同性的连续介质;考虑自重应力和构造应力形成的初始应力场;洞室形状为圆形;洞室位于一定的深度,简化为无限体中的孔洞问题。在传统的岩石工程理念中,洞室埋深较浅,自重应力P0一般为大主应力,水平应力的计算为λ P0(λ＜1),一些理论解析方法都是建立在这个基础上的。进入21世纪以后,随着经济、科技、理念的进步,岩石工程的埋深已经突破地下3 000 m,其大、小主应力的值、方向与以往的理论计算有一定的差别。在下面的推导中,水平力为大主应力,自重引起的应力一般为小主应力或中间主应力。

2 圆巷围岩的弹性应力和变形状态

2.1 圆巷围岩的弹性应力解

假设圆巷的水平荷载对称于竖轴,竖向荷载对称于横轴;竖向力为 P0,横向力为λ P0(λ＞1)。由于结构本身对称(荷载不对称),上述问题运用叠加原理解决,见图1。

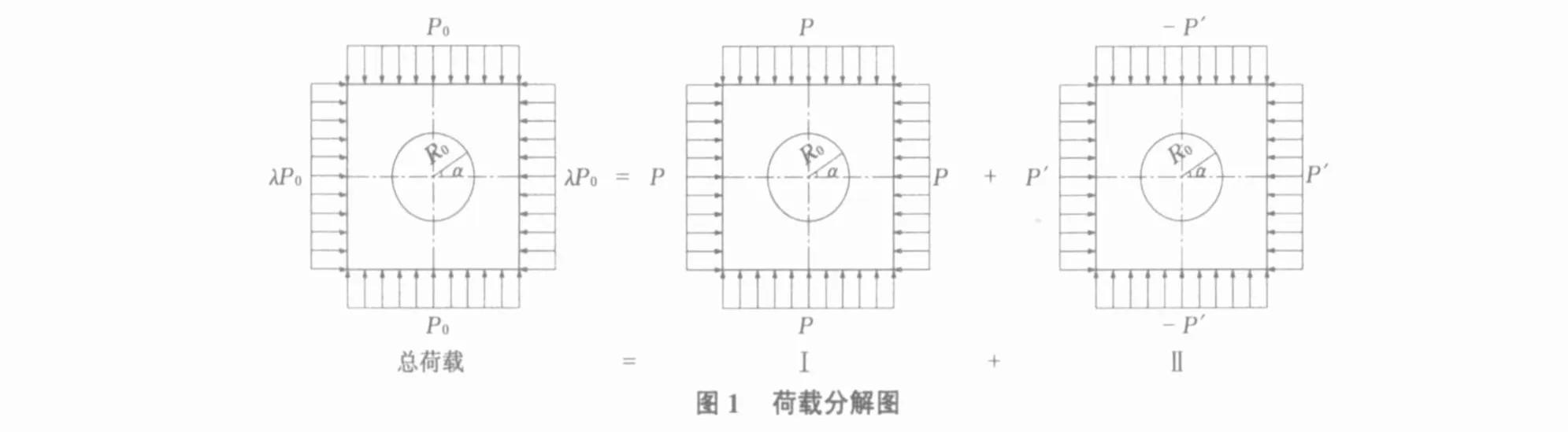
将荷载可分解为:

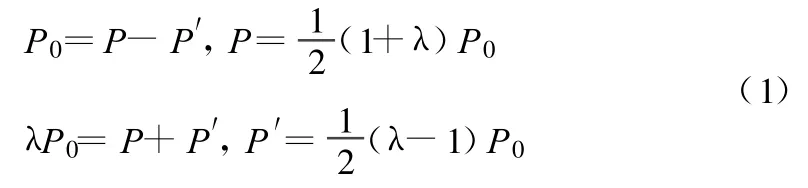
则上述一般圆巷的弹性应力状态为荷载分解后的两种情况的叠加。

1)情况Ⅰ的解。因为是轴对称问题,由弹性力学的结论得出情况Ⅰ的应力解[1]:

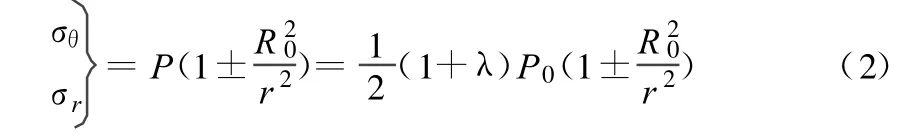
2)情况Ⅱ的解。对于内边界 r=R0,σr=σrθ=0;对于外边界,应用摩尔圆应力关系,有:

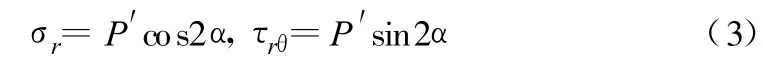
通过选定应力函数,求解双调和函数,代入边界条件即得情况Ⅱ的解:

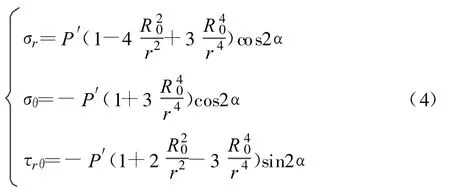
综合情况Ⅰ和情况Ⅱ的应力解:

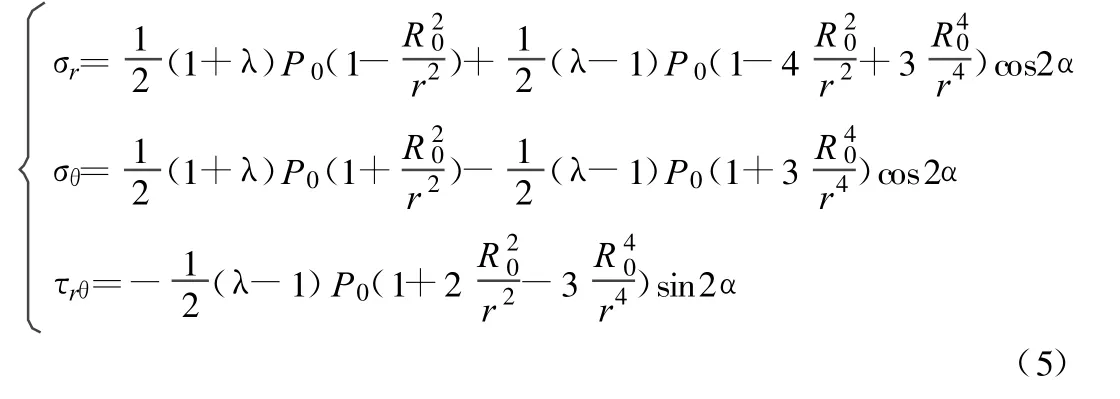
2.2 圆巷围岩的弹性位移状态

圆巷开挖产生应力释放而引起的释放位移可以这样考虑:在平面应变问题中,首先运用应力—应变关系,求得r处圆巷开挖后的相对径向位移,同时减去圆巷开挖前 r处的径向位移值,即可得到圆巷开挖后r处的径向释放位移:

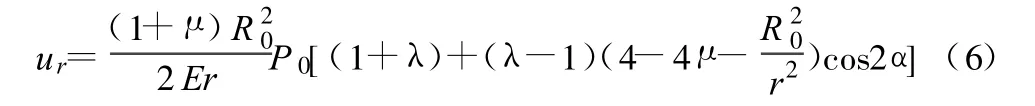
3 圆巷开挖后塑性区的应力和位移状态

塑性区几何半径可以对鲁宾涅特方程加以修正,总塑性区半径rP=轴对称塑性区半径RP+与a有关的塑性区半径RPf(a),斜直线型强度条件塑性区半径计算式为:

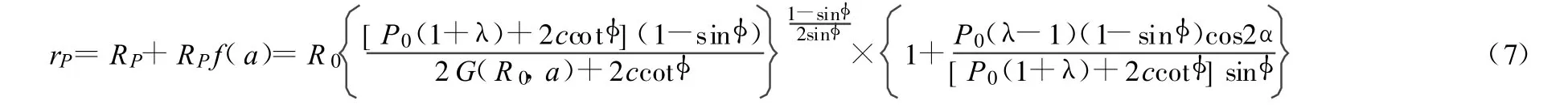
圆巷弹塑性位移:一般圆巷弹塑性位移计算通式为[3]:

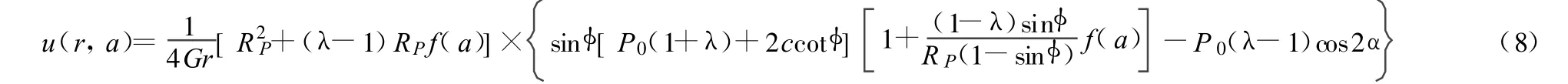
4 解析法在隧道工程中的运用

运用物探方法和室内试验测得岩性力学指标 γ=20 kN/m3,u=0.35,φ=35°,C=0.7 MPa;铅锤方向只考虑自重应力影响;隧道开挖半径为5.28 m。图2为不同里程实测水平变形弹性值和拱顶下沉弹性值。

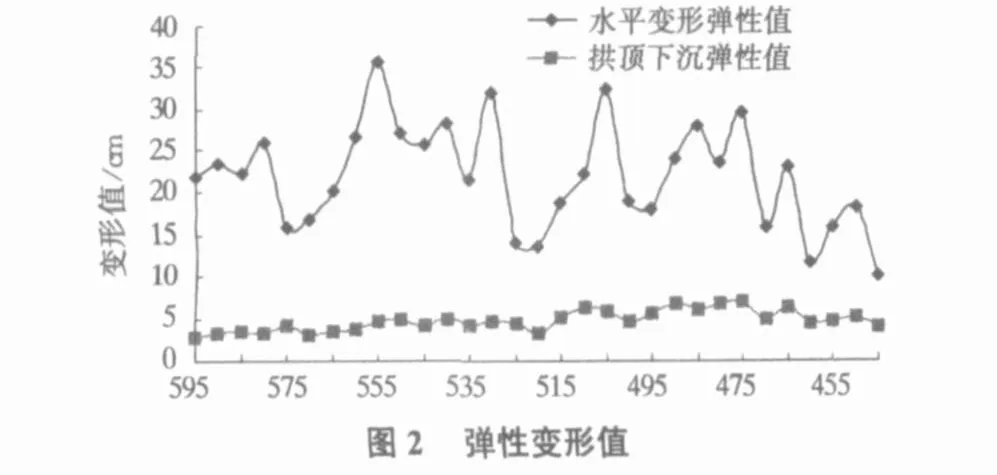
经反算得出:λ=1.66,E=967 MPa;塑性区内最大应力、塑性区大小、隧道开挖后的最终变形量见表1,其中,支护抗力的大小由围岩与初期支护间接触压力确定。

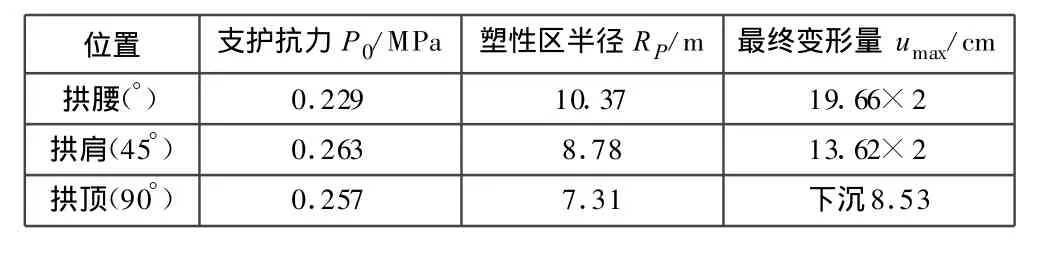
表1 不同位置的计算值

5 结语

通过洞室开挖后弹—塑性解的推导,并结合工程实际,表明隧道发生大变形主要受岩性、应力场分布、断面形式等因素影响。在发生变形地段,水平最大变形值超过60 cm,拱顶下沉超过30 cm,且长时间不收敛,与解析值有较大差别,表明初期支护体系需要加强和尽快闭合,尤其钢支撑接头处等关键部位;系统锚杆应当穿过塑性区,锚固于较为稳定的围岩中;及时衬砌是处理工程软岩的重要环节。

[1] 吴家龙.弹性力学[M].上海:同济大学出版社,1987.

[2] 冯卫星,吴康保.铁路隧道设计[M].成都:西南交通大学出版社,1998.

[3] 蔡美峰,何满潮,刘东燕.岩石力学与工程[M].北京:科学出版社,2002.