声基阵网络节点被动式时间同步与定位方法

邱扬刚,张 亚,李世中

(中北大学机电工程学院,山西太原 030051)

0 引言

国外对传感器无线组网的研究起步较早,其巨大的军事应用价值得到世界上许多国家的极大关注[1]。其中被动声传感器网络的优点使其在战术防空中可用于复杂地形地区的低空预警和雷达补盲。单个的被动声基阵探测范围小,对动目标的探测和预警能力有限,信息很难共享,而被动声传感器基阵网络的信息化能力和感知探测能力则有质的提高,具有可快速部署、可自组织、覆盖区域大、隐蔽性强和高容错性等优点,因此极具应用前景。而其研究难点之一就在于声传感器区域无线组网技术。

在无线组网技术中,目前已有的基于距离的节点定位方法主要为基于时间到达的TOA定位、基于到达时间差的 TDOA定位、基于到达角度的AOA定位和基于接收信号强度指示的RSSI定位[2]。TOA定位和TDOA定位要求精确的时间同步,利用距离信息和相应算法完成节点定位,对硬件的要求较高,成本高;AOA定位以TOA定位为基础,利用天线阵列感知方位角,通过三角测量法完成节点定位[3],该技术复杂、通信量大、能耗高;RSSI定位则不适用于复杂开阔的外部环境。针对以上节点定位方法的缺点和不足,本文提出被动式时间同步机制与网络节点的被动声基阵定位方法。

1 网络节点模型

声学定位模型设计是被动声定位的关键技术之一。五元空间被动声探测基阵的优点是定距精度高、定向精度与方位角无关、俯仰角对定距精度的影响较小,应用于动目标的被动声探测和节点定位较为理想[4]。

被动声基阵无线网络的节点定位机制中,节点的定位部分由扬声器、五元声传感器基阵、处理器模块和无线通信模块组成,如图1所示。

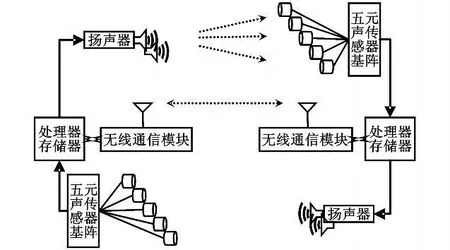
图1 五元空间被动声探测基阵网络节点定位图示Fig.1 The five-element space detection array network node localization model

五元空间被动声探测基阵网络包含任务节点、信标节点以及管理终端,大量的声基阵节点随机部署在监测区域内,通过自组方式构成网络。任务节点检测的数据经处理模块处理后沿路由路径节点逐跳地进行传输,经多跳后路由到信标节点,最后通过管理终端传输给用户。每个任务节点兼有传统网络节点和路由器双重功能,除进行监测区域的信息收集和处理外,还要对其他节点转发来的数据进行处理和转发。信标节点是一个具有增强功能的传感器节点,有足够的能量供应、较大的内存和较强的计算能力,能独立完成自身的定位和授时,它的通信能力、存储能力、处理能力都要较任务节点强,它担负其他任务节点的位置定位、授时,它连接着一定数量的任务节点和管理终端,实现两种协议栈之间的通信协议转换,同时将收集的数据转发到管理终端。

2 网络节点被动声基阵定位

节点定位过程中不仅包括地理位置信息,还包括至关重要的时间信息[5]。在被动式时间同步机制下,利用本地时钟的时延值或时间差,节点的五元被动声基阵即可完成节点自身定位。

2.1 被动式时间同步机制

时间同步对网络的信息传输和交换具有重要意义。在传统网络中节点的定位离不开时间同步,因此提出了多种时间同步机制。NTP协议已广泛应用于互联网,具有易扩展、精度高的优点,但它依赖于有线的传输网络不适于无线传感器网络;无线广播报时系统在声传感器基阵网络中很难得到相应基础设施的支持,而且易受干扰破坏;GPS能为网络系统提供纳秒级精度的标准时间,也适于在地形复杂开阔的地域使用,但是需要较高成本的接收机,无法每个节点都配备,只能为少数的信标节点使用。而且我国没有GPS的主控权,使用的是降低精度的粗码,战时更是不可依赖。我国的北斗二代卫星导航定位系统投入使用后,我们可以得到精度更高和完全控制权的定位、授时服务,完全可以为关键节点定位授时。

无线传感器领域的三种基本时间同步机制RBS、TPSN 和 TINY/MINI-SYNC,适用于不同的传感器网络。RBS机制适合多跳网络,它用去除发送时间和访问时间的方法来提高时间同步精度。但在实际传感器网络中,需要多个簇之间有共同点进行比对,才能实现时间同步,这依赖于有效的分簇方法,需要交换多个同步消息,消耗较多的网络能量,并且随条数的增多而误差增大。TPSN时间同步协议能提供比RBS机制更高的同步精度,但其同步信息交换频繁,协议开销大,而且一旦根节点失效则整个网络将丧失时间同步信息。TINY/MINI-SYNC同步算法的前提是时钟频偏和相偏固定不变,这在实际网络中难以实现,较低成本的晶振很难保证其长时间的稳定,这个问题同样存在于以上两种机制之中,这就需要信标节点按一定的周期发送同步信息对时,这样既耗费宝贵的能量又占用通信通道,会对突如其来的目标信息的转发造成阻塞。

声基阵传感器网络的主探测器是五元空间声传感器基阵,在定位过程中需要本地时钟的时延值或时间差,而不必与信标节点严格地时间同步,该网络的时间原理如图2所示,每一个节点都有标识ID和本地时钟,节点的本地时钟无需与信标节点同步。信标节点通过GPS或北斗卫星定位系统获得精确的定位和授时,以此为网络的标准时间。图中目标事件发生未知时刻为T,T为信标节点接收到单跳任务节点发送的目标信息的时刻,Tn为信标节点接收到n跳任务节点发送的目标信息的时刻;t1为任务节点完成对声目标的探测、数据处理,并将数据发送给信标节点所需的时间,即任务时间延迟t1=ta+tb,其中ta为目标的声信号发出到达探测基阵所需的时间,由计算得到;tb为完成信号处理、数据发送所需的时间,由节点本地时钟测得;故t1可实际测得。t2～tn为n跳内每个路由节点完成数据处理、转发所需时间,由每个路由节点的本地时钟测得,因此在目标探测、数据处理和转发每个过程所耗费的时间均可测得。这样信标节点通过已知时刻对已知时间延迟相减,其结果为目标事件发生的时刻,即:

在节点定位不需时间同步的情况下,依据声传感器基阵网络的实际,使用无需严格同步的时间方式,称之为被动式时间同步方式。

图2 五元空间被动声探测基阵网络时间机制原理图Fig.2 The network time mechanism principles of the five-element space detection array

2.2 节点被动声基阵定位

在声传感器网络中,目标事件发生的位置和获取信息的节点位置是声传感器节点所监测信息中至关重要的信息,没有位置信息就无法获得目标的方位、高度、速度、航向等信息。声传感器节点随机布放在监测区域内以信标节点为中心进行有效地分簇,随机布放的声传感器节点除信标节点外无法知道自身位置,声传感器节点在布放后要能够完成自身定位,节点根据离自己最近的信标节点的位置,利用自身携带的声基阵传感器按被动声定位的方式和算法确定自身的位置。

声基阵节点的定位原理如图3所示,该基阵共有5个传感器,S0、S1、S2、S3和 S4分别在 x轴和 z轴、y轴和z轴构成的坐标平面内,距坐标轴的距离为l,以S0为原点建立直角坐标系。假设节点A(x,y),节点到原点的距离为r,声波以球面波进行传播,以地北为基准逆时针方向方位角为φ,τi(i=1,2,3,4)为节点的声信号到达传感器Si和S0的时间差。ri(i=1,2,3,4)为节点的声信号到达Si和S0的距离差,c为声速。则有:

图3 五元空间探测基阵节点定位原理图Fig.3 The node localization principles of the five-element space detection array

根据直角坐标系中两点间的距离公式可得节点A的位置极坐标(φ,r)的表达式为:

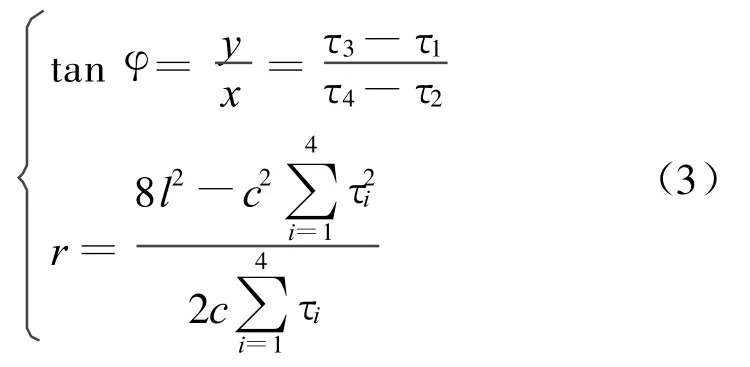
上述方程即为五元空间被动声探测基阵网络节点位置的定位方程。该五元空间基阵布阵有较好的定向精度和定距精度,方位角的误差与方位角和距离无关,在水平方向俯仰角对方位角和距离的影响较小。

被动声基阵网络中,信标节点在网络中所占的比例很小,配置较高。由北斗导航定位系统或GPS系统提供定位和授时,其他未知任务节点的参考坐标由信标节点通过无线通信方式发布自己的位置坐标(x,y),单跳距离的未知任务节点接收。信标节点的扬声器发出声信号,离信标节点单跳距离的未知任务节点利用五元声传感器基阵模块接收声信号,经处理后由定位公式(3)计算出信标节点相对自己的距离r和方位角φ,由两点换算公式(4)换算成自己的位置坐标:

在完成定位的同时,每个节点都会记录下自己的跳数,将得到的跳数信息和位置信息通过无线模块反馈给信标节点,最终传递给管理终端处理。单跳一级的节点按方位角 φ由小到大的优先级顺序,按上述方式对多跳未知节点进行定位。

3 节点定位误差分析

从定位公式来看,影响位置精度的因素有声速、时延估计、声阵尺寸和阵型的几何形状,为验证五元空间阵对节点的定位性能,下面对节点误差进行分析仿真,基于三个前提假设:

1)网络中节点处于同一水平面(在其他俯仰角情况下仍可利用声基阵测得,这里设节点处于水平面);

2)设节点距离的变化范围为0＜r≤200 m,有效声速为334 m/s(探测单元利用其他传感器探测风速、温度、湿度等值加以修正);

3)各声传感器时延估计的标准偏差相同,即:

3.1 方位角误差分析

在俯仰角θ=90°方位角估计的误差为:

节点定位的方位角精度与时延估计误差、声阵尺寸有关,与方位角和距离无关。方位角误差的仿真结果如图4所示。图 4为俯仰角 θ=90°时,方位角误差随时延估计误差和声阵尺寸变化的曲面图。

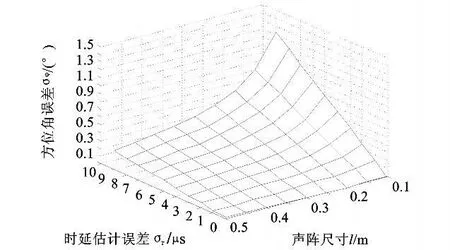
图4 方位角误差与声阵尺寸、时延估计误差关系图Fig.4 Azimuth error vs array size and time delay error diagram

从图4可以看出:时延估计误差取不同值时,方位角误差随声阵尺寸变化的曲线。当στ≤10μs,l≥0.2 m时 ,方位角误差σφ＜0.8°。当 στ≤5μs,时,方位角误差 σφ＜0.4°。

3.2 距离相对误差分析

在俯仰角θ=90°时,距离相对误差为:

距离相对估计误差与时延估计误差、阵列尺寸和节点间实际距离有关,与方位角无关。图5是俯仰角θ=90°时,距离相对误差随时延估计误差和声阵尺寸变化的曲面图。图中可以看出增大声阵尺寸和减小时延估计误差可以减小距离相对误差。当στ≤5μs,l≥0.2 m时,距离相对误差小于10%,当l≥0.5 m时,相对误差小于1.5%。

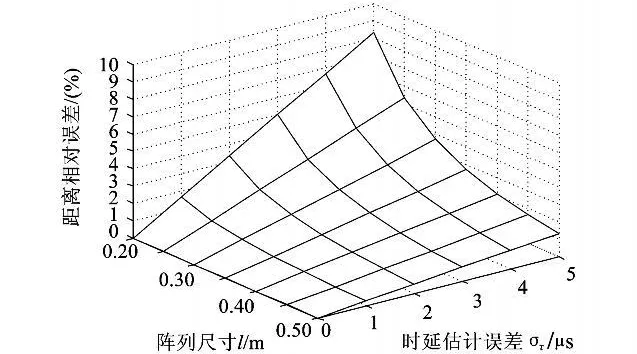
图5 距离相对误差与声阵尺寸、时延估计误差关系图Fig.5 Range relative error vs array size and time delay error diagram

图6 是当στ=5μs,l=0.5 m时,距离相对误差与距离的关系图。

图6 距离相对误差与距离关系图Fig.6 Range relative error vs range diagram

由图6可知,当要求距离相对误差为0.82%,即距离误差为1 m时,对应的节点距离为122 m。当r=200 m时,距离相对误差小于1.4%。而在500 m时的距离相对误差则约为3.5%。可见,在一定的时延估计误差和阵列尺寸下,声阵的测距精度随着目标距离的增大而下降,随距离的增加误差增大。

4 结论

本文提出了被动式时间同步机制下的网络节点被动声基阵定位方法,该方法在被动式时间同步机制下,利用本地时钟的时延值或时间差,节点的五元被动声基阵即可完成节点自身定位,其对硬件要求低,通信量小,节省能量开销。误差分析表明节点在有效的定位距离内精度较高,为网络路由协议、通信协议和数据融合处理提供研究依据。

[1]宋海涛,何明一,段渭军,等.基于无线传感器网络的声目标识别算法研究[J].电子测量技术,2007,30(12):63-69.SONG Haitao,HE Mingyi,DUAN Weijun,et al.Arithmetic research of acoustic objectives identification in WSN[J].Electronic Measurement Technology,2007,30(12):63-69.

[2]孙利民,李建中,陈渝,等.无线传感器网络[M].北京:清华大学出版社,2005.

[3]Dragos,Niculescu,Badri Nath.Ad Hoc Positioning System(APS)Using AOA[D].DATAMAN Lab Rutgers University,2003.

[4]邱扬刚,张亚,李世中.五元空间阵声被动定位算法及性能研究[J].四川兵工学报,2010,31(2):122-125.QIU Yanggang,ZHANG Ya,LI Shizhong.Acoustic passive localization algorithm based on a five-element spacial matrix and its performance aanalysis[J].Sichuan Ordnance Journal,2010,31(2):122-125.

[5]聂伟荣.多传感器探测与控制网络技术——地面运动目标震动信号探测与识别[D].南京:南京理工大学,2001.