管涌动态发展模型中的非线性渗流研究

2010-08-15罗德兵

湖南水利水电 2010年2期

罗德兵

（澧县澧阳大垸水利管理委员会常德市 415500）

汛期洪水对土石坝特别是双层地基的江河大堤威胁最大的是管涌[1]。管涌一般都是非线性渗流，线性问题只是非线性问题的特例，且适用条件极其有限。在多孔介质的渗流中，达西定律是最基本的本构关系，达西定律的表达式为：V=-KJ。式中K称为渗透系数或水力传导系数。通常，对于固定不变的介质与性质不变的流体，K值不再发生，则称线性渗流。在恒定水头的作用下，管涌的形成与发展是一个动态的发展过程，不但渗透系数在不断地变化，水力梯度也随着多孔介质性质的变化而变化。因此，管涌是非线性渗流的一种，柴军瑞[2]将其划分为流态非线性问题。管涌动态发展的过程不仅仅存在流态非线性问题，还存在多重非线性问题的耦合作用。

1 基本概念

对多孔介质与渗流流体的概念与性质，文献[3～4]中有较详细的描述。现主要强调以下几个基本概念，以助于对管涌动态发展模型的理解。

（1）多孔介质的渗透性。

在达西定律中的常数K，通常称为渗透系数。经证明，常数K不仅与多孔介质的性质有关，还与流体的粘滞系数成反比。设流体的粘滞系数为v时，在同一种多孔介质相同的运动状态下，对不同的流体参数k=K/v相同。因此，K又称水力传导系数，k称为多孔介质的物理渗透性[5]。

（2）多孔介质的比面与迂曲度。

比面和迂曲度是刻画在多孔介质运动流体与介质发生作用频数的重要参数[6]。比面为单位体积多孔介质内孔隙的表面积，记为Σ。迂曲度为流体的路径长度与样品长度之比的平方，即为流体路径长度与其位移矢量模长之比的平方，记为τ。

（3）渗透力。

渗透力是流动着的流体对固体介质的作用力，除与渗透水力坡降、流体性质等因素相关外，对单颗粒而言，它是与颗粒表面积成正比的，可以认为是面力。但对多孔介质而言，它与介质的总表面积成正比，而总表面积是对比表面积进行体积积分，与介质的体积成正比，因此，可以认为它是体力。

2 管涌发展中的非线性渗流问题

对管涌动态发展模型渗流的非线性作用，主要有以下几种因素：

（1）渗流流体性质的非线性变化。

管涌发生后，流体由原来的纯水变化为包含部分固体颗粒的混合流体，这种流体的粘滞系数也会随之变化。而且，由于固体颗粒与水体之间存在相对运动，粘滞系数的变化也变成非线性作用。

（2）渗流空间的非线性变化。

在管涌发生的过程中，由于固体颗粒在多孔介质中存在起动与止动的情况，即流体对固体颗粒存在“搬运”作用。因此，分别对于流体与固体来说，其连续性方程存在非线性迭代问题。当静止颗粒起动时，孔隙比增加，土体内含水量也相应增加，起动的固体颗粒又占据了运动着的流体中的部分体积。当运动颗粒被其他颗粒吸附静止时，孔隙比减少，土体内含水量也相应减小。

（3）固体介质渗透系数的非线性变化。

渗流空间的非线性变化带来的另一个问题是固体介质渗透系数的非线性变化。固体颗粒的起动与止动过程都会改变多孔介质的固体颗粒与孔隙之间的关系，使固体介质的物理渗透性发生了变化。

（4）本构关系的非线性变化。

达西定律的理论推导的前提条件是渗流流体的运动状态为层流状态，流体在层流状态下要使其渗透作用力达到颗粒的起动作用力的可能性是比较小的。因此根据基于管流状态的尼古拉兹实验可知，当流体流速达到某一数值后，其沿程阻力不再与趋向于与流体流速的平方成正比。由此，修正的紊流状态下的达西公式也不再是线性关系。

3 渗流流体性质的非线性变化

混有固体颗粒的流体性质的变化规律，可按混溶型流体与非混溶型流体两种方法进行探讨。

3.1 混溶型流体

渗流流体性质的非线性变体主要是指对混溶有固体颗粒的流体，其性质的变化主要表现为粘滞系数和流体密度的变化。

3.1.1 混溶型流体的假设

混溶性流体的粘滞系数变化理论主要来源于目前的泥沙研究。爱因斯坦[7]、钱宁、万兆惠[8]、沙玉清[9]等对混溶性流体的性质做了研究。采用这种方式进行计算与分析有如下的假设条件：

（1）把流体做为一种混合流体来看待，即在流体运动的过程中，固体颗粒是完全溶在流体里的，它们之间没有相对的运动。

（2）流体与固体介质之间存在固体颗粒的物质交换。流体与固体之间发生物质交换后，它们相应的性质发生了变化。

3.1.2 流体粘滞系数

针对流体性质随固体颗粒含量的变化而变化的规律，存在以下两类描述：

（1）粘滞系数的线性变化。

爱因斯坦总结水体粘滞系数与体积含沙量之间有如下的关系：

当考虑这种流体也是对简单非线性问题的理想化与线性化。它只适用于固体颗粒含量较少的情况。粘滞系数与流体体积含沙量之间的线性关系并不能说明渗流形态的线性关系。

（2）粘滞系数的非线性变化。

目前已有大量学者根据实验总结出粘滞系数的非线性变化规律。包括二次多项式、指数形式等。

3.1.3 流体密度

混溶性流体密度表达式：

式中 ρ0、ρ——纯流体与混合流体的密度；

γs——固体颗粒浮容重；

Sr——混合流体中颗粒的体积饱和度。

3.2 非混溶型流体—基于颗粒流理论

颗粒流最先由Cundall P A,Strack O D L[10,11]等提出。周健[12～14]、曾远[15]、张刚[16]等对其进行了总结，将其应用于管涌的运动状态中。其基本点是分别对纯净流体与固体颗粒进行考虑时的非线性变化规律研究。流体按纯流体考虑，对溶入流体在颗粒分别进行受力分析，并对所有颗粒作用的总和进行积分求和，然后将作用反过来施加给流体。该过程本身就是一个复杂的非线性作用的过程。

3.2.1 颗粒流的基本理论

颗粒流考虑颗粒之间的相互碰撞及固体颗粒与流体之间的相互作用。并基于牛顿第二运动定律、力一位移定律(广义胡克定律)及牛顿流体的本构关系建立固固、固流相互耦合的本构关系。

3.2.2 颗粒流基本的方法与假设

基本假设包括：

（1）颗粒单元为刚性体；

（2）接触发生在很小的范围内，即点接触；

（4）接触处的特殊的接触强度；

（5）颗粒单元为圆形。

接触过程满足如下假设：线性弹簧或Hertz-Mindlin法则；库仑滑块；可选择的连接类型,如一种是点接触；另一种是用平行的弹簧连接,这种平行的弹簧连接可以抵抗弯曲。

它们的作用力都会反作用于运动着的纯流体上。对自由运动颗粒的作用可以看成是作用在流体内部的体积力，将滚动颗粒与滑动颗粒的作用看成是流体表面的面积摩擦力。

3.2.3 固相的运动方程

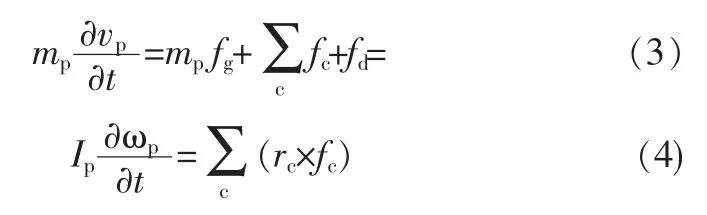
式中vp——颗粒速度矢量；

近年来，数字货币发展迅猛，带来了一系列的投资机会，收益丰厚，但也带来很大的金融风险，尤其是对比特币的炒作，引发了金融市场尤其是数字货币市场的恐慌。世界各国都在完善对数字货币的监管，数字货币将来也有可能代替流通的纸币，发挥货币的职能，但这将是一个漫长的过程，需要世界各国共同加强对数字货币的研发和监管，防止以此引发金融危机。

ωp——颗粒转动速度矢量；

mp——颗粒的质量；

Ip——颗粒的转动惯量；

fg——重力加速度矢量；

fc——接触c（c=1，2，）处颗粒之间的接触力；

rc——接触c处指向颗粒形心的方向矢量；

fd——流体施加于颗粒p的拖曳力，包括浮力与液一固之间的相互作用力。

3.2.4 液相的运动方程

流体运动的纳维—斯托克斯公式中，将流体速度的随体导数按时间与空间分别求导，考虑流体的粘滞系数有可能发生变化，因此，速度的拉普拉斯算子按剪应力张量的变化率代替，并增加流体与固体结构的相互作用，即得到下式：

式中n=n（x，t）——孔隙率；

（x，t）——空间和时间的坐标；

vf=vf（x，t）——平均流体速度矢量；

△p——压力梯度；

τ——平均流体应力张量；

fg——重力加速度矢量；

fint——液一固之间的相互作用力矢量。

4 渗流空间的非线性变化

渗流空间变化的非线性主要指泥沙起动与止动时流体运动的空间发生了变化。

4.1 泥沙颗粒的起动

4.1.1 前期学者的理论成果

对于单个颗粒的临界起动条件，太沙基[17]、扎马林、沙金煊[18]、毛昶熙[19～21]、刘杰[5]、丁留谦[22]等都取得了大量成果。他们总结了大量临界水力坡度的公式，其中大部分都是从竖直向上的方向考虑管涌的形成。

4.1.2 建议的统一公式

考虑自由颗粒管涌发生在任何可能方向，形成管涌的泥沙起动前的围压力随时间成指数变化，并考虑颗粒间的相互粘滞力时，按临界平衡推导出下式：

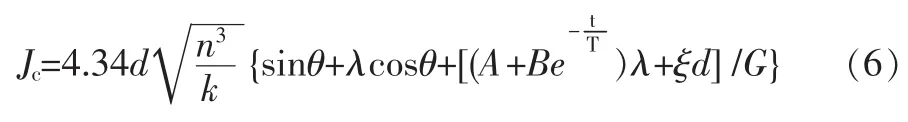
式中Jc——某个颗粒的临界水力坡降；

d——其等效粒径；

n——孔隙率；

k——渗透系数；

θ——管涌方向与水平的夹角；

λ——土体内摩擦系数，可取λ=tanφ；

ξ——颗粒间范德华力的系数[23]。

4.2 泥沙颗粒的止动

在流体中运动的颗粒会因为种种原因有一部分由运动状态变为相对静止，停留在渗流场的某个位置。这不仅减少了流体运动的范围，还增加了固体的体积。因此，它对管涌发展渗流场的影响也是非线性的。

4.2.1 基于颗粒流的碰撞理论

颗粒流最初的模型源于土体的剪切破坏。在土体的剪切破坏中，外加了一个已知运动轨迹的部分做为边界条件，称为墙体。外部对墙体的约束是刚性的，由此墻体不满足运动方程。颗粒流固相的基本运动方程是式（3）、式（4）。

在颗粒流的理论中，每一个颗粒的运动是连续的，颗粒与墙体的碰撞是颗粒静止下来的主要原因。与流体内颗粒与颗粒碰撞相似，颗粒与墙体的碰撞过程也做了相应假设。碰撞的力学特性与颗粒间的碰撞相似。由于墙体表面法向方向一般与颗粒的运动方向会成一定角度，因此，可将其作用力分解为法向方向作用力与水平方向作用力。并在这两个方向对颗粒采用运动方程进行分析，确定碰撞后颗粒的运动状态。

4.2.2 基于随机过程的运动理论

颗粒流中对每一个颗粒都必须采用连续的运动方程，计算量大。对所有颗粒都是球形的假设与实际的颗粒运动状态可能会有一定的偏差。有必要寻找其他的运动模型来弥补其不足。曹敦侣[24]建立了管涌发展过程的随机模型。

在随机过程中，存在大量随机因素影响事物的运动状态，我们需要对这些随机因素进行分类与比较，并确定这些因素的分布形式、对事物运动状态的影响大小等。

首先，需要确定在一个单元体内运动着的固体颗粒的粒径分布与颗粒的运动速度，根据式（6）的起动公式，可以大致估计颗粒的粒径分布，对不同粒径的颗粒需要根据渗流路径与水力梯度估算其流速的分布。

其次，需要估计颗粒的形状与属性，以确定颗粒的运动形式。文献[7]对单个颗粒形状有详细的描述。流体中包含的颗粒运动形式一般可分为自由运动、滑动与滚动等三种形式，小粒径多以自由运动为主，大粒径球形多以滚动为主，块形多以滑动为主。

最后，还需要对多孔介质的某些属性做一些统计与描述。如多孔介质的比面与迂曲度有关。多孔介质的孔隙特性、有可能形成管涌的通道的特性等。

根据以上分析，在一个单元内确定的水力梯度与渗流特性的前提下，可以建立关于颗粒粒径、形状参数与多孔介质特性等参数相关的微分方程式，用来判断颗粒运动过程中与通道发生碰撞次数的概率及静止下来的可能性。然后对各组粒径与各种形式进行累加、积分。求解颗粒静止下来的概率。

5 固体介质物理渗透性的非线性变化

建立固体孔隙特性与物理渗透性之间的关系式。目前已有大量的经验公式，常用的有与d17、d20、d50及孔隙平均孔径相关等多种表达形式。刘杰[4]基于层流状态毛细管管流的推导公式如下：

在管涌的发展过程中，必须考虑孔隙的不均匀性，会使总体的物理导渗性增加。建议根据不同的破坏程度在上式乘以一个大于1的系数。

6 本构关系的非线性变化

流体在层流运动状态下运动时，即不考虑雷诺切应力。颗粒在竖直方向受到的向上的作用力为流体上下速度差引起的压力差。当颗粒密度按计时，不考虑颗粒间的相互粘滞作用时颗粒起动的流体速度平方的临界梯度计算可得：

按此式的判断，竖直方向上层流状态下发生管涌的可能性较小。而现实工程中由于双层地基与土体横观各向同性的影响，管渗多向水平与竖直方向发展，而竖直发展的情况更多。因此，管渗多发生在紊流状态。

（1）层流状态下的渗流的本构关系。

层流状态下的本构关系即为达西定律。

（2）紊流状态下的渗流的本构关系。

尼古拉兹在做管流实验时总结出紊流状态下流体压力梯度与速度的平方成正比。目前，有学者又提出二项式公式、指数公式[25]及与加速度相关等多种公式。

7 管涌动态发展模型的求解思路

上述的几个非线性问题是相互联系与相互作用的。从成因上来说，流体运动的空间发生了非线性的变化，使流体与多孔介质之间存在相互的物质交换。这对流体来说，流体内部纯流体与混溶的固体颗粒之间的相对运动变得更加复杂，从而改变了流体对外表现出的性质：粘滞系数。对多孔介质来说，改变了多孔介质中的孔隙比与孔隙形状，从而改变了多孔介质的物理渗透性。渗流速度与水力坡降之间的非线性关系直接影响着上述一系列非线性相互作用，运动流体的水力梯度是颗粒沿水流方向受力的根本原因，孔隙内流体的速度平方的梯度是颗粒沿水流垂直方向受力的根本原因。流体粘性的变化与固体介质物理渗透性的变化又直接导致了水力传导系数的变化，水力传导系数直接反映不水力梯度与流体速度之间的变化规律。因此，由于上述几个问题之间存在相互耦合作用，管涌动态发展的过程是一个相对复杂的多因素耦合的非线性问题。

解决上述多相渗流的非线性问题，主要有以下几种方法：

（1）混溶性单相渗流——协同无机化学反应。

将溶有固体颗粒的流体看成单一性质的流体进行计算。在计算的过程中，流体与固体之间存在着物质的交换。物质交换的方向（是固体颗粒被流体冲走，溶入固体，还是溶于流体中的固体颗粒沉积下来，形成固体）、物质交换的频繁程度都取决于流体与固体的性质、流体的流速等因素。物质交换的直接后果是导致固体导渗性质与流体性质的变化，从而形成一个简单的耦合运动。

与无机化学反应的反应速度、焓变与熵变等概念相类似，我们可以将物质交换速度看成是化学反应速度，将流体及溶于其中的固体颗粒看成化学反应中的溶液，将多孔介质看成化学反应中的未溶固体，多孔介质的性质与固体的可溶性相类似，流体的水力坡降与渗流速度与化学反应的温度与催化剂相类似。这样，便可建立交换速度的平衡方程。从而模拟管涌现象的发生与发展过程。此交换速度需要做大量的实验后总结归纳出经验公式。与无机化学反应的主要区别是不断有纯渗流流体掺入渗流场，也不断有固体颗粒带出渗流场，即发展方向的不可逆性。

显然，纯流体与固体颗粒不发生相对运动的假设是这种计算方法最大的缺陷。

（2）多相渗流流体间的驱替理论。

目前，石油部门对水、油混合物的多相渗流所采用的方法多为多相渗流流体间的驱替[26～28]。考虑两种互不混溶的流体在同一固体介质中的运动分析方程。其基本原理是基于不同流体混合时浓度差的基质吸力，驱替静止孔隙与流体运动孔隙之间流体相互交换。

采油与管涌的发展模型相比较有三个相同点：

●它们都是由纯水流带动或驱替另一种物体运动；

●它们都具有不均匀的浓度，即存在基质吸力；

●它们都是不可逆过程。

毛细管水油驱替中的基质吸力主要来源于浓度差的压力梯度、界面的表面张力及毛细管吸力等。考虑管涌发展过程中的多相渗流，基质吸力可以看成是总水头相同的流动孔隙与静止孔隙之间的压力差。可将管涌过程中可能运动的固体颗粒（自由颗粒）看成是起动渗透压力较大的Bingham流体。建立无穷维的驱替模型。并用体积含沙量作为刻画流固驱替的程度与标志。

显然，采用这种方法只能近似模拟管涌的动态发展过程。

（3）颗粒流数值解法。

基于颗粒流的基本概念与基本假设的条件下，建立的微分方程。颗粒流的程序已开发出PFC2D与PFC3D等二维、三维程序。周健、张刚[15]等学者将颗粒流在基本概念与管涌形成的机理相结合，提出了管涌的颗粒流发展模型。目前已采用PFC程序做出管涌动态发展模型。

（4）多种非线性渗流的耦合分析方法。

根据以上各种引起非线性的不同因素,建立微元体内：水头—流速—流体与固体的交换—流体内颗粒流的运动及相互作用—固体导渗性质的变化—确定渗流的本构关系—重新计算水头的循环过程。在循环计算的过程中，需要对运动的颗粒按运动状态与颗粒粒径进行统计分析并分类计算，确定起动与沉降的可能性，进而确定固体与流体的物质交换强度。在这方面的无单元法的有限元计算，周晓杰[29]作了初步研究。

（5）管涌动态发展的动力系统分析法。

管涌发展到一定程度（或经处理）后，在出渗区附近形成的通道会调整渗流场的各种参数。下游有可能形成相当于褥垫的排水体，而形成不会发展的无害管涌。这种管涌的发展具有一类稳定的吸引子。即这种管涌的外部荷载在渗流场本身微分算子的收敛区域即谱半径的范围内。

研究管涌动态发展模型的目的管涌发展的稳定性，其次是判断我们所研究的大堤或大坝抵抗管涌变形的时间，即工程抵抗管涌的使用寿命。如果系统不具有整体吸引子，即微分算子在给定水头作用下始终会破坏，那么，我们还需要根据微分算子的发散程度，以时间为计算步，确定系统的发散程度。如果我们能够判断大堤或大坝（或经处理后）在设计荷载作用下其渗透变形具有稳定的吸引子，问题即得到解决。如果不能收敛，我们需要估算系统的使用寿命。

8 结语

管涌的发展过程受多方面非线性因素的影响。求解管涌发展动态过程的模拟也相当复杂。以上几种计算方式各有所长。虽然第一、二种方法存在缺陷，但做了大量简化，计算更方便。采用墙体的形式定义土体中承受土压力的骨架颗粒不是很合适，骨架颗粒与其他堆积在一起处于相对底层的细颗粒之间有可能有相对于颗粒重力大得多的作用力，随着管涌的发展，这些颗粒的起动对骨架的作用可能不仅仅是对墙体（不动体）的作用。颗粒体形也千奇百怪，不可能完全是圆球形，颗粒形状在很大程度上影响了其运动形式，在管涌发展过程中，只有位于大孔径孔隙或临空界面表面的颗粒起动后，其下层的颗粒才有可能起动，因此管涌初期只是个别颗粒的个别运动。等等这些因素都是颗粒流与管涌动态发展过程存在的微小差别，且颗粒流的计算量大，第三种方法也有需要改进的地方。第四种方法计算量大，需要确定的参数与方程多，采用非线性计算程序还很不成熟。第五种方法需要从动力系统与混沌学的角度，将影响管涌发展的各种因素换算成一个复杂的微分算子的作用，然后判断其抵抗外界荷载的谱半径或整体吸引性。应该是一种可能应用于实际的比较理想的方法。

1 中华人民共和国水利部.中国’98大洪水.中国水利年鉴1999[M].北京:中国水利水电出版社,1999.

2 柴军瑞.岩土体水力学非线性问题[J].岩土力学,24(增).2003.159－161.

3 贝尔.李竞生，陈崇希译.多孔介质流体动力学[M].北京:中国建筑工业出版社，1983.

4 薛定谔.王鸿勋，张朝琛，孙书琛译.多孔介质中的渗流物理[M].北京:石油工业出版社,1982.

5 刘杰.土石坝渗流控制理论基础及工程经验教训[M].北京:中国水利水电出版社，2006.

6 孔祥言.高等渗流力学[M].北京:中国科学技术大学出版社，1999.

7 爱因斯坦.钱宁译.明渠水流的挟沙能力[M].北京:水利出版社，1956.

8 钱宁，万兆惠.泥沙运动力学[M].北京:科学出版社，1983.

9 沙玉清.泥沙运动学引论[M].北京:中国工业出版社，1965.

10 Cundall P A,Strack O D L.Particle flow code in 2 Dimensions[A].Itasca Consulting Group,Inc.,1999.

11 Cundall P A,Strack O D L.A discrete numerical model fgraunlar assemblies[J].Geotechnique,1979,29(1):47-65.

12 周健，池永.土的工程力学性质的颗粒流模拟[J].固体力学.2004,25(4):377-382.