反比例函数在实际问题中的应用
2010-08-14安徽省利辛县教育局
✿安徽省利辛县教育局 夏 飞
【重点分析】
本节内容是利用反比例函数来解决生活中的实际问题,其关键是从实际问题中抽象出函数关系,从而将文字转化为数学语言,通过反比例函数的概念列出函数关系式,再利用反比例函数的性质、思想方法去解决实际问题.
利用反比例函数解决实际问题的关键是:建立反比例函数模型,列出反映实际问题的反比例函数解析式:
(1)列出反映实际问题中的函数关系式首先应分析清楚各变量之间应满足的分式,即:实际问题中的变量之间的关系→建立反比例函数模型→解决实际问题.
(2)在列反映实际问题的函数关系式时,一定要在列出的关系式后面注明自变量的取值范围.
【学法指津】
1.学会把实际问题转化为数学问题,充分体现数学知识来源于实际生活又服务于实际生活这一原理.
2.要熟悉一些常见的函数模型,能用函数的观点分析、解决实际问题,让实际问题中的量的关系在数学模型中相互联系,并得到解决.
3.要认真阅读题目,理解题意,抓住关键量,主要是题目中的定值、常量和恒定不变的数据等,准确地抽象出函数关系,然后正确设出函数关系式,用待定系数法求出待定系数.
4.由于实际问题中有很多限制条件,因此当自己认为解决了问题后,还要回头再把题目看一看,是否有疏忽的地方,以免求出的答案不符合题意.
【典例解析】
例1:如下图,市煤气公司要在地下修建一个容积为104m3的圆柱形煤气储存室.

(1)储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系?
(2)公司决定把储存室的底面积S定为500m2,施工队施工时应该向下掘进多深?
(3)当施工队按(2)中的计划掘进到地下15m时,碰上了坚硬的岩石,为了节约建设资金,储存室的底面积应改为多少才能满足需要(保留两位小数)?
分析:(1)根据圆柱体的体积公式,我们有S×d=104,变形可得
(2)把S=500代入所求得的解析式,即可求得深度d;
(3)把d=15代入解析式,即可求得储存室的底面积S.
答:如果把储存室的底面积定为500m2,施工时应向地下掘进20m深.
答:当储存室的深为15m时,储存室的底面积应改为666.67m2才能满足需要.
例2:某地上年度电价为0.8元,年用电量为1亿度,本年度计划将电价调至0.55~0.75元之间,经测算,若电价调至x元,则本年度新增用电量y亿度与(x-0.4)元成反比例,又当x=0.65时,y=0.8;
(1)求y与x之间的函数关系式;
(2)若每度电成本价为0.3元,则电价调至多少元时,本年度电力部分收益将比上年度增加20%?[收益=用电量×(实际电价-成本价).]
分析:(1)此题属于把实际问题转化为求反比例函数的解析式的问题.
(2)此题属于函数解析式的应用问题.要解决的问题是:若每度电成本价为0.3元,本年度电力部分收益将比上年度增加20%?须考虑“收益=用电量×(实际电价-成本价)”这一关系.而上年度电价为0.8元,年用电量为1亿度.于是可算出本年度电力部分收益为0.6亿元.
解:(1)由于本年度新增用电量y亿度与(x-0.4)元成反比例,所以可设所求的关系式为,又当x=0.65时,y=0.8;代入,可求得k=0.2,
解得:x1=0.5,x2=0.6;根据实际问题,这两个值都符合题意.
答:电价调至0.5或0.6元时,本年度电力部分收益将比上年度增加20%.
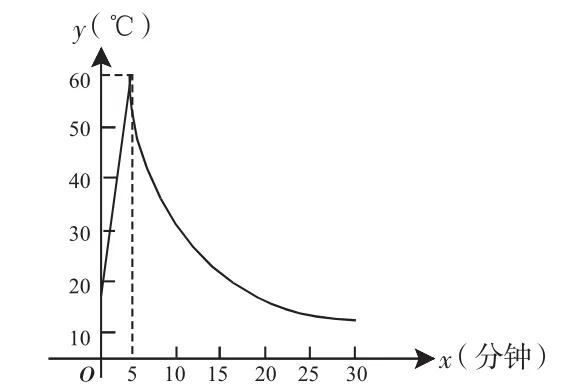
例3:制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与x时间成一次函数关系;停止加热进行操作时,温度y与x时间成反比例关系(如下图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
分析:本题主要考查一次函数、反比例函数解析式的求法.但由于本题是由一次函数和反比例函数组成的分段函数,所有要注意分类讨论,分别写出函数关系式.(1)显然将材料加热时,即0≤x≤5,y与x是一次函数,直线过点(0,15),(5,60);停止加热时,即 x≥5,y与 x是反比例函数,图像过点(5,60),易求得函数关系式;(2)当材料的温度低于15℃时,需停止操作,即令y=15,求对应的自变量的值.
解:(1)将材料加热时,y与x是一次函数关系,可设y=kx+b(0≤x≤5).
∵当x=0时,y=15;当x=5时,y=60;
∴当0≤x≤5时,y与x的关系式为:y=9x+15.
∴x=20.即从开始加热到停止操作,共经历了20min.
分析:综合运用一次函数和反比例函数的知识解题,一般要先根据题意画出图像,然后可借助图像和题目中提供的信息解题.
(2)解法一:
y=-x+2,当 y=0 时,x=2,M(2,0).
∴OM=2.作AC⊥x轴于C,作BD⊥x轴于D.

解法二:
y=-x+2,当 时 x=0 时,y=2,N(0,2).∴ON=2 .
作AC⊥y轴于C,BD⊥y轴于D.



【总结反思】
用函数观点处理实际问题,关键在于分析实际情境,建立函数模型,并进一步明确数学问题,将实际问题置于已有的知识背景之中,用数学知识重新解释这是什么?可以看到什么?逐步形成解决实际问题的能力.而在解决问题时不仅要充分利用函数的图像,渗透数形结合的思想,还要注意函数不等式、方程之间的联系,以及学科之间知识渗透.重要的有以下几点经验:
1.通过分析,把实际问题中的数量关系转化为数学问题中的数量关系;利用构建好的数学模型、函数思想来解决这类问题.
2.通过观察图像,把图像中提供、展现的信息转化为与函数有关的知识来解题.
3.综合运用一次函数和反比例函数求解两种函数解析式,往往仍用待定系数法.
【典题演练】(供教师做习题参考.)
1.已知某矩形的面积为20cm2.
(1)写出其长y与x宽之间的函数表达式;
(2)当矩形的长为12cm时,求宽为多少?当矩形的宽为4cm时,其长为多少?
(3)如果要求矩形的长不小于8cm,其宽最多应是多少?
2.某蓄水池的排水管每时排水8m3,6h可将满池水全部排空.
(1)蓄水池的容积是多少?
(2)如果增加排水管,使每时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化?
(3)写出t与Q之间的函数关系式;
(1)分别写出这两个函数的表达式.
(2)你能求出点B的坐标吗?你是怎样求的?
(3)若点C坐标是(-4,0),请求△BOC的面积.

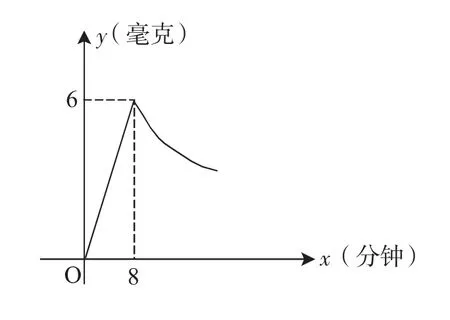
4.为了预防流行性感冒,某学校对教室采用药熏消毒法进行消毒.已知,药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后,y与x成反比例(如下图所示).现测得药物8分钟燃尽,此室内空气中每立方米的含药量为6毫克,请你根据题中所提供的信息,解答下列问题:
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过_______分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
答案与提示:
2.(1)蓄水池的容积为:8×6=48(m3).(2)答:此时所需时间t(h)将减少.(3)t与Q之间的函数关系式为:
3.(1)正比例函数表达式为:y=2x;反比例函数表达式为2)①可利用图像,根据对称性来求;②可将y=2x与组成方程组,求出方程组的解.答案:B的坐标为.(3)由于点C坐标是(-4,0),B的纵坐标为,所以△BOC的底边长为4,高为,则(面积单位).
