多加性QoS约束下的链路分离路由算法

熊轲，裘正定，张煜，张宏科

（1. 北京交通大学 计算机与信息技术学院，北京 100044；2. 清华大学 电子工程系，北京 100084；3. 北京交通大学 电子信息工程学院，北京 100044）

1 引言

网络多媒体业务和实时性业务的飞速增涨，迫切要求网络为其提供相应的QoS保障。与此同时，光交换技术和传输技术的发展使得网络的传输速率成倍增长，在高速网络中即使很短暂的链路失效，也会造成数据包的大量丢失和网络QoS的急剧下降。如何提高网络可靠性和QoS恢复能力已成为网络研究的重要课题[1～3]。

在通信的源和目的节点间寻找满足QoS约束的2条分离路径，一条作为主用，另一条作为备用。在主用路径失效时，将业务流迅速切换至备用路径传输，被认为是可同时提高网络可靠性和QoS保障的重要方法[1,2,4～8]。多约束分离路径亦十分有利于网络流量工程、负载均衡和拥塞避免的实施。

通常QoS约束可分为链路约束和路径约束2类。链路约束是对单条链路的约束，如带宽约束，属于凹性约束；路径约束则指对传输路径上所有链路QoS参数端到端总和的约束，如花费(cost)、延时(delay)等约束，属于加性约束。链路约束处理起来相对简单，只需在路径计算前将不满足约束条件的链路删去即可[8]。路径约束则需要将路径上端到端的参数叠加起来考虑，因此要复杂的多。当路径约束个数大于2时，路由问题就变NP问题[9]。分离路径包括链路分离和节点分离2类。前者要求路径间无共用链路，后者要求路径间无共用节点。节点分离一定为链路分离，反之则不成立。因此讨论链路分离路径是研究分离路径问题的基础。

本文主要研究多个加性QoS约束下的链路分离路径算法，旨在在一对通信的源和目的节点间寻找2条链路分离且满足多个加性QoS约束的路径，并提出了与网络结构无关的多约束链路分离路径路由算法(MCLPRA, multiple constrained link- disjoint path routing algorithm)，该算法基于多约束下的最短路径精确算法(SAMCRA)[9,10]，在解的搜索过程中，首先对解空间按照解的不同构成形式进行分类，然后按类进行搜索处理；引入了控制搜索精度和深度的控制参数，能够保证对任意结构网络求得可行解。

2 问题描述及研究现状

将网络抽象为加权有向图，记为G( V, E)。网络中的路由设备和通信链路分别用图中的节点和有向边表示。V代表G中节点的集合，E代表G中有向边的集合，(u, v)表示从节点u到节点v的一条有向边。G中每条边都带有m维的加性权重向量W( u, v)=[w1( u, v), w2( u, v),…,wm(u, v)]。用s和t分别代表通信的源和目的节点，P为从s到t的一条路径，wi( P)表示P的第i维权重，路径P的权向量W( P)=[w1( P), w2( P),…,wm(P)]，其中

用E( P)={(u, v)|(u, v)∈P}代表路径P上的边的集合，用V( P)代表路径P上的节点集合，V( P)={u|＜u, v＞∈P或＜v, u＞∈P}。

定义1 非线性长度。给定带m维权重的加权有向图G(V, E)和m维约束向量C，C=[c1, c2,…,cm]，G中路径P的非线性长度定义为[9,10]

非线性长度是归一化的长度。当l( P)＞1.0时，路径P至少有一维权重超出了约束C。

定义2 链路分离路径(link-disjoint path)假设P1和P2为G( V, E)中的2条路径，若E( P1)∩E( P2)=∅，则P1与P2为链路分离路径。

定义3 多约束链路分离路径对(MCLPP, multiple constrained link-disjoint path pair)问题。给定一个加权有向图G( V, E)和一个m维的约束向量C=[c1, c2,…,cm]，m≥2。MCLPP问题的目的是在源s和目的t节点之间找到2条路径P1与P2，要求E( P1)∩E( P2)=∅，且P1与P2均满足约束C，即wi( P1)≤ci, wi( P2)≤ci，1≤i≤m。

实际上，在s和t间可能同时存在多条满足约束C的链路分离路径对，往往希望找到路径总长最小的一对。当l( P1)+l( P2)为最小时，定义{P1, P2}为MCLPP的最优解。

近年来，多QoS约束链路分离路由问题受到了研究者的广泛关注，然而新的研究基本都是针对delay单个约束的，旨在找出一对链路分离路径，在满足delay约束的前提下达到2条路径总的cost最小。当给定的delay约束针对的是路径对中的每条路径的延时时，问题被称为DCLDOP-I，当delay约束针对的是路径对中2条路径延时的总和时，问题被称为DCLDOP-II。文献[13]对DCLDOP-I和DCLDOP-II问题进行了建模，证明了这2种问题都属于NP完全问题。文献[14]提出了针对这2种问题的近似求解算法。文献[15]对DCLDOP-II问题进行了研究，提出了单条链路失效下的路径恢复算法。文献[16]研究了Min-Min问题，旨在求解2条满足QoS约束的分离路径，且实现较短的路径cost最小。文献[17]采用了将 2个加性权值进行线性组合的方法来求解满足QoS约束的分离路径，并给出了求解算法，所提算法虽然简单，却不能保证一定能求得可行解。

MCLPP问题由文献[11,12]提出并证明了MCLPP为NP完全问题，分析了多约束链路分离路径问题与单约束链路分离路径问题的不同，且给出了启发式求解算法 DIMCRA。本文在文献[11,12]的基础上，对MCLPP进行了进一步的研究，旨在通信的源和目的节点间找到一对链路分离路径，且每条路径都满足2个或2个以上的QoS约束。

目前求解 MCLPP问题的最直观的算法为 RF算法。其原理是：先计算一条满足QoS约束的最短路径，然后删去该路径上的所有链路的修正图，再在修正图中解得另一条最短路径。RF算法能保证所求得的2条路径为链路分离路径，但由于在求解过程中删去了第一条路径上的链路，破坏了原网络的连通性，导致很多情况下得不到最优解，甚至连可行解也得不到。

DIMCRA[10,11]算法由单约束的链路分离路径算法LBA[10,11]演化而来，对RF算法有一定的改进。给定G( V, E)和约束C，其步骤如下。第 1步：执行SAMCRA，寻找1条最短路径1P；第2步：将1P的所有链路反向并置其权重为 0，得修正图G′( V, E )；第3步：在 G ′( V, E )中执行SAMCRA，寻找1条满足约束2C的最短路径 P2，若 P2不存在，算法停止；第4步：取 P1和 P2的并集，删去反向链路出现在 P1上的 P2的链路和反向链路出现在 P2上的 P1的链路，将余下的链路组成2条路径 { P1′, P2′} ；第 5步：检查集合 { P1′, P2′}中的每条路径，若路径Pi′(i=1,2)不满足约束，则从修正图 G ′( V, E )中删去 Pi′与 P1未发生交叠的链路集合，得到更新的修正图 G ′′( V, E )，返回第3步；否则，算法停止。

与RF一样，DIMCRA也能保证所求解一定满足链路分离，但由于在解搜索过程中采用了删除不满足约束条件的路径上的部分或全部链路的方法，见算法第 5步，亦破坏了网络的连通性。因此DIMCRA同样不能保证对任意结构的网络都可求得可行解和最优解，如本文第5节的算例3和算例5。

3 MCLPRA

针对上述问题，本文提出了 MCLPRA。与DIMCRA算法相似，MCLPRA也以SAMCRA为基础，充分利用了SAMCRA的几个特点：①基于非线性长度；②k-shortest path特性，即在求解最短路径的搜索过程中，不仅可以得到最短路径，也可以得到第2短路径，……，第k短路径；③多约束路由最短路径的无环路精确算法。

MCLPRA采用先将解空间分类，然后按类进行搜索处理的方法。在算法处理过程中，保持了原网络的结构和连通性，确保了解空间的完整性，引入了搜索深度控制参数，能够保障对任意网络求得可行解。需要补充说明的是，DIMCRA的第3步仅求得了最短的一条2P，而MCLPRA利用了SAMCRA的k-shortest path特性，对SAMCRA进行了修改，使其在一次运行过程中可将满足约束的所有2P路径记录下来，然后将这些路径按类处理，进行解的搜索。

3.1 MCLPRA的求解步骤

下面给出 MCLPRA的求解步骤，给定加权有向图G( V, E)和约束向量C。

第1步：执行SAMCRA，求1条最短路径1P；

第2步：将1P的所有链路反向并置其权重为0，得修正图 G ′( V, E )；

第3步：在修正图 G ′( V, E )中运行SAMCRA，计算出从s到t的满足约束向量2C的k条最短路径集合 S = { P1′ , … ,Pk′}，如果S为空，算法停止；

第4步：将S按如下规则分成2个子集：

下面给出Search_Sβ(P1, Sβ,T)的处理过程，其中T为搜索深度控制参数。

接下来介绍Search_in_Linkjoint(Pa, Pb)的步骤。功能是从有共用链路的2条路径Pa, Pb的链路所构成的集合中搜索满足约束的可行解。

第1步：取Pa和Pb的并集，从中删去反向链路出现在Pa上的Pb链路和反向链路出现在Pb上的Pa上的链路，将余下的链路组成2条路径{Px, Pw};

第2步：

if V( Px)∩{V( Pw)-s-t}=V( E( Px)∩E( Pw))≠∅

最后介绍Search_in_nodeshared(Pa, Pb)的步骤。功能是从有共用节点的2条链路分离路径Pa, Pb所构成的链路集合中，找到满足约束C且长度和最小的2条链路分离路径。

第1步：取Pa和Pb的并集，由Pa和Pb的链路构成一个G( V, E)的子图Gsub；

第2步：对Gsub做如图1所示的等效变换，在等效图中找到由Gsub链路构成的2条满足约束的链路分离路径{,}，且l()+l()为最小。

对图1(a)的结构，通过合并出度与入度都为1的节点相连接的链路，可得到等效图1(b)，在图1(b)的结构中易找到s和t之间的非线性长度和最小的链路分离路径对，图1(b)中为{sabt, sbcdt}。

3.2 MCLPRA的求解过程

下面通过算例说明MCLPRA的求解过程。

图1 等效变换

算例1 如图2(a)所示网络，C=(10,10)。目的是在源节点s和目的节点t间寻找一对满足C约束条件的链路分离路径。第1步在图2(a)上运行SAMCRA得到最短路径P1为sabt。第2步如图2(b)所示，将sabt上的链路反向，并且重置链路权重为0。第3步在图2(b)上运行SAMCRA，求得满足2C约束的路径集合S={sdt, sbat}。第4步对S进行分类，sbat∈Sβ，sdt∈Sα。第5步先查找Sα中的最短路径，Sα中只有一条路径sdt，故Pα=sdt。然后调用Search_Sβ()搜索Sβ构成的可行解中的最优解。取Sβ中的最短路径sbat，由于sbat与1P有共用链路，所以调用Search_in_Linkjoint()处理，从sabt和sbat链路构成的并集中去掉共用链路ab，剩余链路构成2条链路分离路径{sat, sbt}，经判断sat与sbt均满足约束C，故{sat, sbt}为Sβ与1P构成的最优解。因为P1和sdt均满足约束C且l( sat)+l( sbt)＜l( sabt)+l( sdt)，故{sat, sbt}为最终解。显然，该解为图2(a)上的最优解。

图2 MCLPRA算例1

算例2 如图3(a)所示网络，C=(10,10)。MCLPRA第1步是在图3(a)上运行SAMCRA得到最短路径1P为sabct。第2步如图3(b)所示，将sabct上的链路反向，重置链路权重为0。第3步在图3(b)上运行SAMCRA，求得满足2C约束的路径集合S，求解结果只有一条路径sbt满足要求。第4步对S进行分类，sbt属于Sβ，Sα为空。第5步搜索Sβ，调用Search_in_Linkjoint( )的过程，因为sbt与1P无共用链路，所以调用Search_in_nodeshared( )。在由1P和sbt链路构成的并集中，除了{sabct, sbt}这组链路分离的路径，还有一组为{sabt, sbct}。由于路径sbt的权向量为(11,2)，不满足约束条件(10,10)，故{sabct, sbt}不能作为MCLPRA的解。经判断，sabt和sbct均满足约束条件，故在算例2中，MCLPRA的解为{sabt, sbct}，该解也是图3(a)上的最优解。

图3 MCLPRA算例2

4 MCLPRA特性分析

本节将从理论上分析MCLPRA设计的科学性，从MCLPP解的构成形式入手证明MCLPRA求解结果与网络结构无关，在此基础上给出MCLPRA求得可行解和最优解的控制参数T的取值。

定理1 给定加权有向图G( V, E)，1P为节点s和t间非线性长度最短路径，若s和t间满足约束向量C(dim(C)≥2)的MCLPP问题的最优解{P1*,P2*}存在，则{E( P1*)∪E( P2*)}∩E( P1)≠∅成立。

证明 假设{E( P1*)∪E( P2*)}∩E( P1)=∅，则有E( P1*)∩E( P1)=∅且E( P2*)∩E( P1)=∅。因为P1*和P2*链路分离，故E( P1*)∪E( P2*)=∅。因此，P1*、P2*和P1为链路彼此分离的3条路径。又因为P1为s和t间的最短路径，可得

这与定理1题设{P1*,P2*}为最优解矛盾，故假设不成立。定理1得证。

推论1 给定加权有向图G( V, E)，P1为节点s和t间非线性长度最短路径，若s和t间满足约束向量C(dim(C)≥2)的MCLPP问题的最优解{P1*,P2*}存在，当且仅当E( P1*)∩E( P1)=∅时，P1=P2*(P1*和P2*互换推论1仍然成立)。

证明 由定理1{E( P1*)∪E( P2*)}∩E( P1)≠∅，所以有E( P1*)∩E( P1)≠∅或E( P2*)∩E( P1)≠∅。假设E( P1*)∩E( P1)=∅，若P2*≠P1，最优链路分离路径对则为{P1, P1*}，这与推论1题设矛盾，假设不成立，必要性得证。若P2*=P1，因和P2*为链路P1*分离路径对，E( P1*)∩E( P1)=∅，充分性得证。故推论1成立。

定理1和推论1说明了对于任意结构的网络，如果MCLPP的最优链路分离路径对{P1*,P2*}存在，最短路径要么与P1*和P2*都相交，要么和其中的一条重合。故给定加权有向图G( V, E)，P1为从源、目的间的最短路径。S={P1′,…,Pk′}为MCLPRA第3步求得结果。∀P2∈{P1′,…,Pk′}，P1与P2的结构关系只能为下列4种情况之一。

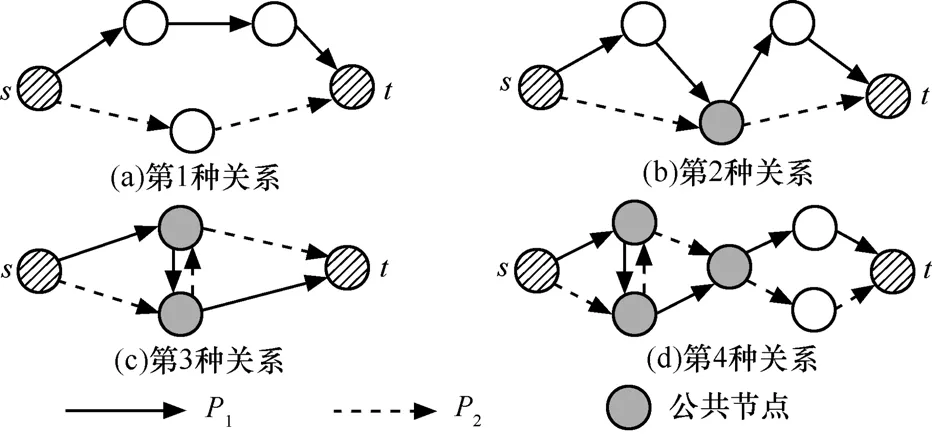
图4 P1与P2路径的4种关系

① E( P1)∩E( P2)=∅ 且V( P1)∩{V( P2)-s-t}=∅，如图4(a)所示，P1与P2既无共用节点，也无共用链路；

② E( P1)∩E( P2)=∅,V( P1)∩{V( P2)-s-t}≠∅，如图4(b)所示，P1与P2有共用节点，但无共用链路；

③ E( P1)∩E( P2)≠∅, V( P1)∩{V( P2)-s-t}≠∅且V( P1)∩{V( P2)-s-t}=V( E( P1)∩E( P2))，如图4(c)所示，P1与P2既有共用节点，也有共用链路，但所有共用节点都和共用链路关联；

④ E( P1)∩E( P2)≠∅ ，V( P1)∩{V( P2)-s-t}≠∅且V( P1)∩{V( P2)-s-t}≠V( E( P1)∩E( P2))，如图4(d)所示，P1与P2既有共用节点也有共用链路，但并非所有共用节点都与共用链路关联；

在上述表达式中，E( P1)∩E( P2)表示P1与P2共用的链路的集合，V( E( P1)∩E( P2))表示P1与P2所有共用链路上的节点的集合；

∀P2∈{P1′,…,Pk′}，若P1和P2属于第①种关系，则{P1′,…,Pk′}中的最短路径min{P1′,…,Pk′}和P1构成的链路分离路径对即为总长最短的链路分离的路径对，如果P1和min{P1′,…,Pk′ }均满足约束，则{P1,min{P1′,…,Pk′ }}为最优解；若P1和P2属于第②种关系，P1和P2可构成多组链路分离路径对（如图4(b)的结构中存在2组链路分离路径对），处理方法是从满足约束的路径对中选取总长度最小的一组作为最优解，具体过程见Search_in_nodeshared()的处理过程；若P1和P2属于第③种关系，可先将P1和P2共用的链路去除，将其转换成情况①进行处理；若P1和P2属于第④种关系，可先将P1和P2共用的链路删除，将其转换成情况②进行处理；对情况③和④的详细处理过程见第2节的Search_in_ Linkjoint( )。

在给定的任意网络中，由MCLPRA第3步求得的集合S={P1′,…,Pk′}上的路径P2与P1的关系必然属于上述4种关系中的一种。MCLPRA第4步先对S上的路径按照与P1的结构关系进行分类，再针对不同情况分别进行处理，最后比较选取各种情况下的最优解作为最终求解结果，以此来保证寻求所得可行解中的最优解。定理1、推论1以及MCLPP解构成的4种可能情况表明了本文所提算法MCLPRA采用先计算最短路径P1，再求{P1′,…,Pk′}，然后按类处理求解过程的科学性。MCLPRA在求解过程中未对原网络拓扑进行改变，保持了网络的连通性和解空间的完整性，故求解结果与网络的结构无关。

由MCLPRA求解步骤可以看出，在Search_Sβ()操作中引入了参数T来控制搜索的精度和深度，本文将T设置为减计数器来控制搜索循环的次数。

证明 MCLPRA第3步采用SAMCRA计算出图中所有满足2C约束的路径集合S={P1′,…,Pk′}。根据定理1、推论1和对解构成的4种情况的分析，MCLPP的最优解一定由P2与P1构成，P2∈S。根据MCLPRA，Sα∪Sβ=S ， Sα为满足情况①的P2的集合，Sβ为情况②、③和④的集合，MCLPRA分别求得Sα上的最优解和Sβ上的最优解，选择其中最优的一组为最终解。对于Sα，Sα中最短的路径Pα与P1组成的分离路径对即为Sα上的最优解。对于Sβ，在Search_Sβ()中参数T可控制搜索Sβ的深度。根据算法过程，在搜索的每一次循环中，Sβ的当前最短路径在处理完后被删除，而T的值也被减1，当Sβ中的路径全被处理完毕时，即可搜索到Sβ上的最优解，当可以保证Sβ上的路径被全部处理，因而时可确保MCLPRA所得最优解不丢失。

推论2 当T取判决条件——在Sβ中搜索到与1P构成满足约束条件的链路分离路径的一组可行解就退出搜索循环时，MCLPRA能够保障对任意结构的网络求得可行解，并且该可行解为当前搜索深度下的可行解中的最优解。

证明 根据前文所述，MCLPRA的可行解落在Sα和Sβ与最短路径1P构成的路径对上。Sα中最短的路径Pα与1P组成的分离路径对即为Sα上的最优解。对于Sβ，如果在Sβ中搜索到与1P构成满足约束条件的链路分离路径的一组可行解就退出搜索。根据算法过程，MCLPRA的最终解为该组可行解与Sα上可行解中最优的一组。推论2得证。

5 MCLPRA与DIMCRA的性能比较

DIMCRA是目前求解 MCLPP问题最有效算法，故对MCLPRA和DIMCRA进行对比分析。

5.1 算例比较

算例3 仍取算例1中的网络和相同的约束，如图5(a)所示。若运行DIMCRA，第1、2步的运行过程和结果与MCLPRA的第1、2步一样（见图5(a)和图5(b)），所得最短路径1P为sabt。第 3步，在图 5(b)上运行SAMCRA，解得最短的路径2P为sdt。第4步，因为1P和2P已经是链路分离路径，转至第5步。经判断，1P和2P均满足约束C，算法结束。所以DIMCRA在图5(a)的网络上的求解结果为{s abt, s dt}。显然{s abt, s d t}仅为图5(a)上的一个可行解，并非最优解，而MCLPRA可以求得最优解(见算例1)。

图5 DIMCRA算例3

算例 4 仍采用图 5(a)的拓扑，将约束向量修改为 C = ( 7,7)。运行 MCLPRA，求解过程与结果仍与算例1相同。若运行DIMCRA，前4步过程和图 5(a)、图 5(b)和图 5(c)相同，可求得1P=sabt，2P=sdt。在第5步中，因为2P的权向量为(7,8)，不满足C的约束，故2P上与1P不相交链路被删除，结果得到图6(a)所示的修正图，并返回第3步，在图6(a)上重新运行SAMCRA求得新的最短路径sbat。第4步将sbat与1P的链路并集中共用链路ab删除，将剩余链路组成2条新的链路分离路径{sat, sbt}。第5步判断{sat, sbt}满足约束为DIMCRA的最终解。

图6 DIMCRA算例4

在算例4中，虽然DIMCRA得到了与MCLPRA相同的解，但运行了3次SAMCRA，而MCLPRA仅运行了2次SAMCRA。

算例5 采用图3(a)所示的拓扑和相同的约束。若运行DIMCRA，前3步与MCLPRA相同，如图3(a)、图 3(b)和图 3(c)所示，可得到1P=sabct，2P=sbt。第4步，因为1P与2P无共用链路，转而执行第5步。由于2P的权向量为(11,2)，不满足C的约束，故2P与1P不相交的链路被删除，结果得图7所示修正图，然后返回第3步。显然，在图7的结构上，已不存在从s到t的路径，算法终止，故此算例中 DIMCRA返回为无解。而算例 2已表明MCLPRA可以在图3(a)的网络上得到最优解。

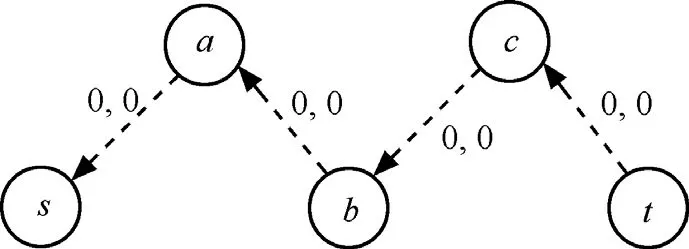
图7 DIMCRA算例5

综上所述，MCLPRA的求解能力要高于DIMCRA。原因在于：① DIMCRA对2P采用了计算出一条就处理一条的方法，一旦满足约束条件就终止算法。这样的过程实际上求得的只是算法最先搜索到的可行解，并未进行最优解的搜索处理，因而DIMCRA不能保证对任意网络求得最优解；② DIMCRA的第5步，对不能和1P构造满足约束条件的分离路径对的2P，采用删链路的处理，破坏了网络的原本结构和连通性，导致了可行解和最优解的丢失，因而也不能保证对任意网络求得可行解；③MCLPRA避免了DIMCRA上述几个问题，是一种与网络结构无关的MCLPP求解算法，这一点第4节已论证。

5.2 仿真比较

本小节通过仿真实验对这2个算法进行比较，仿真采用随机拓扑图(RGU)[18]，RGU图的节点数为N，链路密度ρ取值为0.2。每条链路都带有m维的加性权重, 每维权重均服从[0,1]上的均匀分布。仿真所用计算机CPU主频为1.9GHz，内存为1G。RGU图的节点数取为 100、150、200、250、300、350、400、450和500，每个N上生成1 000个RGU。取 ci=1(1 ≤ i ≤ m )，在m=2和m=3的条件下分别进行实验。每个RGU上运行MCLPRA和DIMCRA各1次。

图8给出了MCLPRA和DIMCRA分别在2约束和3约束下每个N上的1 000个RGU上成功求解的比率。

图8 算法求解成功率比较

由图8可以看出：① MCLPRA的可行解求解概率都高于相同情况下的 DIMCRA。2个算法的求解成功率都随着网络节点数的增加而提高，这是因为ρ一定的情况下，N越大网络连接密度越高，网络可行路径数量也在增长，客观存在可行解的概率就越大。②另外，仿真结果显示MCLPRA的可行解求解率并不总是 100%。这是因为：MCLPRA基于SAMCRA，MCLPRA对任意拓扑均可保证求得可行解的前提条件是在第3步运行SAMCRA时求得并存储所有满足约束的可行解，因为计算机的实际存储能力有限，仿真实验中只选取所有满足2C路径中前20条最短路径进行存储和搜索，因而会有解的损失，要提高求解成功率，可以适当增加T的值；随机生成的RGU很可能客观上并不存在可行解，因而也就难以求解，这也是网络节点数较少时，2种算法求解成功率都偏低的原因之一，即便如此，仿真结果仍表明即使在限制了搜索范围的情况下，MCLPRA的可行解求解平均概率仍要高于DIMCRA。③在2约束条件下，MCLPRA和DIMCRA的平均求解概率都高于3约束的条件，这是因为约束个数越少网络的可行路径数目越多。

图9给出了MCLPRA和DIMCRA分别在2约束和3约束下在每个N上的1 000个RGU上所求分离路径对的平均非线性长度和情况。结果表明，MCLPRA所求解的平均总长度明显小于 DIMCRA所求解的平均总长度，即MCLPRA所求解优于DIMCRA。

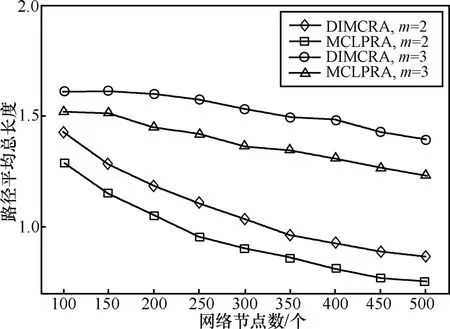
图9 算法所求解的平均长度比较

图10给出了MCLPRA和DIMCRA分别在2约束和3约束下在每个N上的1 000个RGU平均执行时间开销对比结果。结果显示，MCLPRA的时间开销略高于DIMCRA，这是因为要实现算法更高的求解率和更优的求解结果, 往往需要以增加一定的复杂性为代价。从图中可以看出，节点数在500，平均连接度达200的情况下(即高密度连接的复杂网络)，算法的执行时间开销仍在数百毫秒，这对网络的路由计算仍处于可行的范围之内。

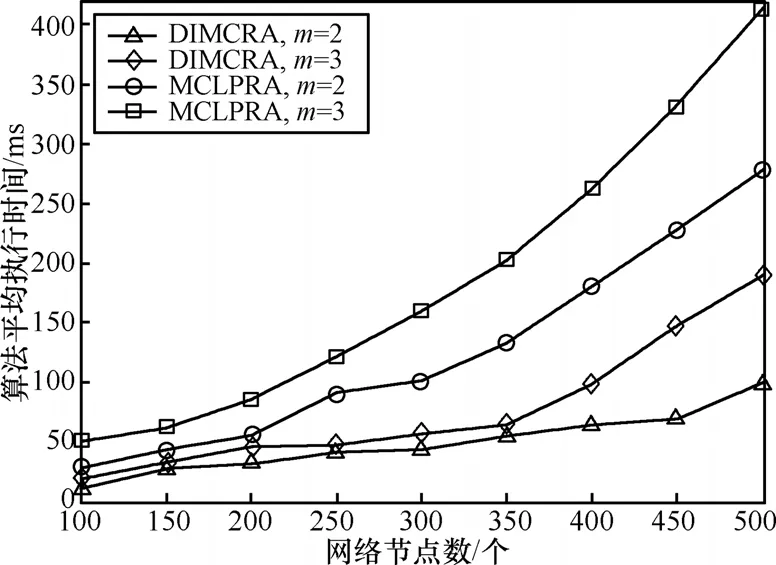
图10 算法所求解的平均长度比较

上述实验说明MCLPRA在可行的执行开销内，求解成功率和所求解都明显优于现有算法。

6 结束语

本文针对多个加性 QoS约束下的链路分离算法进行了研究，提出了基于解空间分类搜索的算法MCLPRA，给出了MCLPRA的求解过程。从理论上分析了 MCLPP问题解的构成形式，证明了MCLPRA对任意结构的网络均可求得最优解，并给出了 MCLPRA求得最优解的控制参数取值条件。通过理论分析和仿真比较，MCLPRA均可获得比DIMCRA更优的求解性能。笔者下一步工作将对MCLPRA进行优化和改进，并进一步降低其算法复杂性。

[1] DAS A, MARTEL C, MUKHERJEE B, et al. A better approach to reliable multi-path provisioning[A]. IEEE Global Communications Conferences (GLOBECOM)[C]. 2007. 2724-2728.

[2] SAWADA N, KANEKO K. Pairwise disjoint paths in pancake graphs[A]. Eighth International Conference on Parallel and Distributed Computing, Applications and Technologies, DPCAT ’07[C]. 2007.376-382.

[3] CHEN S, NAHRSTEDT K. On finding multi-constrained paths[A].IEEE International Conference on Communications ICC’98[C]. 1998.874-879.

[4] TAFT-PLOTKIN N, BELLUR B, OGIER R. Quality-of-service routing using maximally disjoint paths[A]. The 7th International Workshop on Quality-of-Service[C]. 1999. 119-128.

[5] GUO L, LI L M, CAO J, et al. On finding feasible solutions with shared backup resources for surviving double-link failures in path-protected WDM mesh networks[J]. Journal of Lightwave Technology, 2007, 25(1): 287-296.

[6] XIONG K, QIU Z D, ZHANG H K, Towards link-disjoint paths under multiple additive QoS constraints[A]. The 2nd IET International Conference on Wireless Mobile and Multimedia Networks (ICWMMN)[C].2008. 119-127.

[7] XU D H, QUAO C M, XIONG Y Z. Ultrafast potential-backup-cost(PBC)-based shared path protection schemes[J]. Journal of Lightwave Technology, 2007, 25(8): 2251-2259.

[8] VAN MIEGHEM P, DE NEVE H, KUIPERS F. Hop-by-hop quality of service routing[J]. Computer Networks, 2001, 37(3/4): 407-423.

[9] XUE G L, SEN A, ZHANG W Y, et al. Finding a path subject to many additive QoS constraints [J]. IEEE/ACM Transactions on Networking,2007, 15(1): 201-211.

[10] VAN MIEGHEM P, KUIPERS F. Concepts of exact QoS routing algorithms[J]. IEEE/ACM Transactions on Networking, 2004, 12(5):851-864.

[11] GUO Y C, KUIPERS F, VAN MIEGHEM P. Link disjoint paths algorithm for reliable QoS routing[J]. International Journal of Communication Systems, 2003, 16(9): 779-798.

[12] 郭宇春, KUIPERS F, MIEGHEM P V等. 多约束分离路径算法[J].铁道学报, 2005, 27(2): 49-57.GUO Y C, KUIPERS F, VAN MIEGHEM P, et al. Disjoint multiple-constrained paths algorithms[J]. Journal of the China Railway Society, 2005, 27(2): 49-57.

[13] 张品, 张坚武, 李乐民等. QoS约束下的链路分离问题的研究[J].通信学报, 2006, 27(6): 37-42.ZHANG P, ZHANG J W, LI L M, et al. Researches on the problem of link disjoint paths with QoS constraints[J]. Journal on Communications, 2006, 27(6): 37-42.

[14] CHAO P, HONG S. An improved approximation algorithm for computing disjoint QoS paths[A]. IEEE ICN/ICONS/MCL[C]. 2006.

[15] NASER H, GONG M. Link-disjoint shortest-delay path-pair computation algorithms for shared mesh restoration networks[A]. IEEE Symposium on Computers and Communications[C]. 2007. 269-274

[16] XU D H, CHEN Y, XIONG Y Z, QIAO C M, et al. On the complexity of and algorithms for finding the shortest path with a disjoint counterpart[J]. IEEE/ACM Transctions on Networking, 2006,14(1): 147-158.

[17] XIAO Y, THULASIRAMAN K, XUE G L. Constrained shortest link-disjoint paths selection: a network programming based approach[J]. IEEE Transactions on Circuits and Systems-I: Regular Papers, 2006, 53(5): 1174-1187.

[18] BOLLOBÁS B. Random Graphs[M]. MA: Cambridge Univ, Press,2001.