基于模m的n方根的前向安全数字签名方案的分析与改进

刘亚丽，秦小麟，殷新春，李博涵

(1. 南京航空航天大学 信息科学与技术学院，江苏 南京 210016；2. 徐州师范大学 计算机科学与技术学院，江苏 徐州 221116；3. 扬州大学 信息工程学院，江苏 扬州 225009)

1 引言

前向安全数字签名是信息安全风险控制的措施之一，也是目前密码学研究的热点。1997 年，Ross Anderson首次提出前向安全的概念[1]，解决了通常数字签名的一些缺陷：一旦密钥丢失(或被窃取)，由这个密钥生成的以前所有签名都变得无效。Bellare和Miner第一次给出了前向安全签名的正式定义，并基于A.Fiat和A.Shamir的签名方案[2]给出了2个前向安全签名方案[3,4]。前向安全方法的目标是如果在某一时间段签名密钥被盗取，攻击者虽然可以伪造此时段后的签名，但无法伪造密钥被盗取时段前的签名。其思想本质是数字签名安全的风险控制，即将签名密钥被盗后对系统安全所造成的影响和损失尽可能减少到最小。

随着前向安全特性的提出，前向安全数字签名方案已成为信息安全领域的研究热点。Tal M等提出具有无界时间段的前向安全数字签名方案[5]，ANTON K等提出快速密钥更新的前向安全数字签名方案[6]；此外将前向安全特性和其他特殊的签名方案结合，进一步设计具有前向安全特性的特殊数字签名方案，如李如鹏等提出的高效撤销成员的前向安全群签名方案[7]，王晓明等提出的前向安全的多重数字签名方案[8]，彭华熹等提出的基于双线性映射的前向安全门限签名方案[9]等。同时前向安全的概念在电子货币系统[10]、密钥交换协议[11]等方面有着重要的应用。在特定的应用领域如何真正保证前向安全特性，从而提高整个方案的安全性是个亟待解决的问题。近年来众多学者提出的前向安全数字签名方案在密钥的进化上使用最多的是使基于模m的n方根难题[8,9]作为单向函数，实际上具有因子分解难度。如何让密钥演进与签名结合起来是个较难解决的问题，以及如何寻找更多单向密钥更新算法来构造前向安全数字签名方案，均将是今后前向安全数字签名方案值得进一步研究的问题。

基于模m的n方根难题的前向安全数字签名方案[12～18]的共同点是密钥演进均采用求密钥模m的n方根，试图为签名加上一个“时间戳”，防止签名者对先前时间段签名的抵赖。由于可以使用后继密钥的信息对当前时段的消息进行签名，虽然密钥是前向安全的，但是签名却不具备前向安全性，使得密钥的进化没有任何意义。虽然一些学者指出其中某些方案存在的安全漏洞不能抵抗攻击者的攻击，但均没有系统地总结出此类签名方案存在安全漏洞的本质原因。本文针对文献[12～18]提出的一类基于模m的n方根难题的前向安全数字签名方案中的代表方案[12～14]分别进行了详细的安全性分析，发现攻击者如果得到签名者某一签名时段的签名密钥,即可伪造任何签名时段的有效签名(包括此时段前的签名)，得出这些方案[12～18]均不具备前向安全性的结论，进而总结出对于此类前向安全数字签名方案攻击者成功伪造有效签名的本质原因。在实际中，设计前向安全数字签名方案时应注意避免出现此类安全隐患。

本文在总结此类签名方案密钥泄漏根本原因的同时对签名方案[12]进行了改进，采用将当前签名密钥隐藏且仅使用与当前密钥有关的信息进行签名的方式，构造了一种真正具备前向安全特性的新方案，其安全性基于求合数模平方根难度的密钥演进与求离散对数难题签名的结合。通过详细的安全性分析和计算复杂度分析表明新方案不仅具有前向安全性，而且和已提出的改进方案[19]相比减少了求幂运算、乘法运算和加法运算的次数，有效地提高了签名的速度，具有一定的理论意义、安全性和实用性。借鉴对文献[12]的改进方法，根据有限域上数字签名所基于的困难性问题和基于求模m的n方根难度的密钥演进进行方案的设计，使用当前密钥或与当前密钥有关的信息进行签名，将时段信息加入签名（与后继密钥无关），可改进此类基于模m的n方根难题的其他签名方案，真正实现整个签名方案的前向安全性。利用此改进方法的基本思想可以设计前向安全代理签名、前向安全群签名、前向安全多重签名等一些具有实际应用价值的签名方案。

2 前向安全数字签名方案分析

2.1 模m的n方根问题

设n≥2，同余方程xn≡a(modm)称为模m的二项同余方程。当(a, m)=1且m≥2时，若二项同余方程xn≡a(modm)有解，则称a为模m的n次剩余；若无解，则称a为模m的n次非剩余。

特殊地，当n=2且m≥2时，若二项同余方程xn≡a(mod m)有解，则称a为模m的二次剩余；若无解，则称a为模m的二次非剩余。

模m的n次剩余问题也被称为模m的n方根问题。

2.2 基于ElGamal体制前向安全签名方案的安全性分析

具体签名方案请参见文献[12]。此签名方案不具备前向安全性：即若攻击者得到签名者第j(1≤j≤T) 时段的签名密钥SKj，即可伪造任一时段 j' (1≤j'≤T) 的有效签名( j', r, δ )。

若攻击者获得了第j(1≤j≤T)时段的签名密钥SKj，由于( j, r, δ )可以从公用信道获取，所以攻击者可以获知r和δ。签名方通过δ=(H(m)-计算第 j(1≤j≤T) 时段的签名δ 时，根据第 j(1≤j≤T) 时段的密钥更新算法，由SKj+1=mod(p-1)可以得到，因此为一个和时段 j 无关的常数。又由于H(m), r, k, p均和时段 j 无关，所以每一个不同j(1≤j≤T)时段求出的签名δ 也和时段 j 无关，故最终的签名( j, r, δ )中只有表示时段 j 的不同。因此攻击者一旦获得签名者某一签名时段 j(1≤j≤T) 的签名密钥SKj，就可以根据且将签名时段标记换为 j'，即可成功地伪造出任一签名时段 j' (1≤j' ≤T) 的签名( j', r, δ )，这样j(1≤j≤T)时段前的签名也可以通过这种方法伪造出来，所以此签名方案不具备前向安全性。

根据以上分析可得，攻击者一旦获得签名者第j(1≤j≤T) 时段的签名密钥SKj，就可以成功伪造任一时段 j' (1≤j'≤T)的有效签名( j', r, δ )，所以此签名方案不具备前向安全性。

2.3 前向安全可证实签名方案的安全性分析

具体签名方案请参见文献[13]。此签名方案不具备前向安全性：即若攻击者得到签名者第i(1≤i≤T) 时段的签名密钥xsi，即可伪造任一时段 j(1≤j≤T) 的有效签名＜j, SGN( M , xsi), yT＞ = ＜ j,( c, s), yT＞。

基于该方案的攻击和文献[12]的攻击类似。在有效签名＜i, SGN( M , xsi), yT＞ = ＜ i, ( c, s), yT＞中，签名公钥yT=是一个和时段i无关的不变量，签名方计算第 i(1≤i≤T) 时段的签名＜ i, ( c, s),yT＞时，根据第 i(1≤i≤T) 时段的密钥更新算法，由xi=mod N 可以得到又因为进化私钥xsi=xi ，所以为一个和时段i无关的常数，根据进行的验证肯定是正确的。基于以上所述可以得知，若攻击者一旦获得第i(1≤i≤T) 时段的签名密钥xsi，根据可以做出第j (1≤j≤i≤T) 时段的签名，只需计算c= H( M‖g‖yT‖j‖gk)，s=(k-xs2iT-ic)mod N ，其中k从ZN中随机选取，将签名时段标记换为j，j为[1, T]中的任一时段，此时仍然成立，故通过ζ= H(M‖g‖yT‖j‖gsyTc)验证此伪造签名成立。i(1j≤i≤T)时段前的签名也可以伪造，所以此签名方案不具备前向安全性。

在文献[13]中注意到以下特点：签名公钥为PK={g, N, yT}，其中，最终签名为 ＜i,SGN( M, xsi), yT＞ = ＜ i,(c, s), yT＞，其中c = H( M‖g‖yT‖i‖gk)，根据第 i(1≤i≤T) 时段的密钥更新算法mod N，可得，又因为xsi=xi，所以签名中的为一个常数，因此实际签名私钥和时段i无关，验证等式H( M‖g‖yT‖i‖gsyTc)= H(M‖g‖yT‖i‖gk)也和时段i无关。

根据以上分析可得，攻击者一旦获得签名者第i(1≤i≤T) 时段的签名密钥xsi，就可以成功伪造任一时段j(1≤j≤T) 的有效签名＜j, ( c, s), yT＞，所以此签名方案也不具备前向安全性。

2.4 前向安全代理签名方案的安全性分析

具体签名方案请参见文献[14]。此签名方案不具备前向安全性：即若攻击者得到原始签名者A的私钥kA或者代理签名者B的私钥kB，即可伪造任一时段j(1≤j≤T)的有效代理签名[j, (m, s, u,t～)]。

若攻击者获得了原始签名者A的私钥kA或者代理签名者B的私钥kB，由于yA和yB分别为原始签名者A和代理签名者B的公钥，可以从公用信道获取，根据或者，攻击者可以获得初始时段的代理签名密钥σ0，进而通过代理密钥进化算法，即可获得任一时段j(1≤j≤T)的代理签名密钥σj。在有效签名[j,(m,s,u,)]中，，其中，αj,jβ由代理签名者B随机选取，原始签名者A选择一对整数(e,d)使得ed=1modφ(n)，并公布(IDA,yA,e)，代理签名者 B 公布(yB,IDB)。根据可得，因此签名重要参数r,z可以通过上式计算得到，进而签名中u通过散列函数即可得到，攻击者再通过获取的代理签名者B私钥kB可以直接计算出签名s。在验证过程中，根据r'和r的公式，可得

根据以上分析可得，不论攻击者获取原始签名者A的私钥kA还是得到代理签名者B的私钥kB，都可以成功伪造任一时段j(1≤j≤T)的有效代理签名[j,(m,s,u,)]，所以此签名方案也不具备前向安全性。

由于篇幅有限，文献[15～18]安全性分析与2.2～2.4节分析类似，此处不再赘述。

3 密钥泄漏的根本原因分析

综上所述，此类基于模m的n方根难题的前向安全数字签名方案均存在安全隐患，密钥泄露的主要原因如下：

1)密钥演进本质上均为基于求模m的n方根的难题作为单向函数，具有因子分解难度，保证密钥的前向安全性；

2)在最终的签名中均采用私钥 n次方幂的形式进行签名，根据密钥进化算法，使得实际签名的私钥变为一个和具体时段无关的常数，导致私钥的进化对于整个签名方案而言没有任何意义；

3)验证等式均和具体时段无关，使得时段参数不是一个有效的参数。

以上导致前向安全失败的原因中，密钥泄漏最关键的是第2个原因。此类方案的密钥进化算法相同，均为基于求模m的n方根的难题作为单向函数，使得私钥进化是前向安全的；但是在签名过程中采用私钥n次方幂的形式进行签名，根据密钥进化算法，使得整个实际签名的私钥变为一个和时段i(1≤i≤T)无关的常数，导致私钥进化没有任何意义。只要恰当地在实际签名中加入当前时段i (1≤i≤T)的信息，使得进化的私钥真正用于签名，并且验证等式和签名公钥的形式随之改变，就可以实现整个签名方案的前向安全性。

下面从导致前向安全失败最关键的第2个原因入手对基于ElGamal体制的前向安全签名方案[12]进行改进，设计一种真正具备前向安全特性的新方案。

4 基于ElGamal体制的前向安全签名方案的改进

方案定义新的密钥生成算法、密钥进化算法、签名算法与验证算法对原方案[12]进行改进。通过详细的安全性分析可知，改进的新方案真正具备前向安全性，且和夏等人提出的改进方案[19]相比减少了求幂运算、乘法运算和加法运算的次数，从整体上有效地提高了签名的速度。

1) 密钥生成

① 选择一个大素数p和随机数SK0(小于p)，g是GF(p)的生成元；

③ 公开p，g，T和PK。

2) 密钥进化

若j=T+1，则SKj为空串；若1≤j≤T，则。其中j表示第j个时间段。

3) 签名算法

① 签名方选择随机数k∈Zp，计算r = gkmod p；

②签名方选择随机数μ∈Zp，计算ω=SKjgμmodp；

③ 计算δ=(H( m)+2T-jμr) k-1mod(p-1)，其中m为签名消息；

④ 发送 ( j, r,ω, δ ) 给验证方。

4) 验证算法

验证者验证：(PKω-2T-j)rrδmodp=gH(m)mod p。若等式成立，则认可签名( j, r,ω, δ )有效；否则，认为( j, r,ω, δ )是无效签名。

5) 安全性分析

① 有效性

根据方案中相关等式考察签名验证中的等式：

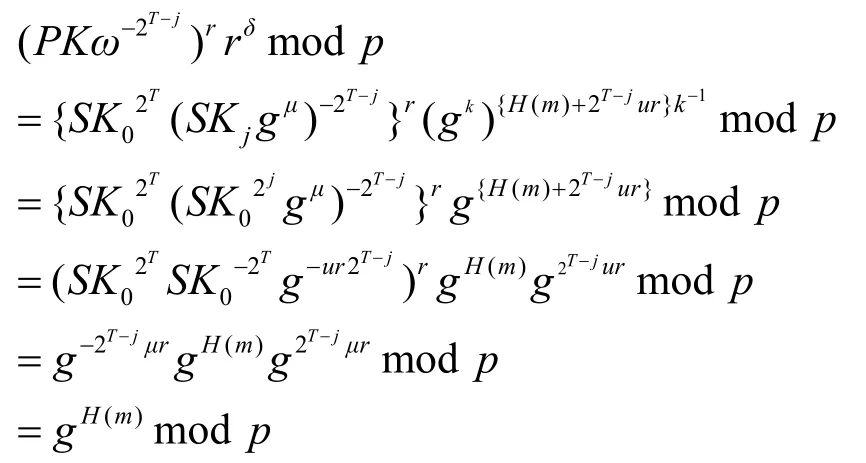
由上式可以得出验证等式

成立，因此本签名方案是正确的，( j, r,ω, δ )为有效的前向安全签名。

② 前向安全性

本方案中签名私钥SKj在签名过程中根据时间段 j(1≤j≤T) 的不同进行更新，而签名公钥PK在整个签名过程中不变。由于采用的密钥进化算法是单向函数，若想通过此密钥进化算法求出j时段之前的私钥是基于求模合数平方根问题的难解性，其困难性等价于因子分解问题，因此私钥SKj的进化具有前向安全性。

在本方案中将签名私钥SKj在签名之初转换为随机的实际签名私钥μ，由信息ω传到验证者证实，传给验证者的信息ω是直接与 j时段密钥相关的信息，即使攻击者盗取了第 j(1≤j≤T) 时段的签名密钥SKj，也最多只能通过密钥进化算法求出j+1时段的密钥SKj+1，再通过δ=(H( m)+2T-jμr) k-1mod(p -1)进而可以伪造j+1时段的签名，但是一定不能伪造密钥被盗取时段j(1≤j≤T) 前的签名，即时段j前的签名仍然有效。

假设j时段的私钥SKj泄露，攻击者伪造 i (i ＜j) 时段的最终签名记为(i, r',ω',δ ')，其中ω'由攻击者随机选取的实际签名私钥μ' ∈Zp，通过mod p 计算得出(SKi'为攻击者伪造的i时段私钥)。由于≠SKi=，故验证过程无法通过，详细过程见③抗伪造性分析。

因此，本方案私钥SKj的进化和 j 时段的签名( j, r,ω, δ )均具有真正的前向安全性。

③ 抗伪造性

信息ω作为签名的重要组成部分在j时段公开，由ω=SKjgμmod p 可知，若想通过ω得到实际签名私钥μ(即隐藏的私钥)是基于离散对数的难题，根本不可行。由ω和δ的公式可知，如果无法知道私钥SKj和μ，则显然也无法构造j时段的有效签名( j, r,ω, δ)；且由验证公式可知，在不知道私钥SKj和μ的情况下，想用一个伪造的私钥SKji'进行签名，则验证无法通过。

假设攻击者伪造i时段私钥SKi'，随机选取实际签名私钥μ'∈Zp构造，进而伪造i 时段的最终签名记为(i, r',ω',δ ')，但是在验证过程中，由于，因此有

因此验证无法通过，本方案具有较强的抗伪造性。

6) 方案特点

本签名方案的特点是将签名密钥 SKj转换为随机的实际签名密钥μ，利用求离散对数的难题隐藏了签名密钥SKj的信息，仅使用与当前密钥有关的信息进行签名，与后继密钥无关，不需要额外的存储空间，使窃密者没有任何可能由后继密钥伪造出前时段的签名信息，且验证等式在ElGamal原等式基础上构造的同时，恰当地加入了时段 j的信息，签名方案的前向安全性基于离散对数问题和模合数平方根问题的难解性。这是本方案和现有的众多前向安全数字签名方案的不同特色所在，从而真正实现了一种基于模 m的二次方根问题的新的数字签名方案的前向安全性，具有一定的理论意义、安全性和实用性。本方案所采用的方法也同样适用于此类基于模m的n方根难题的其他签名方案，由于篇幅的限制，此处不再赘述。

由以上分析可知，设计一个真正具备前向安全特性签名方案的关键在于需在实际签名中加入当前时段 j (1≤j≤T) 的信息，使得进化的私钥真正用于签名，公钥和验证等式的形式随进化的私钥在原有的基础上构造，从而保证当前私钥和验证过程中时段参数的有效性。

7) 计算效率分析

将夏等人提出的改进方案[19]和本文构造的新方案进行比较，并将2种方案的计算量列入表1中进行对比。其中E、M、A、I分别代表取模意义下的求幂运算、乘法运算、加法运算以及逆运算。在签名过程中，这些运算占据大部分的计算时间。通过分析表明，新方案与改进方案[19]相比，除了密钥进化阶段运算量相同，签名过程中的其他各阶段均减少了计算量，所以新签名方案的总运算量比改进方案[19]低，有效地提高了签名的速度。

5 结束语

本文介绍了前向安全数字签名的思想本质、目标和研究现状，分析了近年来众多学者提出的一类基于模m的n方根难题的前向安全数字签名方案的安全性，进而总结出对于此类前向安全数字签名方案攻击者成功伪造签名的本质原因。在实际应用中，设计前向安全数字签名方案时应注意避免出现此安全隐患。同时根据有限域上数字签名所基于的困难性问题，对其中一种签名方案进行了改进，构造一种真正具备前向安全特性的新签名方案，并进行详细的安全性分析和计算复杂度分析。本文的改进方案和已提出的改进方案相比在签名速度上有了明显的提高。本文中改进方案所用的方法也同样适用于此类基于模m的n方根难题的其他签名方案，对于构造其他具有特殊性质的前向安全数字签名方案具有借鉴意义，在实际中具有广泛的应用价值。下一阶段的研究是设计效率更高、安全性更强的、具有实用价值的新型前向安全数字签名方案及其形式化安全性证明，并使得前向安全特性和特殊数字签名技术恰当结合，从而在电子支付系统、移动安全计算、隐私保护等方面得以更加广泛的应用。

[1] ROSS A. Two remarks on public key cryptology[A]. The Fourth Annual Conference on Computer and Communications Security[C]. New York, 1997. 151-160.

[2] AMOS F, ADI S. How to prove yourself: practical solutions to identification and signature problems[A]. Advances in Crytology- Crypto’86,Lecture Notes in Computer Science[C]. Santa Barbara, California,USA, 1987. 186-194.

[3] MIHIR B, SARA K M. A Forward-secure digital signature scheme[A].Advances in Cryptology-Crypto'99, Lecture Notes in Computer Science[C]. Springer-Verlag, Santa Barbara, California, USA, 1999.431-448.

[4] MICHEL A, LEONID R. A new forward-secure digital signature scheme[A]. Advances in Cryptology-Asiacrypt 2000, Lecture Notes in Computer Science[C]. Springer-Verlag, Kyoto, Japan, 2000. 116-129.

[5] TAL M, DANIELE M, SARA M. Efficient generic forward-secure signatures with an unbounded number of time periods[A]. Advances in Cryptology-EUROCRYPT 2002, Lecture Notes in Computer Science[C]. Springer-Verlag, Amsterdam, The Netherlands, 2002.400-417.

[6] ANTON K, LEONID R. Forward-secure signatures with fast key update[A]. Proc of the 3rd International Conference on Security in Communication Networks[C]. Springer-Verlag, Amalfi, Italy, 2003.241-256.

[7] 李如鹏,于佳,李国文等. 高效撤销成员的前向安全群签名方案[J].计算机研究与发展, 2007, 44(7): 1219-1226.LI R P, YU J, LI G W, et al. Forward secure group signature schemes with efficient revocation[J]. Journal of Computer Research and Development, 2007, 44(7): 1219-1226.

[8] 王晓明, 符方伟, 张震. 前向安全的多重数字签名方案[J].计算机学报, 2004, 27(9): 1177-1181.WANG X M, FU F W, ZHANG Z. A forward secure multisignature scheme[J]. China Journal of Computers, 2004, 27(9): 1177-1181.

[9] 彭华熹, 冯登国. 一个基于双线性映射的前向安全门限签名方案[J].计算机研究与发展, 2007, 44(4): 574-580.PENG H X, FENG D G. A forward secure threshold signature scheme from bilinear pairing[J]. Journal of Computer Research and Development, 2007, 44(4): 574-580.

[10] 苏云学, 祝跃飞. 一个前向安全的电子货币系统[J]. 计算机学报,2004, 27(1): 136-139.SU Y X, ZHU Y F. A forward-secure e-cash system[J]. China Journal of Computers, 2004, 27(1): 136-139.

[11] 吴树华, 祝跃飞. 一个前向安全的基于口令认证的三方密钥交换协议[J]. 计算机学报, 2007, 30(10): 1833-1841.WU S H, ZHU Y F. Three-party password-based authenticated key exchange with forward-security[J]. China Journal of Computers, 2007,30(10): 1833-1841.

[12] 吴克力, 王庆梅, 刘凤玉. 一种具有前向安全的数字签名方案[J].计算机工程, 2003, 29(8): 122-123.WU K L, WANG Q M, LIU F Y. A forward security digital signature scheme[J]. Computer Engineering, 2003, 29(8): 122-123.

[13] 秦波, 王尚平, 王晓峰等. 一种新的前向安全可证实数字签名方案[J]. 计算机研究与发展, 2003, 40(7): 1016-1020.QIN B, WANG S P, WANG X F, et al. A new forward-secure and confirmer digital signature scheme[J]. Journal of Computer Research and Development, 2003, 40(7): 1016-1020.

[14] 王晓明, 陈火炎, 符方伟. 前向安全的代理签名方案[J]. 通信学报,2005, 26(11): 38-42.WANG X M, CHEN H Y, FU F W. Forward secure proxy signature scheme[J]. Journal on Communications, 2005, 26(11): 38-42.

[15] 谭作文, 刘卓军. 一个前向安全的强代理签名方案[J]. 信息与电子工程, 2003,1(4): 257-259.TAN Z W, LIU Z J. A forward secure strong proxy signature[J]. Information and Electronic Engineering, 2003, 1(4): 257-259.

[16] 夏祥胜, 耿永军, 洪帆等. 前向安全的有代理的多重数字签名方案[J]. 小型微型计算机系统, 2009, 30(5): 854-858.XIA X S, GENG Y J, HONG F, et al. Forward secure multisignature with proxy signers scheme[J]. Journal of Chinese Computer Systems,2009, 30(5): 854-858.

[17] 彭仁杰, 杨小东. 基于 Euler准测的前向安全的数字签名方案[J].计算机应用与软件, 2009, 26(4): 260-261.PENG R J, YANG X D. A forward secure digital signature scheme based on Euler’s criterion[J]. Computer Applications and Software,2009, 26(4): 260-261.

[18] 王玲玲, 张国印, 马春光. 标准模型下基于双线性对的前向安全环签名方案[J]. 电子与信息学报, 2009, 31(2): 448-452.WANG L L, ZHANG G Y, MA C G. A forward-secure ring signature scheme based on bilinear pairing in standard model[J]. Journal of Electronics & Information Technology, 2009, 31(2): 448-452.

[19] 夏峰, 谢冬青, 匡华清. 一类前向安全数字签名方案的分析与改进[J]. 计算机工程, 2006, 32(16): 146-147.XIA F, XIE D Q, KUANG H Q. Analysis and improvement for a class of forward security digital signature scheme[J]. Computer Engineering,2006, 32(16): 146-147.