基于改进隐马尔可夫模型的网络攻击检测方法

杨晓峰，孙明明，胡雪蕾，杨静宇

（南京理工大学 计算机系，江苏 南京 210094）

1 引言

网络服务器需要被互联网上的任何人访问，大量的网络应用服务的开发者对安全意识的缺失，致使网络服务存在大量的漏洞，网络服务器也成了黑客攻击的主要目标。最新的CVE漏洞趋势报告[1]显示，跨站脚本攻击（XSS）、SQL注入（SQL-injection）和远程文件包含（RFI）3种典型的基于 HTTP协议[2]的网络攻击已经占了近年来漏洞攻击总数的一半。

入侵检测[3]是防御网络攻击的主要手段。入侵检测系统（IDS，intrusion detection system）通过对网络数据流或访问记录的分析，识别和发现带有攻击性的网络行为。入侵检测主要分为2大类：误用检测（misuse detection）和异常检测（anomaly detection）。误用检测定义攻击行为的特征，提炼攻击行为的特征写成规则进行检测匹配。这种方法的缺点是需要对每一种攻击方式书写准确的规则，因为攻击手段越来越趋于多样化，规则数量变得非常庞大。例如Snort[4]的规则数量已经从几年前的1 000多条增加到现在的8 000多条，保证这些规则的准确性和低误报率十分困难。另外，这种检测方式无法检测到新的攻击方式。

异常检测可以有效地克服误用检测的缺点。异常检测定义正常行为的特征，通过统计、数据挖掘的方法，针对正常行为学习特征模型，当网络行为显著偏离正常的行为模式时识别为异常行为。在复杂的攻击检测任务，如针对 DDoS（分布式拒绝服务）攻击[5,6]的检测方面具有相对于误用检测的很大的比较优势。

本文提出了一种新的基于改进隐马尔可夫模型的异常检测方法。基于HTTP协议的访问可以看作是一个字符串序列，正常访问产生的字符串序列符合一定的语法规则，以有序的方式组合出现，而异常的攻击行为与正常的语法规则差距很远，用户访问符合这种语法的程度可以作为一个合适的度量区别正常与异常的行为。针对现实数据的对比实验结果显示，这种方法大大提高了检测率，同时保持了较低的误报率。

2 相关研究工作

隐马尔可夫模型善于处理序列型数据，在语音识别方面有很成熟的应用。文献[7,8]提出用隐马尔可夫模型检测进程是否异常的方法。算法以进程的系统调用序列建立模型，当某个进程的系统调用序列显著偏离正常状态（即序列概率明显偏小）时，判定此进程为非法进程。文献[9]将隐马尔可夫模型运用到异常用户行为的识别中，算法从用户的Shell命令序列中提取特征。这2种方法都只能做基于主机的异常检测，应用范围受到很大的限制。

文献[10]中提出基于隐马尔可夫模型的分布式拒绝服务攻击的检测方法。该方法集成了4种不同的检测模型以对付不同类型的攻击，通过从数据分组中提取TCP标志位、UDP端口和ICMP类型及代码等属性信息建立相应的TCP、UDP和ICMP的隐马尔可夫模型，用于描述正常情况下网络数据包序列的统计特征，然后用它来检测网络数据包序列，判断是否有DDoS攻击。这种方法是基于网络层协议的检测，同时只能检测单一的DDoS攻击，无法检测当下流行的基于应用层协议的攻击。

文献[11]提出了将隐马尔可夫模型用于基于HTTP应用层协议的异常检测方式。HTTP协议的攻击一般由非法的字符串请求组成，作者抽取字符序列建立隐马尔可夫模型。根据HTTP请求的特点，算法按请求中不同的属性分类，从每一类的正常请求样本中学习得到的语法规则，以隐马尔可夫模型表示。这种方法可以自动学习应用程序的正常访问模式，但检测性能很差容易产生较高的误报率[11,12]。

本文改进了这一模型，提出了一种改进的隐马尔可夫检测算法，大大提高了算法在HTTP请求异常检测中的检测性能。

3 基于改进HMM的检测算法

3.1 数据模型

本文的数据来源于Web服务器的log（log信息包含访问时间、访问的网站名称、IP、访问方法、路径和参数等），如图 1所示。提取特征 f={path,(a1,v1),(a2,v2),…,(aN,vN)}，其中 N=0,1,2…。参数由属性组成，以“属性名=属性值”的形式组织。

3.2 HMM的数学基础

X表示训练样本集，XP和XN分别为X中标记为正常和异常的训练样本。

基于隐马尔可夫模型的语法由一个三元组表示： M = ( Q,T,E)，Q是状态集，T是状态转移矩阵， p (qi-＞qj)=T(qi, qj)是状态qi到qj的转移概率；E是状态输出矩阵， p ( qi↑ si)= E(qi,si)是状态qi输出为si的概率。定义2个特殊状态I和F，分别为初始状态和终止状态，即每一个被M所接受的语句都必须以I开始和F结束。

对于任意样本sT，定义P(sT|M)为由M产生sT的概率

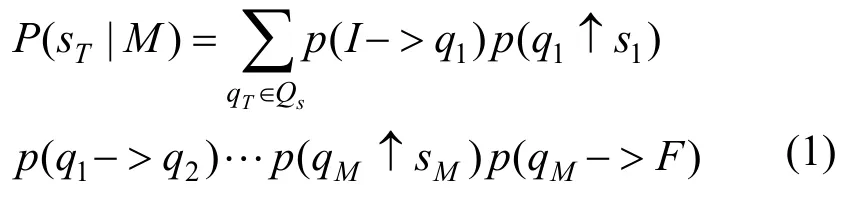
其中，sT=s1s2…sM，qT=q1q2…qM是sT的状态序列，Qs是sT所有可能的状态序列集合。

3.3 学习算法

算法的学习过程需要学习语法 M 和分类阈值a0，如图2所示。语法M是能最优代表正常训练样本集XP语法的HMM模型。本文根据M产生样本的概率，提取样本的异常测度，结合标记的训练样本学习最优的区分正常和异常样本的分类阈值a0。

图1 log样例

图2 学习算法

3.3.1 基于HMM的属性值语法学习

从正常训练样本集XP建立初始模型M0的过程比较简单，如图3(a)所示，每个样本字符串可以看成一个全新的状态序列，每个状态以概率1输出对应字符，前一个状态以概率1转移到后一个状态，序列的前后分别连接到初始状态I和结束状态F。I到所有样本首状态的概率为1/N，其中N为XP的样本数量。

M0忠实的反应了XP包含的语法信息， 任意样本 x，如果 x ∈ XP，则 P (x|M0) ∈ (0,1)，表示 x被M0接受，大小与x在XP中的重复次数成正比；如果x∈ XP，P(x| M0)=0，表示 x被 M0拒绝。当XP完整的包含了所有正常状态的时候，M0是一个理想的语法；但当 XP只包含部分正常样本的时候，M0会拒绝其它未列入 XP的正常输入。而希望学习到的 M，可以最优的代表 XP所属的一大类正常样本的语法结构，所以引入模型 M0的简化和提炼，以得到最优语法M。为了表示方便，在本节中余下的部分，用X表示待学习的正常训练样本。

根据贝叶斯原则，算法取使得在X的条件下后验概率最大的M作为最优标准，即学习使得P(M|X)最大的M，此时认为M是最可能产生X的语法。P(M|X)计算如下：

P(X)可以看作是一个常数，所以得到

P(M|X)取最大，等价于P(X|M)P(M)取最大。问题转换为在 M 的取值空间内选取使式(3)达到最大的M。当M已知，P(X|M)的计算等于所有X中元素概率P(xi|M)的乘积。

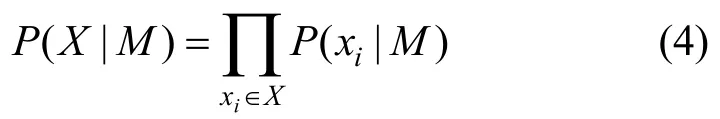
其中P(xi|M)则可以利用式(1)计算。

P(M)是模型本身的先验概率，对它的理解不是很直观。文献[13,14]指出，简单的模型应该具有更高的先验概率。模型M的复杂度又由模型中的状态数N、状态转移的数量NT和状态输出的数量NE决定。文献[11]中取

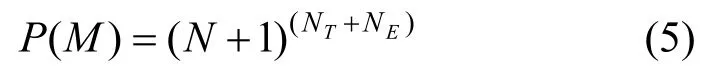
给定一个状态数为N的隐马尔可夫模型M0，在 M的取值空间内搜索使得后验概率 P(M|X)最大的最优模型M是一个很困难的问题。首先M的取值空间极其复杂，难以清楚定义；其次即使定义了M的取值空间，遍历空间中的每一个M的取值计算最优P(M|X)也不现实。方法采取搜索局部最优值的策略求解最优语法模型M。

模型M的求解是一个迭代的过程，从初始模型M0开始，每次迭代过程将2个状态合并，直到式(3)不再增加。每一步迭代选取使得式(3)增长最快的状态对合并。假设求解M的迭代序列是M0, M1,…, Mk,Mk+1,…，当出现 P(Mk+1|X)＜ P(Mk|X)时，则 Mk就是要求的最优模型M。

图3是正常训练样本集为{abc，acba}的M学习过程。搜索最优M的过程可以视为搜索局部最大值的过程，当下一步的局部最大值比当前值小的时候停止搜索。如图 3(f)的后验概率比图 3(e)小，则搜索停止，得到图3(e)为局部最优的M。同时，求解M的过程也是语法提炼和一般化的过程，通过对M0的一般化，使得模型M可以接受更多的语法输入。例如图3(c)已经可以接受“aba”、“acbc”等不同于训练样本的输入，图3(d)、图3(e)则更多。

3.3.2 改进的HMM学习方法

本文的算法改进包括下面的公式修改和多处优化。

模型 M 的先验概率计算从式(5)改成了如下的式(6)：

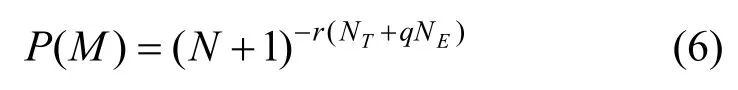
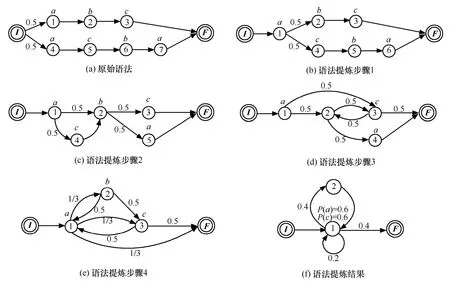
图3 M学习过程

其中，q为NT相对于NE的影响因子，r为P(M)相对于P(X|M)的影响因子，q、r都为正常数，一般取1。根据文献[13,14]中提出的简单模型具有更高的先验概率的原则，式(5)并不符合这一原则。当N、NT、NE变小的时候，即 M 变得更为简单时，式(5)中P(M)变小趋向于1；反之修改的式(6)中P(M)变大趋向于1，更为合理。参数q、r的引入，使得在M的迭代搜索过程中，可以控制边相对于发射状态的优先权，同时可以控制 P(M)相对于 P(X|M)在后验概率计算中的权重，从而影响搜索过程的停止条件。

算法优化如下。

1) 优化状态合并

在合并状态时采取优先合并具有相同发射状态的节点的策略，这种策略的合理性解释如下。如图4所示，当状态2、5合并的时候，导致P(X|M)减小，P(M)增大，后验概率增减主要由P(X|M)减小的量决定。减小的差值可以表示为 Δ =(1-α)P1P2P3P4C，其中α=，C为与被合并状态无关的常数，wi为每个状态积累的权重，即这个状态表示的样本数量。当状态2、5的发射状态a、b相等的时候，P(a)=P(b)=1，取值增大，从而使 P(X|M)减小的量变小，最终使后验概率P(M|X)增大。特别同时当w1=w2时，α=1，P(X|M)单调递增。

需要指出的是，优化的合并策略并不保证后验概率P(M|X)在每一步迭代中都增大，甚至会略有减小。这样做的好处是简化了优化搜索的复杂度，弱化了局部最优值对全局最优值搜索的影响，增强了算法的对语法的抽象能力。在本文的实验中可以看出，这一对抽象能力的增强不但提高了算法的检测率，同时也没有引进很高的误报率。

2) Viterbi路径代替所有可能的路径

在式(1)中 M 产生某个样本的概率是所有可能的路径qT的概率和，定义为样本sT的Viterbi路径，即sT最有可能的状态路径。所以式(1)更新为

图4 状态的合并

其中qT=q1,q2,…,qM是sT的Viterbi路径。

3) 分组渐进的压缩策略

假设训练样本集X的容量为k，模型的状态数为n，在无法满足优化条件的情况下，单步压缩模型M的复杂度大于Ο(kn3)，当n很大时的计算量极大，这就要求把n控制在一个比较合理的数值以内。

用分组渐进压缩的方法，一个大型的模型 M 分割为一组大小合适的子模型，分别局部优化，最终将优化好的子模型组合进行全局优化。实验中发现当n控制在200以下的时候可以得到较好的计算速度。

3.3.3 学习分类阈值

定义样本sT对于语法模型M的异常测度为

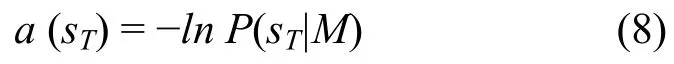
因为 P(sT|M)取值范围是[0,1]，所以 a(sT)的取值范围是[0,+∞)，当sT是正常行为，异常测度越趋近于0，否则越趋近于+∞；特别是当sT不能被M接受时， a ( sT)=+∞。

异常检测是一个2类分类问题，用语法M计算异常测度是提取特征的过程，还需要在训练样本的特征空间学习最优的分类界面。因为特征是一维向量，所以分类界面退化成了最优分类阈值a0，本文采用训练集的最小分类误差标准确定a0。

假设X0、X1为正常和异常类，P(X0|X1)为X1中样本被误分类为X0的概率，则

3.4 检测算法

学习得到语法M和分类阈值a0，检测过程就变得比较简单。如图5所示，检测前用语法M计算待检测样本的异常测度a，再与分类阈值a0比较即可区分行为的正常还是异常。如果a≤a0，判断正常，a＞a0则异常。

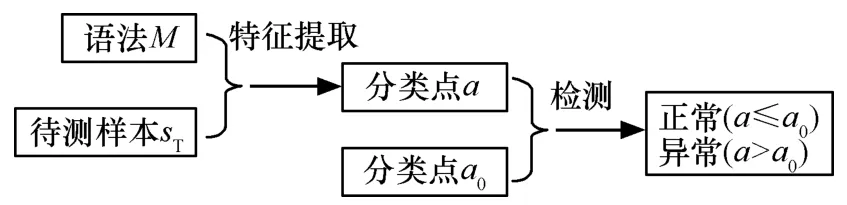
图5 检测算法

对于一个log记录可能存在多个属性，每个属性都会检测出各自的异常结果，只要有一个属性检测出异常，可以认为这个log对应的行为异常。

4 实验和结果

本节用真实的网站log数据来验证本文算法的有效性。实验数据来自于域名为“oldjun.com”网站从2008年9月28日到2009年1月11日的全部访问log。实验数据集含有400M的文本数据。经过人工和程序辅助的检查，含有大量的恶意的攻击访问，其中包括SQL注入、跨站脚本攻击（XSS）、文件包含、漏洞溢出等。

因为不同的路径需要不同的语法M提取特征，也需要不同的分类器作分类检测，所以选择了数据集中具有较大访问量和较多非法攻击的几类路径的访问记录作实验数据集。针对文中算法的特点，实验中过滤了数据集中参数不符合“属性=属性值”类型的数据。表1列出了各数据集的详细信息。

表1 实验数据信息

再将本文的算法（improved HMM）与原来的HMM 算法，以及基于长度和基于枚举类型的算法在不同数据集上做检测性能比较。需要说明的是在HMM算法实现中，本文还是采用了式（6）中的修正后的后验概率计算方式。在每个数据集的一半样本（随机分配）作为训练数据集，另一半作为测试数据集。图6中各分图是不同的检测方法在各数据集的测试集上得到的ROC曲线。

从图6中可以看出，改进HMM和HMM算法的 ROC曲线始终紧贴上边沿，表明可以得到较好的分类性能。其他方法的检测性能在不同数据集上差异很大，但总体要比基于HMM的方法差不少。使用最小分类误差的方法作检测实验，每个数据集随机分成2组，一组作为训练集，一组作为测试集，测试10次取平均，得到表2的检测结果。

实验结果显示，改进HMM方法的检测率要大大好于其他方法，始终保持在95%以上；在大多数数据集上，改进HMM的误报率也要略高，但是在可接受范围内。在数据集D上改进HMM的误报率达到了50%以上，超出根据ROC曲线得出的直观结论。这反映了在小数据集上，训练集和测试集的差异性比在大数据集上大，这种差异对本文的方法具有比其他方法更大的影响；同时反映了本文的方法更适用于在大数据集上的学习、检测应用。

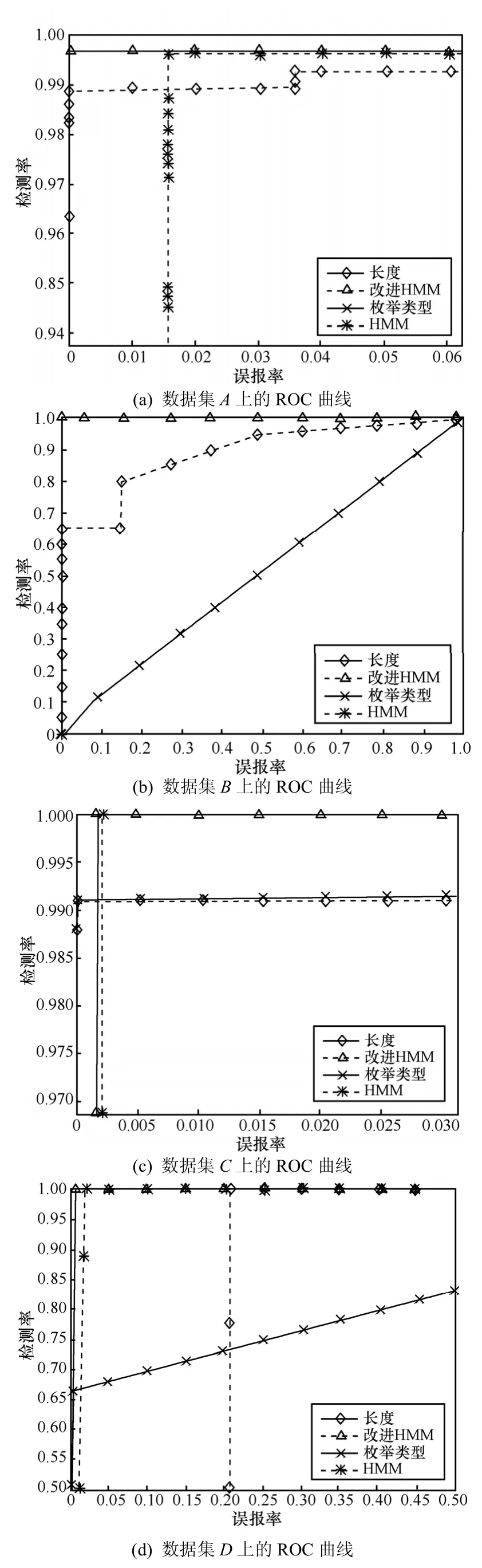
图6 不同检测方法的ROC曲线

表2 检测结果

传统的HMM方法在修改后验概率计算公式后的检测性能要明显优于基于长度和基于枚举类型的异常检测算法。本文在算法改进中提出的优化合并策略在一定程度上增强了算法的抽象能力，提高了检测率，同时保持了较低的误报率。

基于HMM方法的良好的检测性能，源于HMM模型对离散时间序列数据的良好的描述和鉴别能力。字符串类数据的语法可以由HMM模型精确的表示。同时发现对语法抽象能力的增强，可以提高检测率；基于HTTP的检测任务的误报率对于语法抽象的增强不敏感，受到影响很小。

5 结束语

本文提出了一种基于改进隐马尔可夫模型的语法学习的异常检测方法。算法通过对正常 HTTP请求模式的学习，可以有效地检测恶意的攻击行为，大大提高了针对HTTP协议的攻击的检测性能。

隐马尔可夫模型的训练需要很大的计算量，训练时间较其他方法过长；而且训练样本较少时检测性能也会受到很大的影响。加快模型的训练速度和提高算法在训练样本较少情况下的检测性能是今后研究工作的重点。

[1] CHRISTEY S, MARTIN R A. Vulnerability type distributions in CVE[EB/OL]. http://cwe.mitre.org/documents/vuln-trends.html. 2009.

[2] FIELDING R, GETTYS J, MOGUL J, et al. Hypertext Transfer Protocol-HTTP/1.1[S]. RFC-2616, 1999.

[3] BACE R. Intrusion Detection [M]. Macmillan Publishing Co. Inc.,2000.

[4] ROESCH M, Snort-lightweight intrusion detection for networks[A].Proc of the 13th USENIX Conference on System Administration(LISA)[C]. Seattle, USENIX Association,1999. 229-238.

[5] LI M, ZHAO W. Detection of variations of local irregularity of traffic under DDOS flood attack[EB/OL]. http://www.hindaui.com/journals/mpe/2008/475878.html.2008.

[6] LI M. Change trend of averaged Hurst parameter of traffic under DDOS flood attacks[J]. Computers & Security, 2006, 25 (3): 213-220.

[7] WARRENDER C, FORREST S, PEARLMUTTER B. Detecting intrusions using system calls: alternative data models[A]. Proceedings of the IEEE Symposium on Security and Privacy[C]. Oakland, 1999.133-145.

[8] YEUNG D Y, DING Y. Host-based intrusion detection using dynamic and static behavioral models [J]. Pattern Recognition, 2003, 36:229-243.

[9] 邬书跃, 田新广. 基于隐马尔可夫模型的用户行为异常检测新方法[J]. 通信学报, 2007, 28(4): 38-43.WU S Y, TIAN X G. Method for anomaly detection of user behaviors based on hidden Markov models[J]. Journal on Communications, 2007,28(4): 38-43.

[10] 周东清, 张海锋, 张绍武等. 基于HMM的分布式拒绝服务攻击检测方法[J].计算机研究与发展, 2005, 42(9):1594-1599.ZHOU Q D, ZHANG H F, ZHANG S W, et al. A DDos Attack Detection Method Based on Hidden Markov Model.[J]. Journal of Computer Research and Development, 2005, 42(9):1594-1599.

[11] KRUEGEL C, VIGNA G. Anomaly detection of web-based attacks[A].Proc of the 10th ACM conference on Computer and communications security[C]. Warshington, DC. ACM Press, 2003.251-261.

[12] INGHAM K L, INOUE H. Comparing anomaly detection techniques for HTTP[A]. Recent Advances of Intrusion Detection(RAID)[C].Gold Goast, Australia. Springer, 2007.42-62.

[13] STOLCKE A, OMOHUNDRO S. Inducing probabilistic grammars by Bayesian model merging[A]. Conference on Grammatical Inference[C]. London UK. Springer, 1994. 106-118.

[14] STOLCKE A, OMOHUNDRO S. Hidden markov model induction by bayesian model merging[A]. Advances in Neural Information Processing Systems[C]. San Fancisco, CA. 1992. 11-18.