职高数学课激趣方法初探

鲁军兵

（余姚市职成教中心学校 浙江 余姚 315400）

职高数学课激趣方法初探

鲁军兵

（余姚市职成教中心学校 浙江 余姚 315400）

职高学生在学习数学时存在着种种问题，表现为自信心不强、对数学不感兴趣、数学思维能力差等。调动学习动机和学习兴趣是解决问题的关键。只有提高他们学习数学的兴趣，他才能好学、乐学。本文就如何在课堂教学中激发学生的兴趣提出了建议。

职高数学；引趣；激趣；留趣

近年来，随着中职生源素质下降，部分学生在学习数学时出现了种种问题，表现为自信心不强、对数学不感兴趣、数学思维能力差等。前苏联著名教育实践家和教育理论家苏霍姆林斯基认为：“培养学生参与的兴趣是教育的主要策略。”英国现代教育家斯宾塞也强调“教育要使人愉快，要让一切教育带有乐趣”。兴趣带来快乐，快乐产生热爱之情，“兴趣是最好的老师”。学习兴趣是克服学生数学学习困难的内在动力，学生所学材料或研究对象生动有趣，有助于使学生从“要我学”转变成“我要学”，从而有可能获得最佳的教学效果。

数学教师要时时注意教学过程的每一处环节：教学设计要生动活泼，富有创意，具有开放性、启迪性的特点；教学环节要巧妙质疑，设置悬念，启发想象，活用媒体，运用各种激趣手段来激发学生的学习兴趣，使学生主动积极地参与教学活动。激趣有法，然无定法。现就如何在课堂教学中激发学生的兴趣提出几点建议。

课前引趣，导入新课

良好的开端是成功的一半。上课开始，教师应该用最精练的语言，最短的时间，最有效的方法，把学生的情绪调整到最佳的学习状态。这一环节不仅是教师匠心艺术的再现，更是学生认知过程的心理需要。在教学活动开始之际，学生普遍存在上好课的动力准备，心理学称此现象为“心向”。这种心向既强烈，又短暂。一个好的导入设计，能使这堂课先声夺人，引人入胜，更重要的是，能激发学生的学习兴趣和旺盛的求知欲，创造良好的学习氛围，使学生以最佳的状态进入课堂。因而，教师要重视导入设计，以精湛的导入愉悦学生的耳目，激动学生的心灵，开发学生的智力，触发学生的情思。

游戏引趣 在讲数列之前，教师带学生先做游戏。游戏是这样进行的：盒中有100颗糖果，甲、乙二人轮流从中摸出若干颗。规定每次最多摸10颗，最少摸1颗。谁摸到最后一颗为输。教师和一个学生一起来做此游戏，并由学生先摸。于是，一场游戏在众目睽睽之下开始了。教师与学生每次摸出糖的颗数，在黑板上计录如下：1（生）、10（师）；3、8；2、9；4、7；5、6；8、3；9、2；10、1；1、10；1、0。当学生无可奈何地从盒中摸出最后一颗糖时，全班哗然。此时，问学生：“谁能说出我获胜的秘诀在哪里？”当学生纷纷议论之后，教师指着黑板上那列数说：“我获胜的诀窍就在这个数列中，你们谁能说说这列数的规律？”惊讶的学生开始仔细观察黑板上的数。几分钟后，学生回答：“老师我知道了，你们两人每次轮流摸糖的个数的和始终为11。”我说：“正是，了解数列规律是我取胜的关键所在。让我们共同认识一下数列和他们的规律。”全班学生兴趣盎然，一堂课就这样开始了。

联系生活实际引趣 在讲授函数单调性这节课时，笔者设计这样的情境：教师元旦打算去四明山旅游，但是担心天气问题。为预测当天的天气情况，研究去年元旦当天天气情况图，捕捉信息。多媒体技术展示图像，引导学生发现图像的变化趋势（上升或下降）。问题一：在生活中，我们关心很多数据的变化规律，了解这些数据的变化规律对我们的生活是很有帮助的，我们还能举出生活中其他数据变化情况吗？问题二：图像表示的是时间与气温的函数关系，那么从函数观点看，随着自变量的变化，函数值是变大还是变小？生活问题情境的创设，引入自然合理，考虑到学生的“最近发展区”又充分利用了多媒体技术，通过信息技术与数学课程的整合，调动了学生学习的兴趣。图像的直观性又增强了学生对概念的感性认识，把这个以往教学中难以呈现的问题较好地解决，并从中体验概念产生的必要性和价值，引领后续教学。

故事引趣 通过讲故事的方法导入新知识。如讲 “排列”时，笔者从“田忌与齐王赛马”的故事入手，然后启发学生：田忌的马按“好、中、差”与按“差、好、中”两个不同顺序出场，结果完全不同。这是三匹马的两个不同排列。接下去学习“排列问题”，效果非常好。

联系专业引趣 让学生在巩固专业理论基础知识的同时创设情境，深化学生对专业课程的学习，激发学生学习数学知识的主动性和积极性。例如，在学习余弦定理这节课时，教师展示曲柄连杆机构的模型，大屏幕展示横截面图示（见图1）。结合专业，提出曲柄连杆机构的工作原理及其组件AB和BC的名称。问题：（1）请学生说一说曲柄连杆在运动过程中的动点与定点，并说明作了哪几类运动？（2）曲柄连杆机构在运动过程中，线段AB、BC、CA中，哪些线段的长度在变化？（3）若在三角形 ABC中， 已知连杆 AB长为340mm， 曲 柄 CB长 为85mm，曲柄CB与连杆AB的夹角为80°时，求AC的长。这个问题的本质是：已知条件是三角形中的两边AB、CB的长及AB与CB的夹角∠ABC，求三角形中边AC的长。从而引出课题，接下来的学习学生积极性很高。

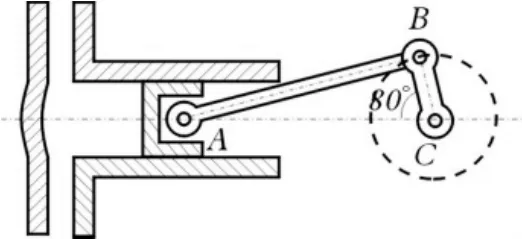
图1 曲柄连杆机构模型图

课中激趣，深究知识

怎样才能使学生保持浓厚的兴趣参与教学活动，理解概念知识呢？单靠有趣的导入是不行的。职高学生活泼好动，注意力保持时间不长，易受外界影响，要他们保持浓厚的学习兴趣，教师必须在课堂教学中把握教材内容，结合学生心理特点，选择生动有趣、富有感染力的方式方法调动学生的学习积极性，使他们主动学、乐意学。

设置思维障碍，激发兴趣 在教学中可有意识地设置思维障碍，使学生产生“山重水复疑无路”之感，然后经过教师的启发诱导，学生的思维便会活跃起来，通过思考找到解决问题的途径，达到“柳暗花明又一村”的境界，从而体验到学习数学的喜悦和成功感。如在学习“等差数列的前n项和”这节课时，先提出问题1+2+3+…+100=？学生马上会想到利用高斯的算法进行计算，然后再适时提出1+2+3+…+21=？还能用高斯的办法计算吗？学生发现高斯的方法只能解决偶数项的求和。这时教师就引导学生积极想办法扫除这个障碍，想到用倒序相加的办法，这样立“障”除“碍”，既使学生主动获得新知识，又稳定了他们的学习兴趣。

操作实验，激发兴趣 著名的瑞士心理学家皮亚杰认为：“思维是从动作开始的，切断了动作与思维之间的联系，思维就得不到发展。”这就要求教师在教学时结合教学内容，为学生创设动脑、动口、动手的机会，通过学生自己动手操作获得知识。学生在实践中学习，更易在激发兴趣的同时掌握知识与技能。例如，在讲“线面垂直的判定定理”的概念时，教师为帮助学生掌握概念的本质属性，可设计这样一个实验：折纸试验（如图2），请学生拿出准备好的一块任意三角形的纸片，首先过△ABC的顶点A翻折纸片，得到折痕AD，将翻折后的纸片竖起放置在桌面上，（BD、DC与桌面接触）。观察并思考：折痕AD与桌面垂直吗？如何翻折才能使折痕AD与桌面所在的平面垂直？多媒体演示翻折过程。同时，归纳直线与平面垂直的判定定理，首先思考：由折痕AD⊥BC，翻折之后垂直关系，即AD⊥CD，AD⊥BD发生变化吗？由此你能得到什么结论？然后再归纳出直线与平面垂直的判定定理。安排折纸试验，讨论交流，给学生充分活动的时间与空间，帮助学生从实践中获取知识，使学生更好地参与教学活动，活跃思维，体验探索的乐趣，增强学习数学的兴趣。这样通过实验总结出的定义，学生印象比较深刻。

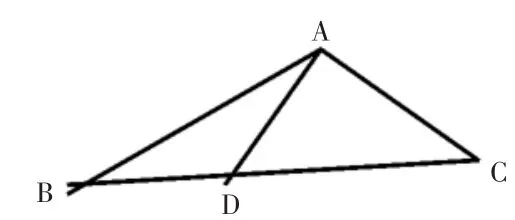
图2 折纸试验图

形象语言，激发兴趣 教学中尽量使用贴近生活、学生熟悉的语言进行讲述，使学生对第一次接触而又抽象的概念有明确具体的认识。例如，在讲分数指数幂化成根式时，即学生对m、n的位置总是糊涂，笔者就形象地讲了一个记忆方法， 分子、分母比喻为母子，而母亲要护着孩子，所以，分母n在外面，分子m在里面了。这种比喻可能不恰当，但是学生容易记忆，而且能产生学习的兴趣。又如，在讲二次曲线离线率的概念时，在学习了教材中定义后，仍有学生记不清还是为了一下子让学生掌握，可讲这样的一些社会现象：上层人物过得好，生活优裕，只有他们才喜笑颜开，而下层的劳苦大众过得累、辛苦，甚至悲哀，即__正适合字母的读音，又易记，又形象。

直观形象，激发兴趣 数学的高度抽象和很强的逻辑推理，往往使许多学生尤其是基础不够扎实的职校学生望而生畏。为排除这种心理，教师可采用“数形结合”的方法，在教学的全过程充分利用直观因素、形象因素、直观教具、教学图表等，使学生清楚地看出，数学知识虽然以高度抽象的形式出现，但这只是在表面上掩盖它起源于外部的实质。而这一切都在教师的启发下，给学生抽象的思维提供了具体的起点。这种通过学生自己实地观察和试验，归纳和类比对数学知识进行学习和研究的方法，是培养学生学习积极性、启发他们积极思维的好方法。例如，在讲“映射”时，在讲完“映射”概念并做了必要的说明后，笔者演示了一张幻灯片：一箱子弹（A），一杆枪（F），一面足够大的墙作为靶子（B），并依序提问：（1）A中的一粒子弹经过枪F发射出去后，假如射中B，B上有几个枪眼？（答：一个且唯一）；（2）可不可能几个子弹射中同一个枪眼？（答：可能）；（3）一粒子弹射出后B上是否可能射出两个或更多个枪眼？（答：不可能）；（4）这次演示中枪靶B上的每个枪眼，都是A中的子弹射出的，对不对？（答：对）。最后，笔者说，假如一粒子弹装入枪膛，勾动扳机后，发现B上没有射出枪眼，可能有那些原因？学生七嘴八舌地答：射飞了、枪坏了、子弹是坏的。笔者说，这是个没用的枪，扔给敌人吧，（这不是映射）；接下来引导学生对照体会映射的定义。形象直观的比喻，使得学生学习兴趣盅然，且不易忘记。

课末留趣、巩固知识

要想学生在一节课里，从头到尾保持浓厚的兴趣。在课末巩固这个环节中，更需要千方百计地设计一些有趣的教学活动来吸引学生的注意力，使他们学了还想再学。例如，在学习了充分必要条件后，可设计这样的课后练习：探究下列生活中名言名句的充要关系：水滴石穿，骄兵必败，有志者事竟成，头发长、见识短，名师出高徒。让学生从数学的角度重新审视生活中的名言名句，体现了数学作为人类文化结晶的特点，也使这节数学课融合了浓厚的文化气息。教学中，教师通过多媒体课件逐一展示名言名句，并配上与名言名句相匹配的图片背景，让学生探讨其中的充要关系，每个学生都踊跃发表看法，此时课堂学习的气氛再一次达到了高潮，再次激发了学生兴趣。

又如，在学习了比较实数大小的方法后，可设计这样的问题：为什么糖水中加的糖越多越甜？能否把它转化为数学问题。学生提出跟浓度有关，所以可转化为这样的数学问题，即a克糖水中含有b克糖(a〉b〉0)，则糖水的浓度为，若再加m(m〉0)克糖，此时糖水的浓度为，比较和的大小。这样不但加深巩固了对原有知识的理解，而且也大大激发了学生的探究兴趣。

心理学研究表明，兴趣是人对认识和活动的需要的情绪表现，是积极探究事物的认识倾向。学习兴趣是激发学习动机的首要条件，是学生学习最有活力的因素。因此，教师如能在教学中运用各种教学方法，培养学生的学习兴趣，就能变学生“要我学”为“我要学”，变学生被动学习为主动学习，使学生更好地投入到学习活动中去。

[1]李尚志.从数学中享受快乐[J].中学数学研究，2005，（3）. [2]王家聪.高中数学课堂教学结尾的设计[J].中学数学研究，2004，（4）.

[3]陈林.注重生活联系，激起学生学习数学的兴趣[J].科学教育家，2009，（4）.

G712

A

1672-5727（2010）10-0095-02

鲁军兵（1979—），男，浙江余姚人，余姚市职成教中心学校教师，中学二级教师，研究方向为职高数学教育。