非线性条件下砂土地基中水平受荷长桩的性状分析

夏唐代,王 梅,王志凯,胡文韬

(浙江大学 a.软弱土与环境土工教育部重点实验室;b.岩土工程研究所,杭州 310058)

近年来,承受水平荷载的超长竖直桩被广泛应用在海洋工程中,但是,水平受荷长桩的理论研究却不够完善,尤其是砂土地基中的水平受荷长桩,更少见研究。桩的水平荷载试验证明,水平荷载与桩挠度在挠度很小的阶段就呈非线性关系,当挠度继续增大,桩前土体会达到塑性屈服[1]。因此,只有考虑土体的非线性和塑性屈服,才能反映桩的真实性状,尤其是在靠船码头等容许桩发生较大位移的工程中,更应该考虑土体的塑性屈服,这是传统的m法做不到的,p-y曲线法虽然考虑了土体的非线性和塑性屈服,但是由于大多是基于试验所得,在缺乏必要的试验参数的情况下,很难被采用,而且,必须把地基土性质化为数学上的某种模型才能计算桩的性状,模型建立的不适当会给收敛计算带来很大麻烦。

基于以上的考虑,越来越多的学者开展了水平受荷单桩的非线性研究,力求建立一个合适的模型,既准确又方便计算。其中包括Behrouz[2]的有限元模型,吴锋[3]、王梅[4]等的试验研究,Wei Dong Guo[5-6]的理论分析等,均对桩的非线性研究有一定的指导意义,但是目前尚没有一个针对砂土地基,水平受荷长桩性状分析的合适模型。Prakash和Kumar[7]等通过研究Mwindo[8]的现场试验结果,总结出适合于砂土地基的水平土反力模量与地面处桩位移之间的非线性关系表达式,章连洋[9]应用该关系式分析了砂土地基中水平荷载作用下刚性桩的受力性状,计算值与实测值符合的较好。由于长桩与土相互作用的机理和破坏方式与短桩不同,章连洋的计算方法不适合长桩的计算,因此,该文在章连洋的基础上,研究了砂土地基中水平荷载作用下长桩的性状。计算模型中,假设水平土反力模量和极限土反力沿深度线性增长[9-10],土反力模量和桩位移之间是非线性关系,考虑桩前土体处于弹性和达到塑性屈服两种状态,分别建立桩的基本微分方程,由于涉及四阶变系数非线性微分方程的解答,数学上非常难解,该文给出了该方程的近似解答,由此可计算出沿桩身任一截面的位移和内力。算例证明,较m法计算准确,既适合桩体发生小位移的情况,也适合桩体发生较大位移的情况。又由于计算较 p-y曲线法方便可行,因此在缺乏实测参数的情况下,可代替p-y曲线法,用于工程实践。

1 分析方法

1.1 基本假定

1)桩是完全埋入砂土地基中的长桩,桩宽为B,长度为 L,弯曲刚度E P I P,桩顶自由,承受水平力 H 0和弯矩M 0,如图1(a)所示。

2)假定土反力模量kh沿深度线性增长[9-10],极限土反力pu沿深度线性增长Broms[11],如图1(b)、(c)所示。

图1

式中:nh为水平地基反力常数;m0为极限土反力沿深度线性增长的比例系数。

3)土反力p和桩位移y之间是非线性关系,随着y增大,p渐渐达到极限土反力pu,如图2所示。

图2 土反力和桩位移关系曲线

1.2 2种情况

基于以上假定,对长桩性状的分析分为 2种情况:

1)水平荷载较小,桩前土体仍处于弹性状态,如图3(a)所示。建立桩的挠度曲线微分方程:

结合地基反力法,令

式中:p(z,y)为单位桩长的土反力。

图3 土反力沿桩身的分布曲线

由式(1)、(3)、(4)得 :

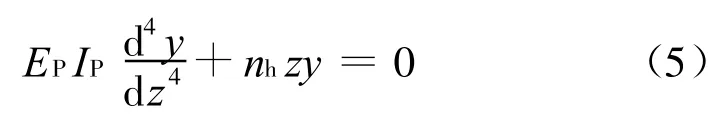
2)水平荷载足够大,使得桩前z0深度以上土体达到塑性屈服(对于长桩,不出现桩的全长范围内的水平向地基屈服[11]),如图3(b)所示。建立桩的挠度曲线微分方程:

由文献[11]

式中:KP为郎肯被动土压力系数;γ0为土的重度(为了和下文的剪应变符号γ区分,这里用γ0代表土的重度)。

分析桩的性状之前,必须先判断在给定的水平荷载下,桩前土体处于哪种状态,对于状态判断和2组方程的解法,将在第3节介绍。

1.3 水平土反力模量kh的非线性性质

在砂土地基中,假定水平土反力模量kh沿深度线性增长。由假定3可知,kh和y之间是非线性关系,k h随着y的增大而减小。许多学者研究了k h和y之间的关系,包括Bhushan et al[12],Mwindo[8],Kumar[13],Prakash和Kumar[7]等。基于现场试验,文献[12]提出了不同密实度的砂土地基中,n h和y0/B之间的关系,y 0是桩在地面处的位移,B是桩的宽度或桩径,基于文献 [7]、[8]、[13]、[14]的研究,文献[9]推导出nh(=kh/z)和 y0之间的非线性关系式:

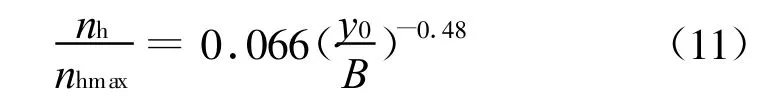
早在1955年,Terzaghi[10]提出了饱和与非饱和砂土的水平地基反力常数的取值范围,Reese[15-16]通过现场实验,修正了Terzaghi的建议值,Terzaghi、Reese对水平地基反力常数的取值可参考文献[9]中图4(Terzaghi和Reese所建议的水平地基反力常数的取值即相当于式(11)中的)。文献[7]等通过对文献[8]进行的砂土地基中14根单桩的现场实测资料进行分析,得到了适应于不同桩型不同密实度砂土地基中的值,并考虑到地下水位的影响(地下水位越低,n h值越大),提出了修正系数。后来文献[14]补充了14根单桩的实测资料,证实,在中密和密实砂土地基中,文献[7]对的建议值是合理的,而在松散砂土地基中,文献[7]对的建议取值范围略为宽泛,需进一步修正。文献[14]修正后的的取值见表1,关于地下水影响的修正系数,仍采用文献[7]的建议值(表2)。比较文献[9]中图4和本文中表1,可得,对于中密和密实砂土,文献[14]的建议值大于 Terzaghi、Reese的建议值,而对于松散砂土,文献[14]的建议值和Reese的很相近。研究证明 Terzaghi的建议值偏小[17],而Reese是建议值是基于两根桩的现场试验结果,缺乏普遍性,可能引起的误差也较大,因此该文建议选取文献[14]对于的建议值进行计算。

表1 水平地基反力常数nhmax的取值

表2 不同地下水位时nhmax的修正系数

1.4 长桩的判断

此文方法仅适用于长桩的计算,因此计算前需要判断是否属于长桩,首先计算桩土相对刚度系数T:

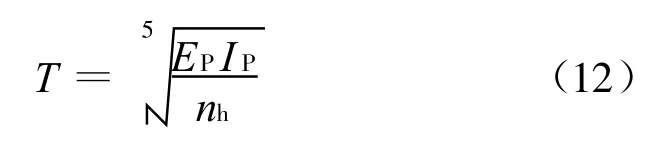
式中,nh可按照取值。

对于砂土地基中桩顶自由的单桩,当L≥4T时,可认为是长桩[17]。

2 四阶变系数非线性微分方程的解答

2.1 当桩前土体处于弹性状态时的计算

由式(5)、(11)得 :

式(17)等价于:

这是一个四阶变系数非线性微分方程,数学上很难得到其解析解,该文提出采用Gleser有限差分[1,18]结合迭代原理得到其近似解答。将桩平均分成n段,每段长为λ(λ=L/n),节点3代表桩顶节点,n+3代表桩端节点,沿桩顶向上延伸2个虚拟节点1、2,沿桩端向下延伸2个虚拟节点n+4,n+5。式(14)的近似解为

桩顶自由,将桩端视为自由端,得 4个边界条件:

由式(15)-(22)得递推公式:

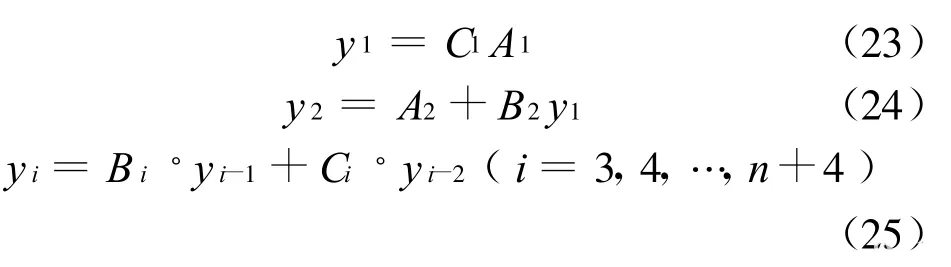
常规的Gleser法用于解四阶变系数微分方程时,要求kh i是常量,否则无法解答,但在该文中,kh i=f(y0)(y0即相当于桩顶节点的位移y3),而y0是未知的,为此,在常规Gleser法的基础上加入迭代程序,先给定一个初始的y0值,计算各节点的挠度yi,反复迭代计算,直到最后一次计算得到的y3与y0的相对误差在给定容许误差范围内时,即得实际的桩顶位移值y0。

为了避免y0初始值给定不当给计算带来的误差,建议根据Reese-Matlock法[1,7]对于给定水平荷载下桩在地面处位移的近似计算公式取值:

计算T时nh按照公式(11)取值。

下面给出程序计算桩身位移的步骤:

1)输入基本参数 n、L 、B 、E P I P、H0、M 0、n hmax、y0、ε;ε为预先设定的y0和y3之间的容许相对误差。

4)对于 i=n+1…4,3,循环计算出 Ci、Bi。

5)将式(21)代入上述过程,依次计算出B2、A2。

6)将式(22)代入上述过程,依次计算出C1、A1。

7)由式(23)-(25)依次计算 y1、y2、y3。

当yi(i=1,2…n+5)全部计算出后,可由式(31)～(34)计算桩身任一截面处的位移yi、转角θi、弯矩Mi、剪力Si和土反力pi:

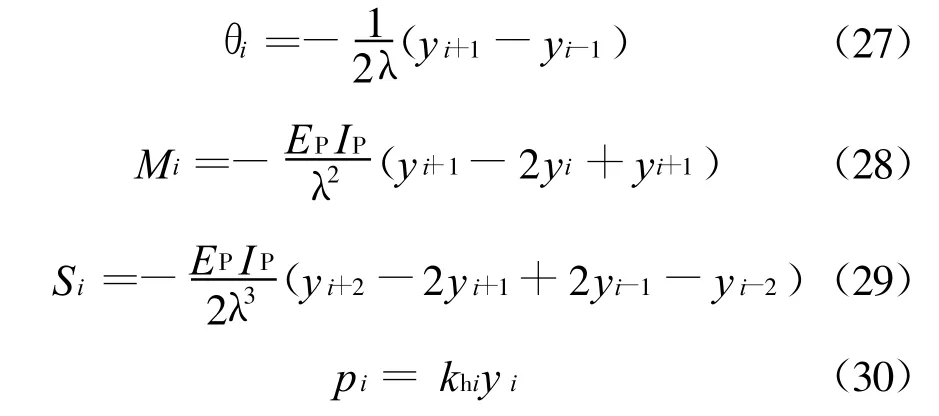
2.2 当桩前土体达到塑性屈服时的计算

在给定水平荷载下,首先判断桩前土体是否已经达到塑性屈服,由2.1的计算程序,可逐节点计算出 yi,对于每一个y i值,由式(30)计算得 pi,当 pi＞pu i(pu i为该节点处的极限土反力)时,证明土体已经达到屈服。

设塑性区深度z0,由式(6)-(8)、(11)得:

对于一个四阶常微分方程和一个变系数非线性四阶微分方程的联立解答,数学上未见算法,该文提出一种近似解法,可以计算出桩的性状。根据文献[11]的假设,设z0为桩身最大弯矩的位置,z0以上地基均达到屈服,z0以下仍为弹性,当桩顶水平荷载为 Ht时,则

将z0的位置假想为新的地面,z0以上土反力视作外荷载,设桩顶处位移 y0,假想地面处位移为yz0。对于式(34)的解答,由 Reese-Matlock法[1、7],有 :

式中:yz为假想地面以下深度z处桩身位移;Ay,By为深度系数,是z和y0的函数,可通过文献[1]查表求得近似值;

Hz0,Mz0为假想地面处作用的合力和合弯矩;

z=z0时:Ay0=2.43,By0=1.62,

由土反力连续条件:

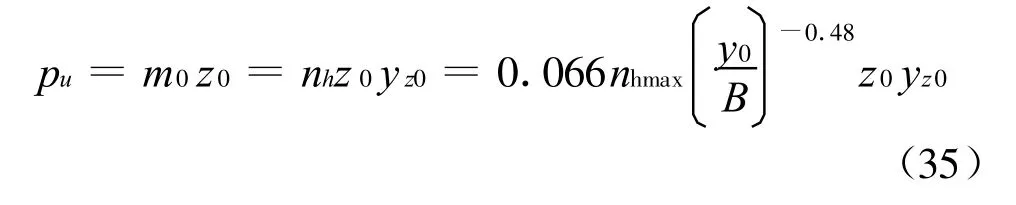
由(33)-(35),可解得z0,y0和 yz0,再加上桩顶边界条件 H=Ht,式(31)可解,因此,z0以上桩的内力可解,z0以下桩身内力计算,可参见文献[1]Reese-Matlock法。

3 算例分析

3.1 桩前土体处于弹性状态

扶余松花江大桥IV#试桩[19],地质条件:0～14 m,中砂,中密,饱和 ;14～ 17 m,粗砂 ,中密 ,饱和;17～21 m,砂质粘土,密实,半坚硬。桩的物理几何特征:钻孔灌注砼桩,有钢筋骨架,桩径B=1.62 m,桩长L=18.8 m。对桩顶分别施加300 kN、400 kN、500 kN、600 k N的水平力,地面处载荷比值e=由于是中密～密实砂土地基,由表 1,选取MN/m3,计算 T=2.69,L/T=6.99＞4,所以为长桩。由于没有给出土层的粘聚力c内摩擦角φ值,可按经验 ,取 c=0,φ=38°,γ0=20 k N/m3,地下水位于地表处,计算KP=3.85,m0=187。采用文中方法和传统的m法比较,对于m法,则取m×B=45 MN/m3(B为桩径)。计算时将桩划分为40个单元,计算出给定水平荷载下的桩顶位移和转角,当H0=600 kN,M0=150 kN◦m时,计算出了桩身弯矩分布,结果如图4-6所示。

图4 桩顶位移与水平荷载关系曲线

图5 桩顶转角与水平荷载关系曲线

图6 桩身弯矩随深度变化关系曲线(H0=600 k N)

由3.1的程序判断,在H 0=600 kN时,桩前土体仍处于弹性状态,但是当H0＞300 kN时,虽然桩顶最大位移仅有4.04 mm,土体已经表现出明显的非线性性质(图4-5),使用m法计算会有一定的误差,该文对于桩顶位移和转角,桩身弯矩的计算(图6)与实测值比较接近,比m法更精确。

3.2 桩前土体部分达到塑性屈服

文献[20]用“一维梁—柱有限单元”的数值解法计算了砂土地基中的钢筋混凝土钻孔灌注桩的性状。假设在给定荷载下,桩身一直保持线弹性工作状态,而桩前土体土反力和位移的关系服从Reese et al[15]的p-y曲线,即随着位移增大,土体由弹性达到塑性屈服。桩长 L=15 m,桩径 B=0.5 m,桩身弹性模量EP=41 000 MPa,砂土重度 γ0=18 kN/m3,有效内摩擦角=40°,文中给出 n hmax=17.5 MN/m3,对桩顶分别施加100～500 kN的水平力。计算E P IP≈0.126 GN◦m2,T=1.48,L/T=10＞4,所以为长桩。计算 KP=4.60,m0=3 KPγ0B=124,对 于 m 法,取 m ×B=17.5 MN/m3。计算时将桩划分为30个单元,计算出给定荷载下的桩顶位移,当H0=500 k N时,计算出了桩身弯矩分布,结果如图7-8所示。

图7 桩顶位移与水平荷载关系曲线

图8 桩身弯矩随深度变化关系曲线(H0=500 k N)

由文献[20]中采用的土体p-y曲线模型可知,在H0=160 kN时,桩前已产生塑性区;由该文3.1的程序判断,H0=250 k N时,桩前土体出现塑性区,两者的差别主要在于p-y曲线模型选取不同,文献[9]是以位移判断是否屈服,而此文是以土反力判断的,但是差别并不大,说明此文模型的合理性。同时说明,当 H0＞250 k N时,桩前一定存在塑性区。由图8可知,H0＜300 k N时,考虑土体塑性屈服和不考虑塑性屈服的计算位移几乎相同,这是因为塑性区范围较小,对于土体位移影响并不大;当H0＞400 kN时,不考虑塑性屈服的计算位移与文献[20]中计算值差别较大,而考虑土体塑性屈服的计算位移更接近文献[20]中计算值,更偏于安全,这是因为土体塑性区范围已经扩大,对于土体位移影响变大。由图8可知,考虑了土体塑性屈服的弯矩计算值更接近文献[20]中计算值。而同时可知,在这种桩顶发生较大位移的情况,土体表现出明显的非线性性质,m法计算的位移和弯矩远远小于数值计算值,不再适用。

4 结论

1)对于水平土反力模量的选取,考虑了土体的非线性性质,能更好地反映土体的实际受力性状。

2)考虑桩前土体处于弹性和达到塑性屈服2种状态,因此,既适用于小位移的情况,也适用于桩基容许出现大位移的情况,考虑土体塑性屈服的计算值比未考虑塑性屈服的更接近实测值,且偏于安全。

3)基本微分方程是四阶变系数非线性微分方程,该文给出了该方程的近似解答,使得计算方便可行。

4)算例证明,该方法较m法计算准确,较p-y曲线法计算方便,在缺乏实测参数的情况下,可代替p-y曲线法,用于工程实践。

5)水平反力地基常数n hmax的取值范围是基于有限试验资料所得,取值不合适会造成一定的计算误差,因此需对此进行进一步探讨。

[1]卢世深,林亚超.桩基础的计算和分析[M].北京:人民交通出版社,1987.

[2]BEHROUZ A,MOHAMMAD L.Pile-soil-structure interaction in pushover analysis of jacket offshore platforms using fiber elements[J].Constructional Steel Research,2009,65(1):209–18.

[3]吴锋,时蓓玲,卓杨.水平受荷桩非线性m法研究[J].岩土工程学报,2009,31(9):1398-1401.WU FENG,SHI BEI-LING,ZHUO YANG.Nonlinear‘m'method for piles under lateral load[J].Chinese Journal of Geotechnical Engineering,2009,31(9):1398-1401.

[4]王梅,楼志刚,李建乡,等.水平荷载作用下单桩非线性m法试验研究[J].岩土力学,2002,23(1):23–30.WANG MEI,LOU ZHI-GANG,LI JIAN-XIANG,ZHAO JING.Nonlinear analysis of‘m'method for single pile under lateral loading[J].Rock and Soil Mechanics,2002,23(1):23-30.

[5]WEI DONG GUO.Laterally loaded rigid piles in cohesionless soil[J].Canadian Geotechnical,2008,45(5):676-697.

[6]WEI DONG GUO.Nonlinear response of laterally loaded piles and pile groups[J].Numerical and Analytical Methods in Geomechanics,2008,33(7):879-914.

[7]PRAKASH S,K UMAR S.Nonlinear lateral pile deflection prediction in sands[J].Journal of Geotechnical Engineering,1996,122(2):130-138.

[8]MWINDO J M.Strain dependent soil modulus of horizontal subgrade reaction[D].University of Missouri,Rolla,MO.1992.

[9]ZHANG LIANYANG.Nonlinear analysis of laterally loaded rigid piles in cohesionless soil[J].Computers and Geotecnics,2009,36(5):718-724.

[10]TERZAGHI K.Evaluation of coefficients of subgrade reaction[J].Geotechnique,1955,5(4):297-326.

[11]BROMS B B.Lateral resistance of piles in cohesionless soils[J].Soil Mechanics and Foundations Division,1964,90(3):123-156.

[12]BHUSHAN K,LEE L J,GRIME D B.Lateral load tests on drilled piers in sand[C]//Proceedings of a session sponsored by the geotechnical engineering division and the ASCE national convention,Missouri,St.Louis,1981:114-31.

[13]KUMAR S.Non-linear load deflection prediction of single piles in sand using a subgrade reaction approach[D].University of Missouri,Rolla,MO.1993.

[14]KUMAR S,LALVANI L,OMAR M.Nonlinear response of single piles in sand subjected to lateral loads using khmaxapproach[J].Geotechnical and Geological Engineering,2006,24(1):163-81.

[15]REESE L C,COX W R,KOOP F D.Aanlysis of laterally loaded piles in sand[C]//Proceedings of 6 th offshore technical conference,Houston,Texas,1974,2:473-83.

[16]MEYER B J,REESE L C.Analysis of single piles under lateral loading,Research report No.244-1[R].Center for Transportation Research,The University of Texas,Austin,Texas;1979.

[17] TOMLINSON M J.Foundation design and construction.5th ed[M].London:Pitman Books Ltd.,1986.

[18]GLESER,SM.Lateral load tests on vertical fixed-hesd and free-head piles.[C]//Symposium on lateral load tests on piles,Special Technical Publication,1953,154:75-101.

[19]吴恒立.计算推力桩的综合刚度原理和双参数法[M].北京:人民交通出版社,1990.

[20]SUSHART L,KITTISAK K,ENRICO S.Response of reinforced concrete piles including soil-pile interaction effects[J].Engineering Structures,2009,31(9):1976-1986.